Question Number 13151 by Tinkutara last updated on 15/May/17

Answered by mrW1 last updated on 16/May/17

$${x}>\mathrm{9} \\ $$$$\mathrm{log}\:\left(\mathrm{2}{x}−\mathrm{1}\right)\left({x}−\mathrm{9}\right)>\mathrm{2} \\ $$$$\left(\mathrm{2}{x}−\mathrm{1}\right)\left({x}−\mathrm{9}\right)>\mathrm{100} \\ $$$$\mathrm{2}{x}^{\mathrm{2}} −\mathrm{19}{x}−\mathrm{91}>\mathrm{0} \\ $$$${x}_{\mathrm{1},\mathrm{2}} =\frac{\mathrm{19}\pm\sqrt{\mathrm{19}^{\mathrm{2}} +\mathrm{4}×\mathrm{2}×\mathrm{91}}}{\mathrm{4}}=\frac{\mathrm{19}\pm\mathrm{33}}{\mathrm{4}}=−\mathrm{3}.\mathrm{5}\:{or}\:\mathrm{13} \\ $$$$ \\ $$$$\Rightarrow{x}>\mathrm{13} \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 17/May/17

$${mrW}\mathrm{1}\:{is}\:{right}. \\ $$
Commented by Tinkutara last updated on 16/May/17
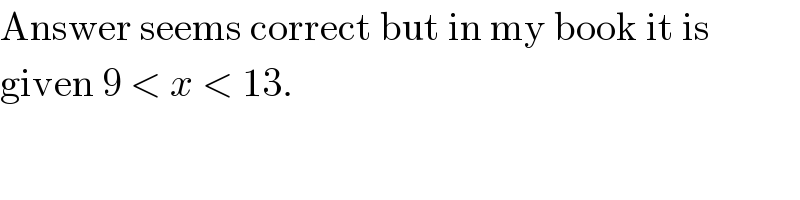
$$\mathrm{Answer}\:\mathrm{seems}\:\mathrm{correct}\:\mathrm{but}\:\mathrm{in}\:\mathrm{my}\:\mathrm{book}\:\mathrm{it}\:\mathrm{is}\: \\ $$$$\mathrm{given}\:\mathrm{9}\:<\:{x}\:<\:\mathrm{13}. \\ $$
Commented by Tinkutara last updated on 16/May/17

Commented by Tinkutara last updated on 16/May/17

$$\mathrm{Please}\:\mathrm{help}\:\mathrm{me}\:\mathrm{to}\:\mathrm{choose}\:\mathrm{the}\:\mathrm{correct} \\ $$$$\mathrm{answer}. \\ $$
Commented by mrW1 last updated on 16/May/17

$${The}\:{answer}\:{in}\:{your}\:{book}\:{is}\:{wrong}. \\ $$$${It}\:{were}\:{correct}\:{if}\:{the}\:{inequality}\:{is} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\mathrm{log}\:\left(\mathrm{2}{x}−\mathrm{1}\right)+\mathrm{log}\:\sqrt{{x}−\mathrm{9}}<\mathrm{1} \\ $$
Commented by Tinkutara last updated on 16/May/17

$$\mathrm{Thanks}.\:\mathrm{I}\:\mathrm{understood}. \\ $$
Commented by mrW1 last updated on 16/May/17

$${You}\:{can}\:{check}\:{with}\:{x}=\mathrm{10}, \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\mathrm{log}\:\left(\mathrm{2}×\mathrm{10}−\mathrm{1}\right)+\mathrm{log}\:\sqrt{\mathrm{10}−\mathrm{9}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{log}\:\left(\mathrm{19}\right)+\mathrm{log}\:\mathrm{1} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{log}\:\left(\mathrm{19}\right)<\frac{\mathrm{1}}{\mathrm{2}}\mathrm{log}\:\mathrm{100}=\mathrm{1} \\ $$$$ \\ $$$${with}\:{x}=\mathrm{20}, \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\mathrm{log}\:\left(\mathrm{2}×\mathrm{20}−\mathrm{1}\right)+\mathrm{log}\:\sqrt{\mathrm{20}−\mathrm{9}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{log}\:\left(\mathrm{39}\right)+\mathrm{log}\:\sqrt{\mathrm{11}} \\ $$$$>\frac{\mathrm{1}}{\mathrm{2}}\mathrm{log}\:\left(\mathrm{10}\right)+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{log}\:\mathrm{10}=\mathrm{1} \\ $$
Commented by Tinkutara last updated on 16/May/17

$$\mathrm{Thanks}\:\mathrm{very}\:\mathrm{much}! \\ $$
