Question Number 13194 by Tinkutara last updated on 16/May/17

Answered by ajfour last updated on 16/May/17
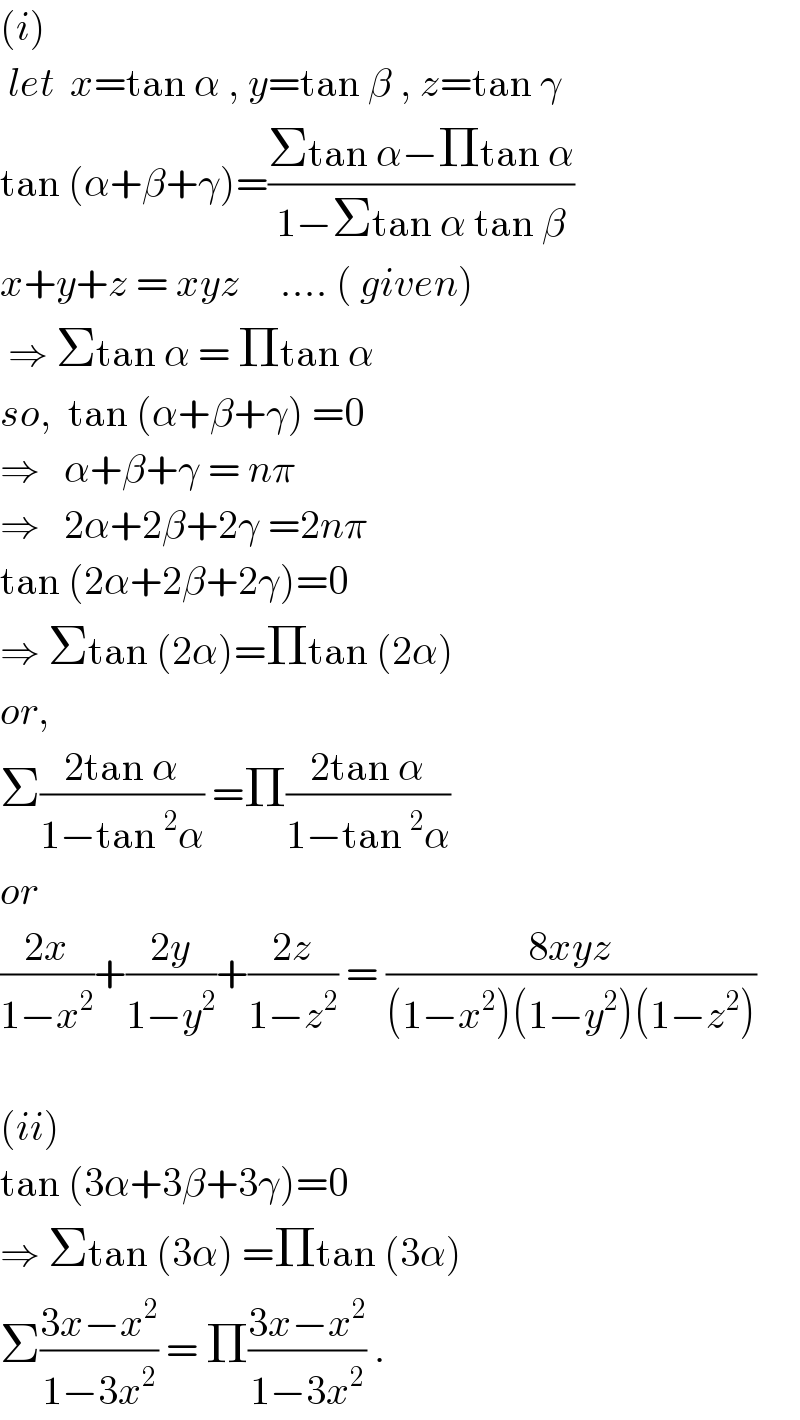
$$\left({i}\right)\: \\ $$$$\:{let}\:\:{x}=\mathrm{tan}\:\alpha\:,\:{y}=\mathrm{tan}\:\beta\:,\:{z}=\mathrm{tan}\:\gamma \\ $$$$\mathrm{tan}\:\left(\alpha+\beta+\gamma\right)=\frac{\Sigma\mathrm{tan}\:\alpha−\Pi\mathrm{tan}\:\alpha}{\mathrm{1}−\Sigma\mathrm{tan}\:\alpha\:\mathrm{tan}\:\beta} \\ $$$${x}+{y}+{z}\:=\:{xyz}\:\:\:\:\:….\:\left(\:{given}\right) \\ $$$$\:\Rightarrow\:\Sigma\mathrm{tan}\:\alpha\:=\:\Pi\mathrm{tan}\:\alpha\:\:\:\:\:\:\: \\ $$$${so},\:\:\mathrm{tan}\:\left(\alpha+\beta+\gamma\right)\:=\mathrm{0} \\ $$$$\Rightarrow\:\:\:\alpha+\beta+\gamma\:=\:{n}\pi \\ $$$$\Rightarrow\:\:\:\mathrm{2}\alpha+\mathrm{2}\beta+\mathrm{2}\gamma\:=\mathrm{2}{n}\pi \\ $$$$\mathrm{tan}\:\left(\mathrm{2}\alpha+\mathrm{2}\beta+\mathrm{2}\gamma\right)=\mathrm{0} \\ $$$$\Rightarrow\:\Sigma\mathrm{tan}\:\left(\mathrm{2}\alpha\right)=\Pi\mathrm{tan}\:\left(\mathrm{2}\alpha\right) \\ $$$${or}, \\ $$$$\Sigma\frac{\mathrm{2tan}\:\alpha}{\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} \alpha}\:=\Pi\frac{\mathrm{2tan}\:\alpha}{\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} \alpha} \\ $$$${or} \\ $$$$\frac{\mathrm{2}{x}}{\mathrm{1}−{x}^{\mathrm{2}} }+\frac{\mathrm{2}{y}}{\mathrm{1}−{y}^{\mathrm{2}} }+\frac{\mathrm{2}{z}}{\mathrm{1}−{z}^{\mathrm{2}} }\:=\:\frac{\mathrm{8}{xyz}}{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\left(\mathrm{1}−{y}^{\mathrm{2}} \right)\left(\mathrm{1}−{z}^{\mathrm{2}} \right)} \\ $$$$ \\ $$$$\left({ii}\right) \\ $$$$\mathrm{tan}\:\left(\mathrm{3}\alpha+\mathrm{3}\beta+\mathrm{3}\gamma\right)=\mathrm{0} \\ $$$$\Rightarrow\:\Sigma\mathrm{tan}\:\left(\mathrm{3}\alpha\right)\:=\Pi\mathrm{tan}\:\left(\mathrm{3}\alpha\right) \\ $$$$\Sigma\frac{\mathrm{3}{x}−{x}^{\mathrm{2}} }{\mathrm{1}−\mathrm{3}{x}^{\mathrm{2}} }\:=\:\Pi\frac{\mathrm{3}{x}−{x}^{\mathrm{2}} }{\mathrm{1}−\mathrm{3}{x}^{\mathrm{2}} }\:. \\ $$
Commented by Tinkutara last updated on 16/May/17

$$\mathrm{Thanks}\:\mathrm{a}\:\mathrm{lot}! \\ $$
