Menu Close

Question-13237

Tinku Tara 0 Comments
Pin




Question Number 13237 by Abbas-Nahi last updated on 17/May/17
Commented by RasheedSindhi last updated on 17/May/17
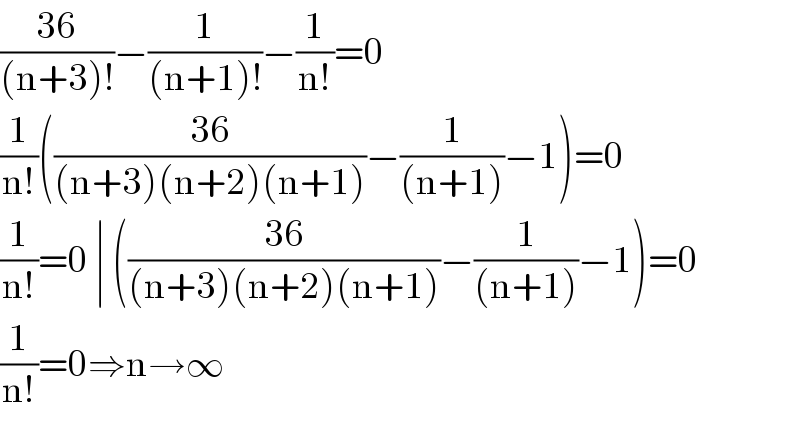
((36)/((n+3)!))−(1/((n+1)!))−(1/(n!))=0 (1/(n!))(((36)/((n+3)(n+2)(n+1)))−(1/((n+1)))−1)=0 (1/(n!))=0 ∣ (((36)/((n+3)(n+2)(n+1)))−(1/((n+1)))−1)=0 (1/(n!))=0⇒n→∞
$$\frac{\mathrm{36}}{\left(\mathrm{n}+\mathrm{3}\right)!}−\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)!}−\frac{\mathrm{1}}{\mathrm{n}!}=\mathrm{0} \\ $$$$\frac{\mathrm{1}}{\mathrm{n}!}\left(\frac{\mathrm{36}}{\left(\mathrm{n}+\mathrm{3}\right)\left(\mathrm{n}+\mathrm{2}\right)\left(\mathrm{n}+\mathrm{1}\right)}−\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\frac{\mathrm{1}}{\mathrm{n}!}=\mathrm{0}\:\mid\:\left(\frac{\mathrm{36}}{\left(\mathrm{n}+\mathrm{3}\right)\left(\mathrm{n}+\mathrm{2}\right)\left(\mathrm{n}+\mathrm{1}\right)}−\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\frac{\mathrm{1}}{\mathrm{n}!}=\mathrm{0}\Rightarrow\mathrm{n}\rightarrow\infty \\ $$
Commented by Abbas-Nahi last updated on 17/May/17
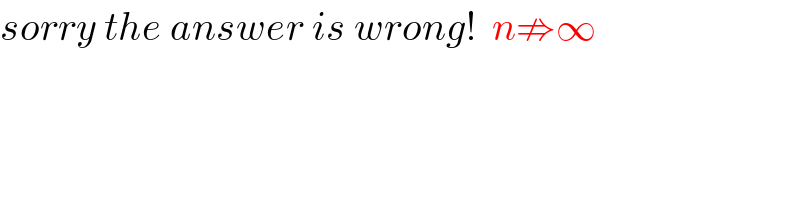
sorry the answer is wrong! n⇏∞
$${sorry}\:{the}\:{answer}\:{is}\:{wrong}!\:\:{n}\nRightarrow\infty \\ $$
Answered by RasheedSindhi last updated on 17/May/17
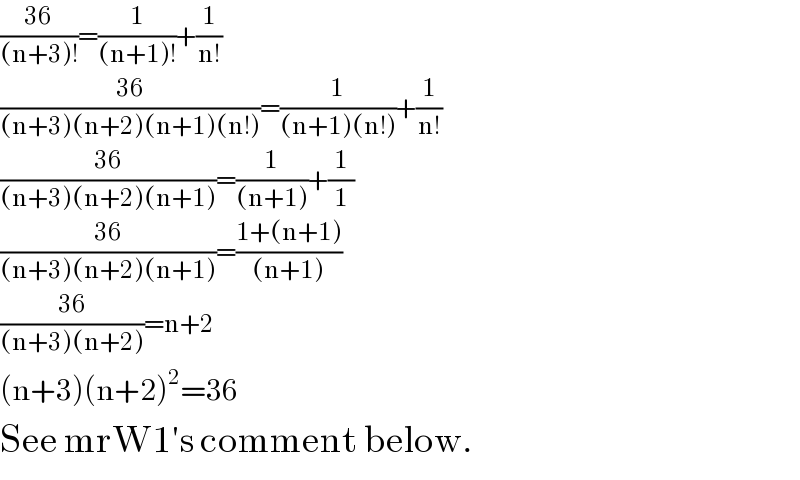
((36)/((n+3)!))=(1/((n+1)!))+(1/(n!)) ((36)/((n+3)(n+2)(n+1)(n!)))=(1/((n+1)(n!)))+(1/(n!)) ((36)/((n+3)(n+2)(n+1)))=(1/((n+1)))+(1/1) ((36)/((n+3)(n+2)(n+1)))=((1+(n+1))/((n+1))) ((36)/((n+3)(n+2)))=n+2 (n+3)(n+2)^2 =36 See mrW1′s comment below.
$$\frac{\mathrm{36}}{\left(\mathrm{n}+\mathrm{3}\right)!}=\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)!}+\frac{\mathrm{1}}{\mathrm{n}!} \\ $$$$\frac{\mathrm{36}}{\left(\mathrm{n}+\mathrm{3}\right)\left(\mathrm{n}+\mathrm{2}\right)\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{n}!\right)}=\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{n}!\right)}+\frac{\mathrm{1}}{\mathrm{n}!} \\ $$$$\frac{\mathrm{36}}{\left(\mathrm{n}+\mathrm{3}\right)\left(\mathrm{n}+\mathrm{2}\right)\left(\mathrm{n}+\mathrm{1}\right)}=\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)}+\frac{\mathrm{1}}{\mathrm{1}} \\ $$$$\frac{\mathrm{36}}{\left(\mathrm{n}+\mathrm{3}\right)\left(\mathrm{n}+\mathrm{2}\right)\left(\mathrm{n}+\mathrm{1}\right)}=\frac{\mathrm{1}+\left(\mathrm{n}+\mathrm{1}\right)}{\left(\mathrm{n}+\mathrm{1}\right)} \\ $$$$\frac{\mathrm{36}}{\left(\mathrm{n}+\mathrm{3}\right)\left(\mathrm{n}+\mathrm{2}\right)}=\mathrm{n}+\mathrm{2} \\ $$$$\left(\mathrm{n}+\mathrm{3}\right)\left(\mathrm{n}+\mathrm{2}\right)^{\mathrm{2}} =\mathrm{36} \\ $$$$\mathrm{See}\:\mathrm{mrW1}'\mathrm{s}\:\mathrm{comment}\:\mathrm{below}. \\ $$
Commented by mrW1 last updated on 17/May/17
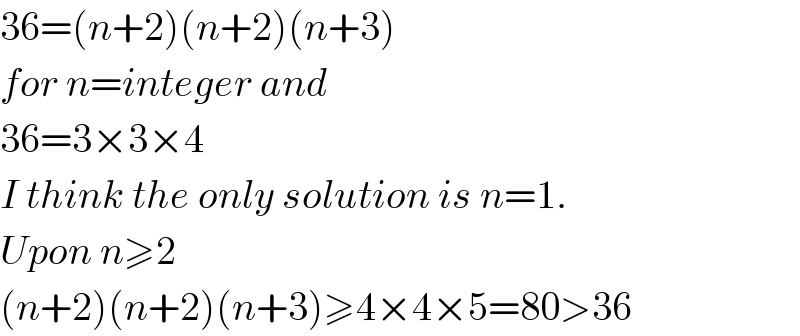
36=(n+2)(n+2)(n+3) for n=integer and 36=3×3×4 I think the only solution is n=1. Upon n≥2 (n+2)(n+2)(n+3)≥4×4×5=80>36
$$\mathrm{36}=\left({n}+\mathrm{2}\right)\left({n}+\mathrm{2}\right)\left({n}+\mathrm{3}\right) \\ $$$${for}\:{n}={integer}\:{and} \\ $$$$\mathrm{36}=\mathrm{3}×\mathrm{3}×\mathrm{4} \\ $$$${I}\:{think}\:{the}\:{only}\:{solution}\:{is}\:{n}=\mathrm{1}. \\ $$$${Upon}\:{n}\geqslant\mathrm{2} \\ $$$$\left({n}+\mathrm{2}\right)\left({n}+\mathrm{2}\right)\left({n}+\mathrm{3}\right)\geqslant\mathrm{4}×\mathrm{4}×\mathrm{5}=\mathrm{80}>\mathrm{36} \\ $$
Commented by Abbas-Nahi last updated on 17/May/17
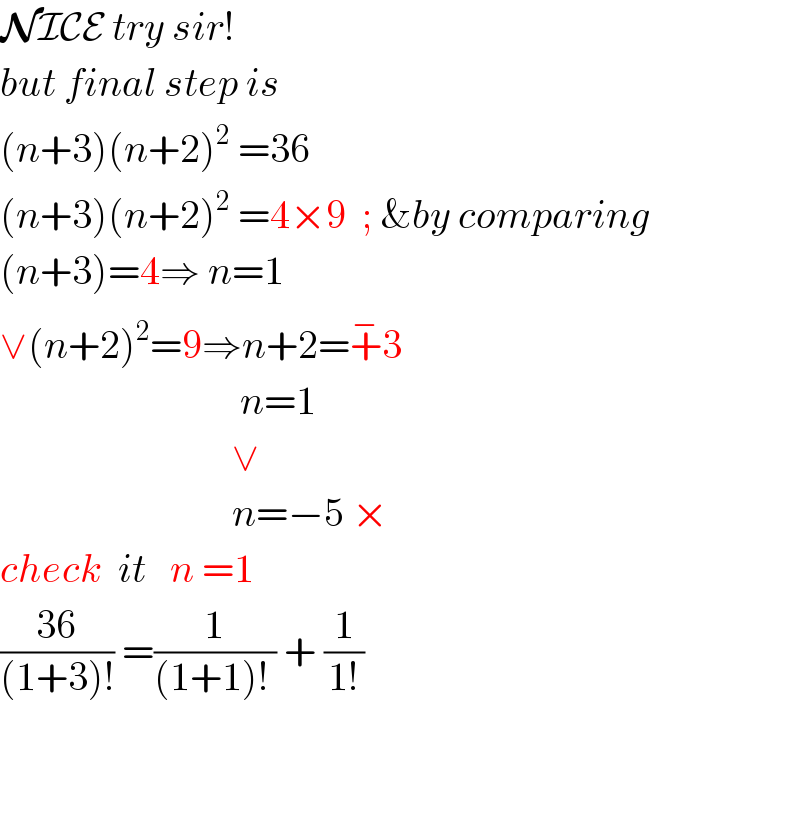
NICE try sir! but final step is (n+3)(n+2)^2 =36 (n+3)(n+2)^2 =4×9 ; &by comparing (n+3)=4⇒ n=1 ∨(n+2)^2 =9⇒n+2=+^− 3 n=1 ∨ n=−5 × check it n =1 ((36)/((1+3)!)) =(1/((1+1)! )) + (1/(1!))
$$\boldsymbol{\mathcal{N}}\mathcal{ICE}\:{try}\:{sir}!\: \\ $$$${but}\:{final}\:{step}\:{is} \\ $$$$\left({n}+\mathrm{3}\right)\left({n}+\mathrm{2}\right)^{\mathrm{2}} \:=\mathrm{36} \\ $$$$\left({n}+\mathrm{3}\right)\left({n}+\mathrm{2}\right)^{\mathrm{2}} \:=\mathrm{4}×\mathrm{9}\:\:;\:\&{by}\:{comparing} \\ $$$$\left({n}+\mathrm{3}\right)=\mathrm{4}\Rightarrow\:{n}=\mathrm{1} \\ $$$$\vee\left({n}+\mathrm{2}\right)^{\mathrm{2}} =\mathrm{9}\Rightarrow{n}+\mathrm{2}=\overset{−} {+}\mathrm{3} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{n}=\mathrm{1}\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\vee \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{n}=−\mathrm{5}\:× \\ $$$${check}\:\:{it}\:\:\:{n}\:=\mathrm{1} \\ $$$$\frac{\mathrm{36}}{\left(\mathrm{1}+\mathrm{3}\right)!}\:=\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{1}\right)!\:}\:+\:\frac{\mathrm{1}}{\mathrm{1}!} \\ $$$$ \\ $$$$ \\ $$
Commented by Abbas-Nahi last updated on 17/May/17
thank you sir!
$${thank}\:{you}\:{sir}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *