Question-13377

Question Number 13377 by tawa tawa last updated on 19/May/17

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 19/May/17

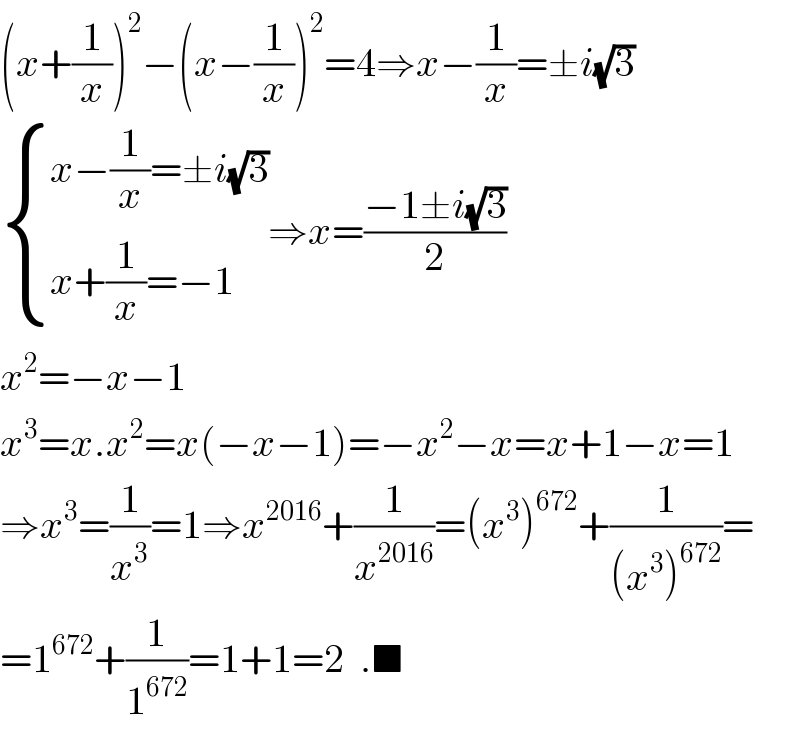
(x+(1/x))^2 −(x−(1/x))^2 =4⇒x−(1/x)=±i(√3) { ((x−(1/x)=±i(√3))),((x+(1/x)=−1)) :}⇒x=((−1±i(√3))/2) x^2 =−x−1 x^3 =x.x^2 =x(−x−1)=−x^2 −x=x+1−x=1 ⇒x^3 =(1/x^3 )=1⇒x^(2016) +(1/x^(2016) )=(x^3 )^(672) +(1/((x^3 )^(672) ))= =1^(672) +(1/1^(672) )=1+1=2 .■

$$\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} −\left({x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} =\mathrm{4}\Rightarrow{x}−\frac{\mathrm{1}}{{x}}=\pm{i}\sqrt{\mathrm{3}} \\ $$$$\begin{cases}{{x}−\frac{\mathrm{1}}{{x}}=\pm{i}\sqrt{\mathrm{3}}}\\{{x}+\frac{\mathrm{1}}{{x}}=−\mathrm{1}}\end{cases}\Rightarrow{x}=\frac{−\mathrm{1}\pm{i}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} =−{x}−\mathrm{1} \\ $$$${x}^{\mathrm{3}} ={x}.{x}^{\mathrm{2}} ={x}\left(−{x}−\mathrm{1}\right)=−{x}^{\mathrm{2}} −{x}={x}+\mathrm{1}−{x}=\mathrm{1} \\ $$$$\Rightarrow{x}^{\mathrm{3}} =\frac{\mathrm{1}}{{x}^{\mathrm{3}} }=\mathrm{1}\Rightarrow{x}^{\mathrm{2016}} +\frac{\mathrm{1}}{{x}^{\mathrm{2016}} }=\left({x}^{\mathrm{3}} \right)^{\mathrm{672}} +\frac{\mathrm{1}}{\left({x}^{\mathrm{3}} \right)^{\mathrm{672}} }= \\ $$$$=\mathrm{1}^{\mathrm{672}} +\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{672}} }=\mathrm{1}+\mathrm{1}=\mathrm{2}\:\:.\blacksquare \\ $$

Answered by ajfour last updated on 20/May/17

x+(1/x)=−1 ⇒ x^2 +x+1=0 x=((−1±(√(1−4)))/2) = −(1/2)±((i(√3))/2) =ω , ω^2 where (ω)^3 =1, (ω^2 )^3 =1 so x^(2016) =[(ω)^3 ]^(672) =1^(672) =1 hence x^(2016) +(1/x^(2016) ) = 1+1 =2 . (B)

$${x}+\frac{\mathrm{1}}{{x}}=−\mathrm{1} \\ $$$$\Rightarrow\:{x}^{\mathrm{2}} +{x}+\mathrm{1}=\mathrm{0} \\ $$$${x}=\frac{−\mathrm{1}\pm\sqrt{\mathrm{1}−\mathrm{4}}}{\mathrm{2}}\:=\:−\frac{\mathrm{1}}{\mathrm{2}}\pm\frac{{i}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\:\:=\omega\:,\:\omega^{\mathrm{2}} \:{where}\:\:\left(\omega\right)^{\mathrm{3}} =\mathrm{1},\:\left(\omega^{\mathrm{2}} \right)^{\mathrm{3}} =\mathrm{1} \\ $$$${so}\:{x}^{\mathrm{2016}} =\left[\left(\omega\right)^{\mathrm{3}} \right]^{\mathrm{672}} =\mathrm{1}^{\mathrm{672}} =\mathrm{1} \\ $$$${hence} \\ $$$${x}^{\mathrm{2016}} +\frac{\mathrm{1}}{{x}^{\mathrm{2016}} }\:=\:\mathrm{1}+\mathrm{1}\:=\mathrm{2}\:\:.\:\:\:\left({B}\right) \\ $$

Commented by prakash jain last updated on 20/May/17

Please check x=±ω? I think it should be x=ω,ω^2 Also (±ω)^3 ≠1 ω^3 =1,(−ω)^3 =−ω^3 =−1

$$\mathrm{Please}\:\mathrm{check} \\ $$$${x}=\pm\omega? \\ $$$$\mathrm{I}\:\mathrm{think}\:\mathrm{it}\:\mathrm{should}\:\mathrm{be} \\ $$$${x}=\omega,\omega^{\mathrm{2}} \\ $$$$\mathrm{Also}\:\left(\pm\omega\right)^{\mathrm{3}} \neq\mathrm{1} \\ $$$$\omega^{\mathrm{3}} =\mathrm{1},\left(−\omega\right)^{\mathrm{3}} =−\omega^{\mathrm{3}} =−\mathrm{1} \\ $$

Commented by FilupS last updated on 20/May/17

what is ω? I′ve never seen the notation (±ω)^3 =1

$$\mathrm{what}\:\mathrm{is}\:\omega? \\ $$$$\mathrm{I}'\mathrm{ve}\:\mathrm{never}\:\mathrm{seen}\:\mathrm{the}\:\mathrm{notation}\:\left(\pm\omega\right)^{\mathrm{3}} =\mathrm{1} \\ $$

Commented by ajfour last updated on 20/May/17

$${thanks}\:,\:{i}'{ve}\:{corrected}\:. \\ $$

Commented by prakash jain last updated on 20/May/17

Filup, 1,ω,ω^2 are cube roots of unity. or 3 solutions of equation x^3 =1⇒(x−1)(1+x+x^2 )=0 x=1, 1+x+x^2 =0 has 2 roots (ω,ω^2 ) as in answer above. w,w^2 =−(1/2)±((i(√3))/2)

$$\mathrm{Filup}, \\ $$$$\mathrm{1},\omega,\omega^{\mathrm{2}} \:\mathrm{are}\:\mathrm{cube}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{unity}. \\ $$$$\mathrm{or}\:\mathrm{3}\:\mathrm{solutions}\:\mathrm{of}\:\mathrm{equation} \\ $$$${x}^{\mathrm{3}} =\mathrm{1}\Rightarrow\left({x}−\mathrm{1}\right)\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$${x}=\mathrm{1},\:\mathrm{1}+{x}+{x}^{\mathrm{2}} =\mathrm{0}\:\mathrm{has}\:\mathrm{2}\:\mathrm{roots}\:\left(\omega,\omega^{\mathrm{2}} \right) \\ $$$$\mathrm{as}\:\mathrm{in}\:\mathrm{answer}\:\mathrm{above}. \\ $$$${w},{w}^{\mathrm{2}} =−\frac{\mathrm{1}}{\mathrm{2}}\pm\frac{{i}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply