Menu Close

Question-13544

Tinku Tara 0 Comments
Pin




Question Number 13544 by aishadenge last updated on 20/May/17
Commented by prakash jain last updated on 20/May/17
What is z?
$$\mathrm{What}\:\mathrm{is}\:{z}? \\ $$
Commented by aishadenge last updated on 20/May/17
the top part is equated to z not x. sorry for the error.
$${the}\:{top}\:{part}\:{is}\:{equated}\:{to}\:{z}\:{not}\:{x}.\:{sorry}\: \\ $$$${for}\:{the}\:{error}. \\ $$
Commented by prakash jain last updated on 21/May/17
(∂z/∂x)=e^(−x) (∂/∂x)(ycos x+ysin y) +(ycos x+ysin y)(∂/∂x)e^(−x) =e^(−x) (−ysin x)−e^(−x) (ycos x+ysin y) =−ye^(−x) (cos x+sin x+sin y) (∂^2 z/∂x^2 )=−ye^(−x) (∂/∂x)(cos x+sin x+sin y) −y(cos x+sin x+sin y)(∂/∂x)e^(−x) =−ye^(−x) (−sin x+cos x)+ye^(−x) (cos x+sin x+sin y) =ye^(−x) (sin y+2sin x) (∂z/∂y)=e^(−x) (cos x+sin y+ycos y) (∂^2 z/∂y^2 )=e^(−x) (cos y+cos y−ysin y) (∂^2 z/∂x^2 )+(∂^2 z/∂y^2 )≠0 Please recheck question. I will also recheck answer.
$$\frac{\partial{z}}{\partial{x}}={e}^{−{x}} \frac{\partial}{\partial{x}}\left({y}\mathrm{cos}\:{x}+{y}\mathrm{sin}\:{y}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:+\left({y}\mathrm{cos}\:{x}+{y}\mathrm{sin}\:{y}\right)\frac{\partial}{\partial{x}}{e}^{−{x}} \\ $$$$={e}^{−{x}} \left(−{y}\mathrm{sin}\:{x}\right)−{e}^{−{x}} \left({y}\mathrm{cos}\:{x}+{y}\mathrm{sin}\:{y}\right) \\ $$$$=−{ye}^{−{x}} \left(\mathrm{cos}\:{x}+\mathrm{sin}\:{x}+\mathrm{sin}\:{y}\right) \\ $$$$\frac{\partial^{\mathrm{2}} {z}}{\partial{x}^{\mathrm{2}} }=−{ye}^{−{x}} \frac{\partial}{\partial{x}}\left(\mathrm{cos}\:{x}+\mathrm{sin}\:{x}+\mathrm{sin}\:{y}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−{y}\left(\mathrm{cos}\:{x}+\mathrm{sin}\:{x}+\mathrm{sin}\:{y}\right)\frac{\partial}{\partial{x}}{e}^{−{x}} \\ $$$$=−{ye}^{−{x}} \left(−\mathrm{sin}\:{x}+\mathrm{cos}\:{x}\right)+{ye}^{−{x}} \left(\mathrm{cos}\:{x}+\mathrm{sin}\:{x}+\mathrm{sin}\:{y}\right) \\ $$$$={ye}^{−{x}} \left(\mathrm{sin}\:{y}+\mathrm{2sin}\:{x}\right) \\ $$$$ \\ $$$$\frac{\partial{z}}{\partial{y}}={e}^{−{x}} \left(\mathrm{cos}\:{x}+\mathrm{sin}\:{y}+{y}\mathrm{cos}\:{y}\right) \\ $$$$\frac{\partial^{\mathrm{2}} {z}}{\partial{y}^{\mathrm{2}} }={e}^{−{x}} \left(\mathrm{cos}\:{y}+\mathrm{cos}\:{y}−{y}\mathrm{sin}\:{y}\right) \\ $$$$\frac{\partial^{\mathrm{2}} {z}}{\partial{x}^{\mathrm{2}} }+\frac{\partial^{\mathrm{2}} {z}}{\partial{y}^{\mathrm{2}} }\neq\mathrm{0} \\ $$$$\mathrm{Please}\:\mathrm{recheck}\:\mathrm{question}. \\ $$$$\mathrm{I}\:\mathrm{will}\:\mathrm{also}\:\mathrm{recheck}\:\mathrm{answer}. \\ $$
Commented by mrW1 last updated on 21/May/17
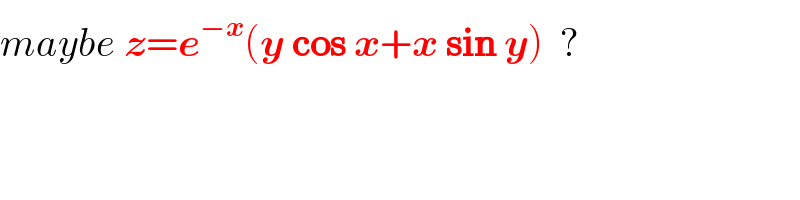
maybe z=e^(−x) (y cos x+x sin y) ?
$${maybe}\:\boldsymbol{{z}}=\boldsymbol{{e}}^{−\boldsymbol{{x}}} \left(\boldsymbol{{y}}\:\boldsymbol{\mathrm{cos}}\:\boldsymbol{{x}}+\boldsymbol{{x}}\:\boldsymbol{\mathrm{sin}}\:\boldsymbol{{y}}\right)\:\:? \\ $$
Commented by aishadenge last updated on 21/May/17
thank you.
$${thank}\:{you}. \\ $$
Commented by aishadenge last updated on 21/May/17
i checked. it is ycosx+xsiny indeed
$${i}\:{checked}.\:{it}\:{is}\:\boldsymbol{{ycosx}}+\boldsymbol{{xsiny}}\:\:\:{indeed} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *