Menu Close

Question-13548

Tinku Tara 0 Comments
Pin




Question Number 13548 by b.e.h.i.8.3.4.1.7@gmail.com last updated on 20/May/17
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 22/May/17
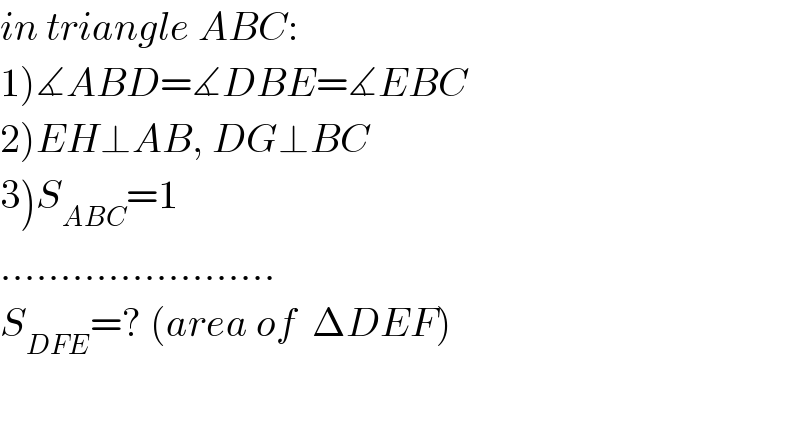
in triangle ABC: 1)∡ABD=∡DBE=∡EBC 2)EH⊥AB, DG⊥BC 3)S_(ABC) =1 ....................... S_(DFE) =? (area of ΔDEF)
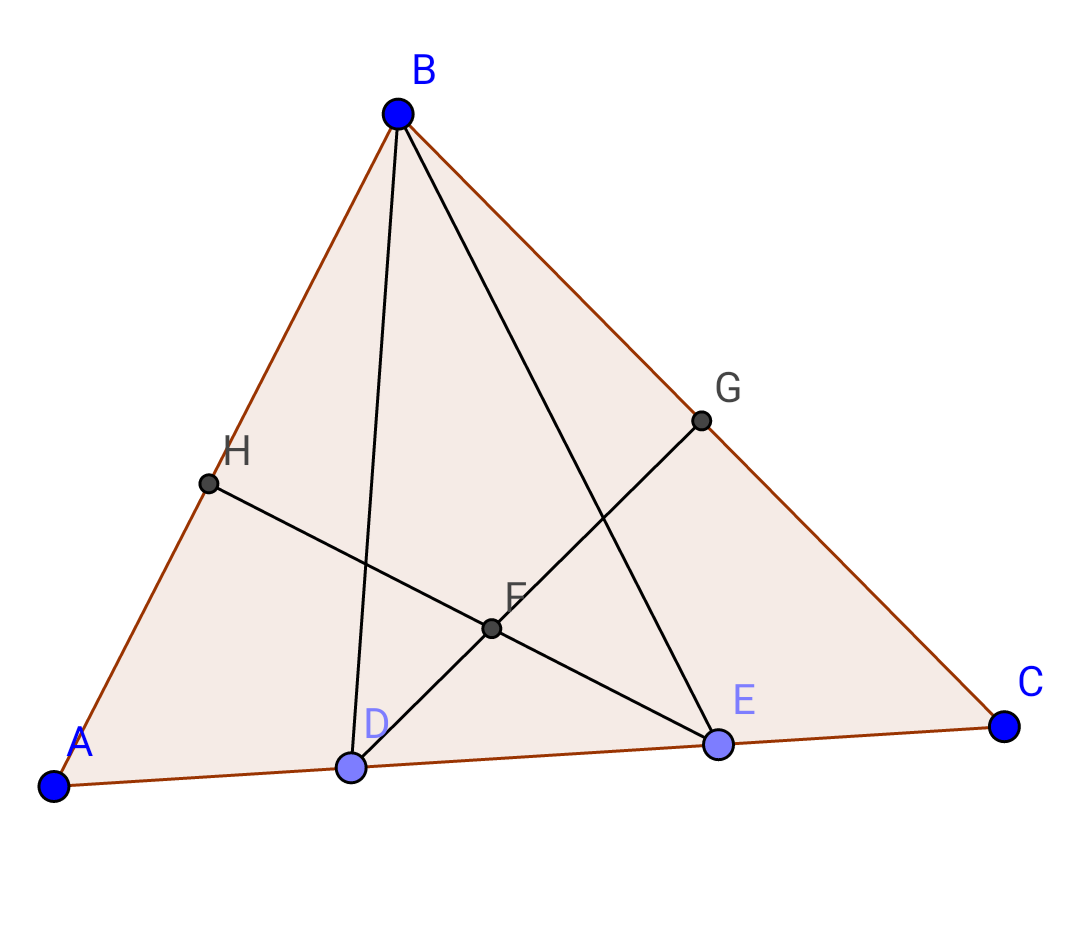
$${in}\:{triangle}\:{ABC}: \\ $$$$\left.\mathrm{1}\right)\measuredangle{ABD}=\measuredangle{DBE}=\measuredangle{EBC} \\ $$$$\left.\mathrm{2}\right){EH}\bot{AB},\:{DG}\bot{BC} \\ $$$$\left.\mathrm{3}\right){S}_{{ABC}} =\mathrm{1} \\ $$$$………………….. \\ $$$${S}_{{DFE}} =?\:\left({area}\:{of}\:\:\Delta{DEF}\right) \\ $$$$ \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 20/May/17
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 20/May/17
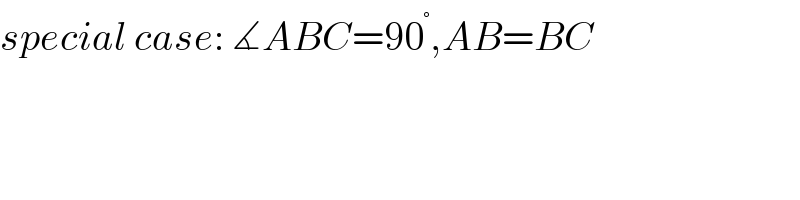
special case: ∡ABC=90^° ,AB=BC
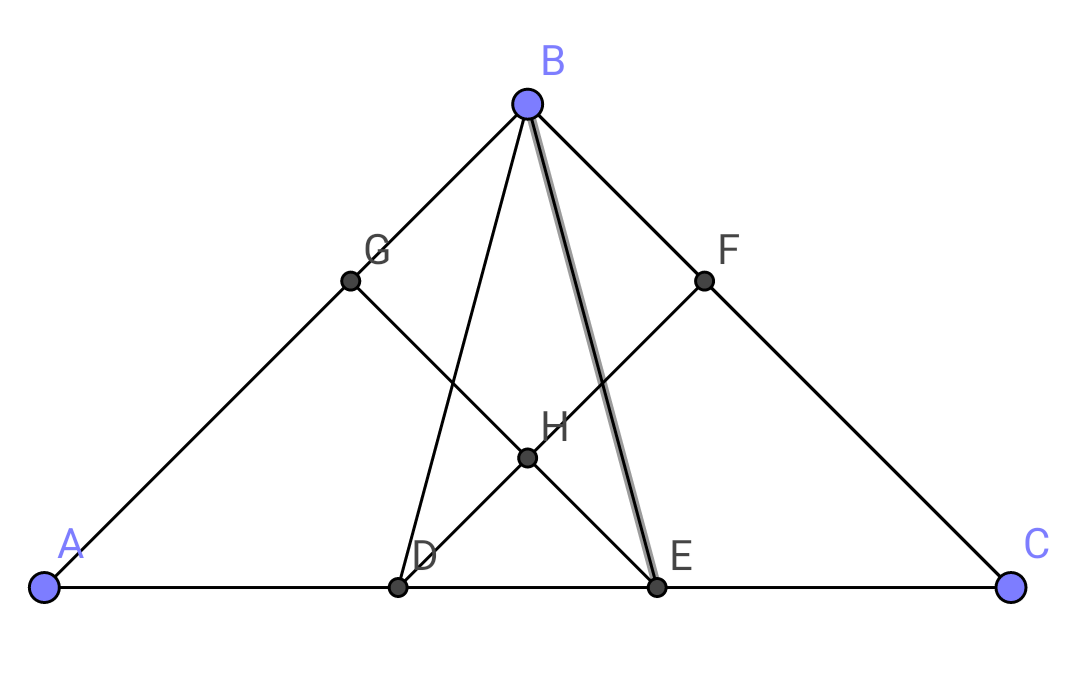
$${special}\:{case}:\:\measuredangle{ABC}=\mathrm{90}^{°} ,{AB}={BC} \\ $$
Commented by mrW1 last updated on 21/May/17
I don′t think (S_(DFE) /S_(ABC) )=constant. According to the 3 conditions we can not determine S_(DFE) . See picture: Both cases have the same conditions, but S_(DFE) is not the same.
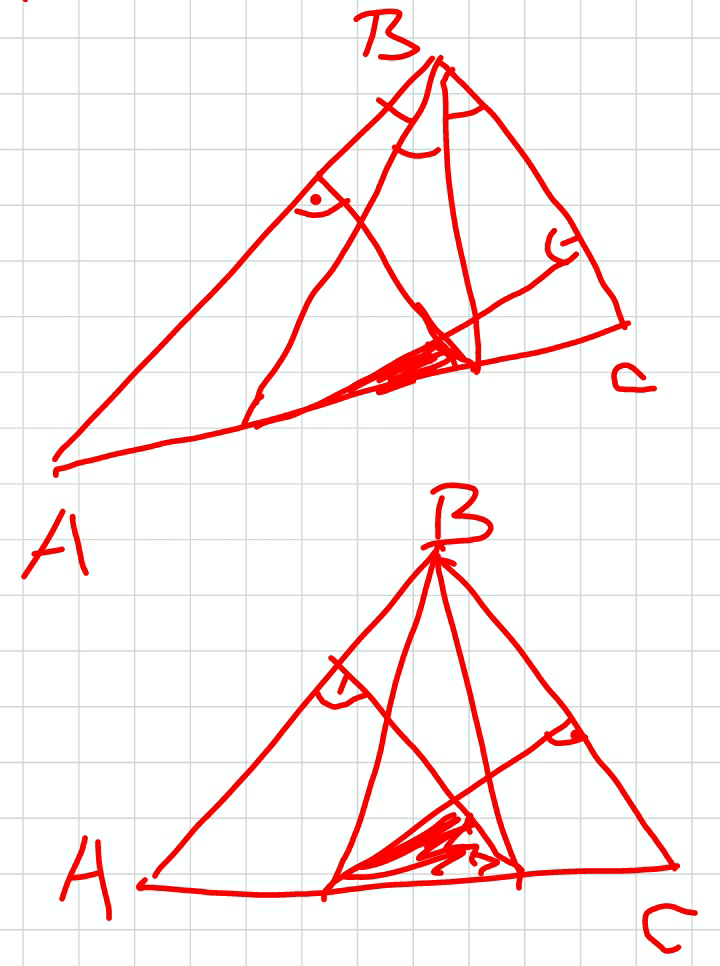
$${I}\:{don}'{t}\:{think}\:\frac{{S}_{{DFE}} }{{S}_{{ABC}} }={constant}. \\ $$$${According}\:{to}\:{the}\:\mathrm{3}\:{conditions}\:{we} \\ $$$${can}\:{not}\:{determine}\:{S}_{{DFE}} . \\ $$$$ \\ $$$${See}\:{picture}: \\ $$$${Both}\:{cases}\:{have}\:{the}\:{same}\:{conditions}, \\ $$$${but}\:{S}_{{DFE}} \:{is}\:{not}\:{the}\:{same}. \\ $$
Commented by mrW1 last updated on 21/May/17
Commented by mrW1 last updated on 21/May/17
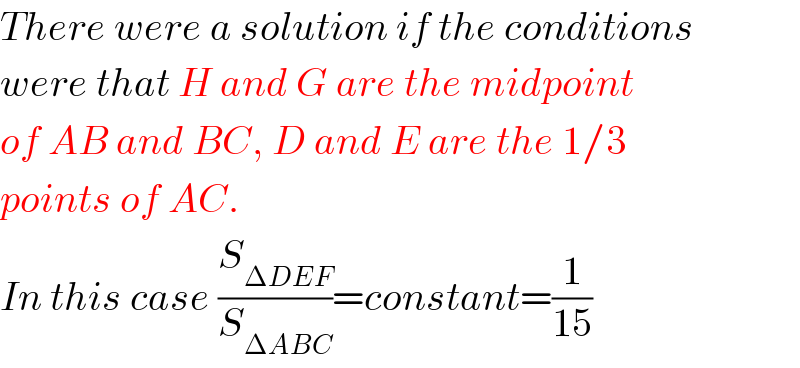
There were a solution if the conditions were that H and G are the midpoint of AB and BC, D and E are the 1/3 points of AC. In this case (S_(ΔDEF) /S_(ΔABC) )=constant=(1/(15))
$${There}\:{were}\:{a}\:{solution}\:{if}\:{the}\:{conditions} \\ $$$${were}\:{that}\:{H}\:{and}\:{G}\:{are}\:{the}\:{midpoint} \\ $$$${of}\:{AB}\:{and}\:{BC},\:{D}\:{and}\:{E}\:{are}\:{the}\:\mathrm{1}/\mathrm{3}\: \\ $$$${points}\:{of}\:{AC}. \\ $$$${In}\:{this}\:{case}\:\frac{{S}_{\Delta{DEF}} }{{S}_{\Delta{ABC}} }={constant}=\frac{\mathrm{1}}{\mathrm{15}} \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 21/May/17
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 21/May/17
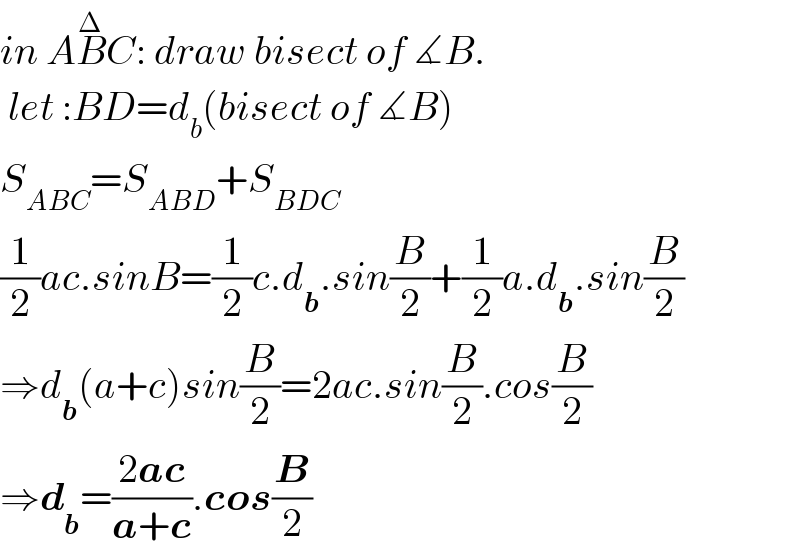
in AB^Δ C^ : draw bisect of ∡B. let :BD=d_b (bisect of ∡B) S_(ABC) =S_(ABD) +S_(BDC) (1/2)ac.sinB=(1/2)c.d_b .sin(B/2)+(1/2)a.d_b .sin(B/2) ⇒d_b (a+c)sin(B/2)=2ac.sin(B/2).cos(B/2) ⇒d_b =((2ac)/(a+c)).cos(B/2)
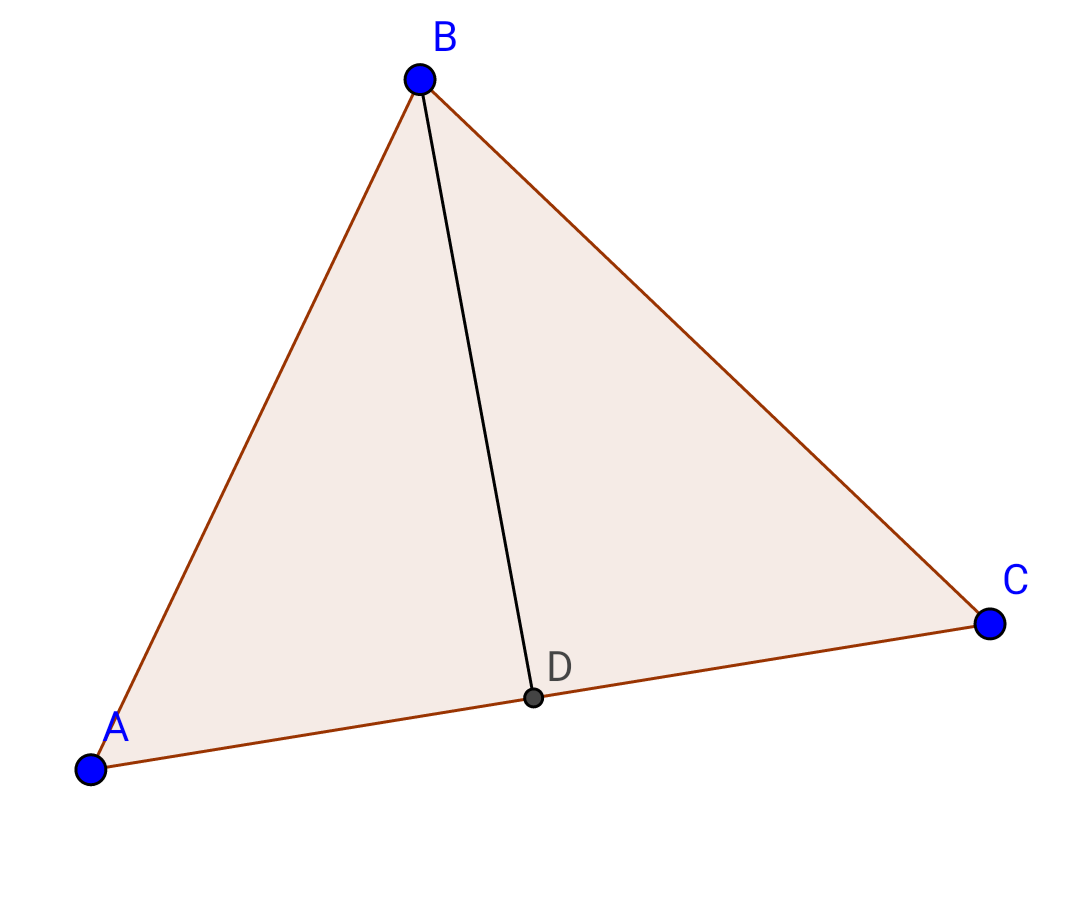
$${in}\:{A}\overset{\Delta} {{B}}\overset{} {{C}}:\:{draw}\:{bisect}\:{of}\:\measuredangle{B}. \\ $$$$\:{let}\::{BD}={d}_{{b}} \left({bisect}\:{of}\:\measuredangle{B}\right) \\ $$$${S}_{{ABC}} ={S}_{{ABD}} +{S}_{{BDC}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{ac}.{sinB}=\frac{\mathrm{1}}{\mathrm{2}}{c}.{d}_{\boldsymbol{{b}}} .{sin}\frac{{B}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}{a}.{d}_{\boldsymbol{{b}}} .{sin}\frac{{B}}{\mathrm{2}} \\ $$$$\Rightarrow{d}_{\boldsymbol{{b}}} \left({a}+{c}\right){sin}\frac{{B}}{\mathrm{2}}=\mathrm{2}{ac}.{sin}\frac{{B}}{\mathrm{2}}.{cos}\frac{{B}}{\mathrm{2}} \\ $$$$\Rightarrow\boldsymbol{{d}}_{\boldsymbol{{b}}} =\frac{\mathrm{2}\boldsymbol{{ac}}}{\boldsymbol{{a}}+\boldsymbol{{c}}}.\boldsymbol{{cos}}\frac{\boldsymbol{{B}}}{\mathrm{2}} \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 21/May/17
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 22/May/17
in trianvle:AB^Δ C^ ,draw trisect of∡B. now:∡ABE=∡EBF=∡FBC=((∡B)/3) let:BE=d_1 ,BF=d_2 from the commenet above,in AB^Δ F, BE is bisect of ∡ABF,so we have: d_1 =((2ad_2 )/(a+d_2 ))cos(B/3),similarly:d_2 =((2cd_1 )/(c+d_1 ))cos(B/3) { ((ad_1 +d_1 d_2 =2ad_2 .cos(B/3))),((cd_2 +d_1 d_2 =2cd_1 .cos(B/3))) :}from this system: { ((d_1 =((ac)/(c+2a.cos(B/3)))(4cos^2 (B/3)−1))),((d_2 =((ac)/(a+2c.cos(B/3)))(4cos^2 (B/3)−1))) :}
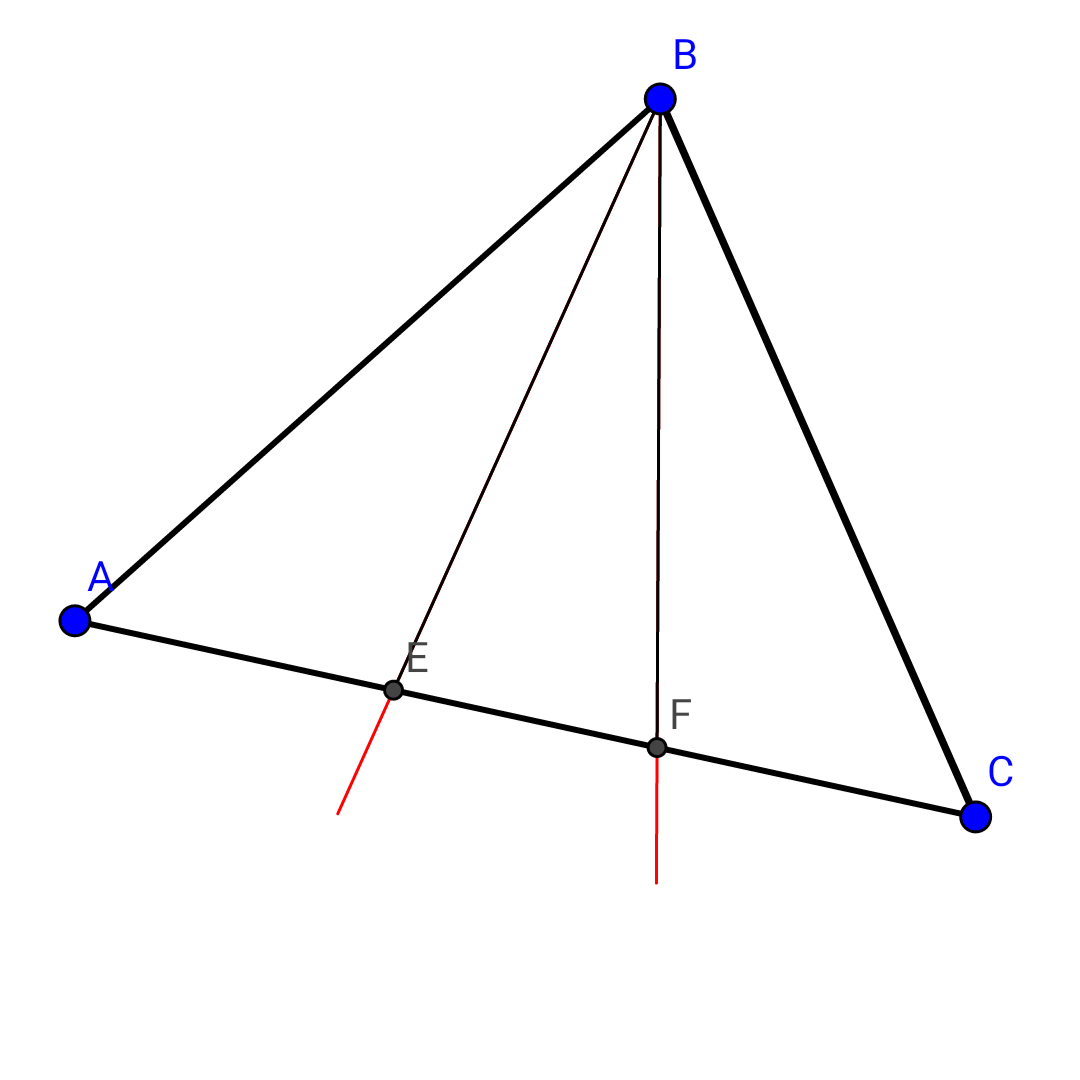
$${in}\:{trianvle}:{A}\overset{\Delta} {{B}}\overset{} {{C}},{draw}\:{trisect}\:{of}\measuredangle{B}. \\ $$$${now}:\measuredangle{ABE}=\measuredangle{EBF}=\measuredangle{FBC}=\frac{\measuredangle{B}}{\mathrm{3}} \\ $$$${let}:{BE}={d}_{\mathrm{1}} ,{BF}={d}_{\mathrm{2}} \\ $$$${from}\:{the}\:{commenet}\:{above},{in}\:{A}\overset{\Delta} {{B}F}, \\ $$$${BE}\:{is}\:{bisect}\:{of}\:\measuredangle{ABF},{so}\:{we}\:{have}: \\ $$$${d}_{\mathrm{1}} =\frac{\mathrm{2}{ad}_{\mathrm{2}} }{{a}+{d}_{\mathrm{2}} }{cos}\frac{{B}}{\mathrm{3}},{similarly}:{d}_{\mathrm{2}} =\frac{\mathrm{2}{cd}_{\mathrm{1}} }{{c}+{d}_{\mathrm{1}} }{cos}\frac{{B}}{\mathrm{3}} \\ $$$$\begin{cases}{\boldsymbol{{ad}}_{\mathrm{1}} +\boldsymbol{{d}}_{\mathrm{1}} \boldsymbol{{d}}_{\mathrm{2}} =\mathrm{2}\boldsymbol{{ad}}_{\mathrm{2}} .\boldsymbol{{cos}}\frac{\boldsymbol{{B}}}{\mathrm{3}}}\\{\boldsymbol{{cd}}_{\mathrm{2}} +\boldsymbol{{d}}_{\mathrm{1}} \boldsymbol{{d}}_{\mathrm{2}} =\mathrm{2}\boldsymbol{{cd}}_{\mathrm{1}} .\boldsymbol{{cos}}\frac{\boldsymbol{{B}}}{\mathrm{3}}}\end{cases}{from}\:{this}\:{system}: \\ $$$$\begin{cases}{\boldsymbol{{d}}_{\mathrm{1}} =\frac{\boldsymbol{{ac}}}{\boldsymbol{{c}}+\mathrm{2}\boldsymbol{{a}}.\boldsymbol{{cos}}\frac{\boldsymbol{{B}}}{\mathrm{3}}}\left(\mathrm{4}\boldsymbol{{cos}}^{\mathrm{2}} \frac{\boldsymbol{{B}}}{\mathrm{3}}−\mathrm{1}\right)}\\{\boldsymbol{{d}}_{\mathrm{2}} =\frac{\boldsymbol{{ac}}}{\boldsymbol{{a}}+\mathrm{2}\boldsymbol{{c}}.\boldsymbol{{cos}}\frac{\boldsymbol{{B}}}{\mathrm{3}}}\left(\mathrm{4}\boldsymbol{{cos}}^{\mathrm{2}} \frac{\boldsymbol{{B}}}{\mathrm{3}}−\mathrm{1}\right)}\end{cases} \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 22/May/17
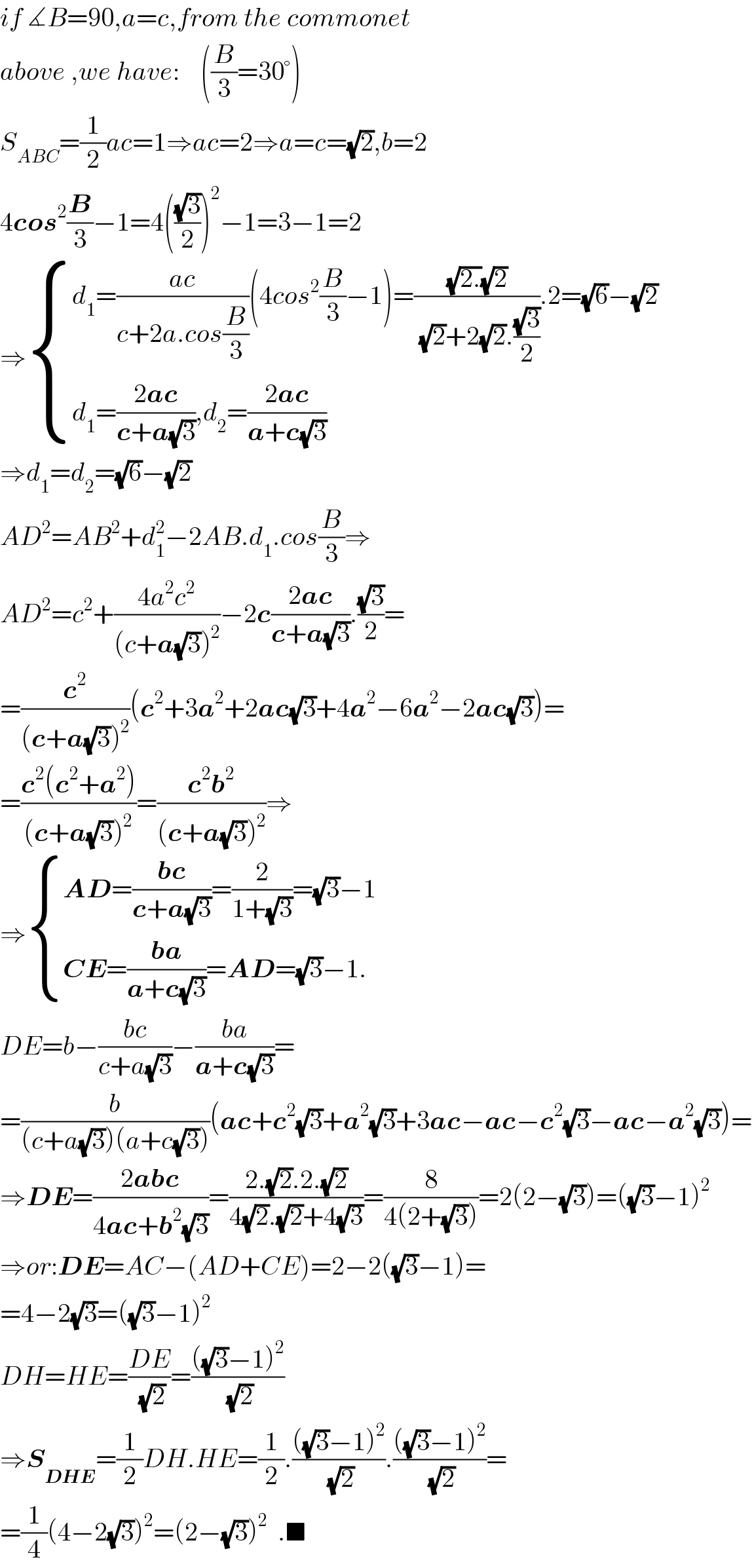
if ∡B=90,a=c,from the commonet above ,we have: ((B/3)=30°) S_(ABC) =(1/2)ac=1⇒ac=2⇒a=c=(√2),b=2 4cos^2 (B/3)−1=4(((√3)/2))^2 −1=3−1=2 ⇒ { ((d_1 =((ac)/(c+2a.cos(B/3)))(4cos^2 (B/3)−1)=(((√(2.))(√2))/( (√2)+2(√2).((√3)/2))).2=(√6)−(√2))),((d_1 =((2ac)/(c+a(√3))),d_2 =((2ac)/(a+c(√3))))) :} ⇒d_1 =d_2 =(√6)−(√2) AD^2 =AB^2 +d_1 ^2 −2AB.d_1 .cos(B/3)⇒ AD^2 =c^2 +((4a^2 c^2 )/((c+a(√3))^2 ))−2c((2ac)/(c+a(√3))).((√3)/2)= =(c^2 /((c+a(√3))^2 ))(c^2 +3a^2 +2ac(√3)+4a^2 −6a^2 −2ac(√3))= =((c^2 (c^2 +a^2 ))/((c+a(√3))^2 ))=((c^2 b^2 )/((c+a(√3))^2 ))⇒ ⇒ { ((AD=((bc)/(c+a(√3)))=(2/(1+(√3)))=(√3)−1)),((CE=((ba)/(a+c(√3)))=AD=(√3)−1.)) :} DE=b−((bc)/(c+a(√3)))−((ba)/(a+c(√3)))= =(b/((c+a(√3))(a+c(√3))))(ac+c^2 (√3)+a^2 (√3)+3ac−ac−c^2 (√3)−ac−a^2 (√3))= ⇒DE=((2abc)/(4ac+b^2 (√3)))=((2.(√2).2.(√2))/(4(√2).(√2)+4(√3)))=(8/(4(2+(√3))))=2(2−(√3))=((√3)−1)^2 ⇒or:DE=AC−(AD+CE)=2−2((√3)−1)= =4−2(√3)=((√3)−1)^2 DH=HE=((DE)/( (√2)))=((((√3)−1)^2 )/( (√2))) ⇒S_(DHE) =(1/2)DH.HE=(1/2).((((√3)−1)^2 )/( (√2))).((((√3)−1)^2 )/( (√2)))= =(1/4)(4−2(√3))^2 =(2−(√3))^2 .■
$${if}\:\measuredangle{B}=\mathrm{90},{a}={c},{from}\:{the}\:{commonet}\: \\ $$$${above}\:,{we}\:{have}:\:\:\:\:\left(\frac{{B}}{\mathrm{3}}=\mathrm{30}°\right) \\ $$$${S}_{{ABC}} =\frac{\mathrm{1}}{\mathrm{2}}{ac}=\mathrm{1}\Rightarrow{ac}=\mathrm{2}\Rightarrow{a}={c}=\sqrt{\mathrm{2}},{b}=\mathrm{2} \\ $$$$\mathrm{4}\boldsymbol{{cos}}^{\mathrm{2}} \frac{\boldsymbol{{B}}}{\mathrm{3}}−\mathrm{1}=\mathrm{4}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} −\mathrm{1}=\mathrm{3}−\mathrm{1}=\mathrm{2} \\ $$$$\Rightarrow\begin{cases}{{d}_{\mathrm{1}} =\frac{{ac}}{{c}+\mathrm{2}{a}.{cos}\frac{{B}}{\mathrm{3}}}\left(\mathrm{4}{cos}^{\mathrm{2}} \frac{{B}}{\mathrm{3}}−\mathrm{1}\right)=\frac{\sqrt{\mathrm{2}.}\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{2}}+\mathrm{2}\sqrt{\mathrm{2}}.\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}.\mathrm{2}=\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}}}\\{{d}_{\mathrm{1}} =\frac{\mathrm{2}\boldsymbol{{ac}}}{\boldsymbol{{c}}+\boldsymbol{{a}}\sqrt{\mathrm{3}}},{d}_{\mathrm{2}} =\frac{\mathrm{2}\boldsymbol{{ac}}}{\boldsymbol{{a}}+\boldsymbol{{c}}\sqrt{\mathrm{3}}}}\end{cases} \\ $$$$\Rightarrow{d}_{\mathrm{1}} ={d}_{\mathrm{2}} =\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}} \\ $$$${AD}^{\mathrm{2}} ={AB}^{\mathrm{2}} +{d}_{\mathrm{1}} ^{\mathrm{2}} −\mathrm{2}{AB}.{d}_{\mathrm{1}} .{cos}\frac{{B}}{\mathrm{3}}\Rightarrow \\ $$$${AD}^{\mathrm{2}} ={c}^{\mathrm{2}} +\frac{\mathrm{4}{a}^{\mathrm{2}} {c}^{\mathrm{2}} }{\left({c}+\boldsymbol{{a}}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} }−\mathrm{2}\boldsymbol{{c}}\frac{\mathrm{2}\boldsymbol{{ac}}}{\boldsymbol{{c}}+\boldsymbol{{a}}\sqrt{\mathrm{3}}}.\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}= \\ $$$$=\frac{\boldsymbol{{c}}^{\mathrm{2}} }{\left(\boldsymbol{{c}}+\boldsymbol{{a}}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} }\left(\boldsymbol{{c}}^{\mathrm{2}} +\mathrm{3}\boldsymbol{{a}}^{\mathrm{2}} +\mathrm{2}\boldsymbol{{ac}}\sqrt{\mathrm{3}}+\mathrm{4}\boldsymbol{{a}}^{\mathrm{2}} −\mathrm{6}\boldsymbol{{a}}^{\mathrm{2}} −\mathrm{2}\boldsymbol{{ac}}\sqrt{\mathrm{3}}\right)= \\ $$$$=\frac{\boldsymbol{{c}}^{\mathrm{2}} \left(\boldsymbol{{c}}^{\mathrm{2}} +\boldsymbol{{a}}^{\mathrm{2}} \right)}{\left(\boldsymbol{{c}}+\boldsymbol{{a}}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} }=\frac{\boldsymbol{{c}}^{\mathrm{2}} \boldsymbol{{b}}^{\mathrm{2}} }{\left(\boldsymbol{{c}}+\boldsymbol{{a}}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} }\Rightarrow \\ $$$$\Rightarrow\begin{cases}{\boldsymbol{{AD}}=\frac{\boldsymbol{{bc}}}{\boldsymbol{{c}}+\boldsymbol{{a}}\sqrt{\mathrm{3}}}=\frac{\mathrm{2}}{\mathrm{1}+\sqrt{\mathrm{3}}}=\sqrt{\mathrm{3}}−\mathrm{1}}\\{\boldsymbol{{CE}}=\frac{\boldsymbol{{ba}}}{\boldsymbol{{a}}+\boldsymbol{{c}}\sqrt{\mathrm{3}}}=\boldsymbol{{AD}}=\sqrt{\mathrm{3}}−\mathrm{1}.}\end{cases} \\ $$$${DE}={b}−\frac{{bc}}{{c}+{a}\sqrt{\mathrm{3}}}−\frac{{ba}}{\boldsymbol{{a}}+\boldsymbol{{c}}\sqrt{\mathrm{3}}}= \\ $$$$=\frac{{b}}{\left({c}+{a}\sqrt{\mathrm{3}}\right)\left({a}+{c}\sqrt{\mathrm{3}}\right)}\left(\boldsymbol{{ac}}+\boldsymbol{{c}}^{\mathrm{2}} \sqrt{\mathrm{3}}+\boldsymbol{{a}}^{\mathrm{2}} \sqrt{\mathrm{3}}+\mathrm{3}\boldsymbol{{ac}}−\boldsymbol{{ac}}−\boldsymbol{{c}}^{\mathrm{2}} \sqrt{\mathrm{3}}−\boldsymbol{{ac}}−\boldsymbol{{a}}^{\mathrm{2}} \sqrt{\mathrm{3}}\right)= \\ $$$$\Rightarrow\boldsymbol{{DE}}=\frac{\mathrm{2}\boldsymbol{{abc}}}{\mathrm{4}\boldsymbol{{ac}}+\boldsymbol{{b}}^{\mathrm{2}} \sqrt{\mathrm{3}}}=\frac{\mathrm{2}.\sqrt{\mathrm{2}}.\mathrm{2}.\sqrt{\mathrm{2}}}{\mathrm{4}\sqrt{\mathrm{2}}.\sqrt{\mathrm{2}}+\mathrm{4}\sqrt{\mathrm{3}}}=\frac{\mathrm{8}}{\mathrm{4}\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)}=\mathrm{2}\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)=\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{or}:\boldsymbol{{DE}}={AC}−\left({AD}+{CE}\right)=\mathrm{2}−\mathrm{2}\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)= \\ $$$$=\mathrm{4}−\mathrm{2}\sqrt{\mathrm{3}}=\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$${DH}={HE}=\frac{{DE}}{\:\sqrt{\mathrm{2}}}=\frac{\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)^{\mathrm{2}} }{\:\sqrt{\mathrm{2}}} \\ $$$$\Rightarrow\boldsymbol{{S}}_{\boldsymbol{{DHE}}} =\frac{\mathrm{1}}{\mathrm{2}}{DH}.{HE}=\frac{\mathrm{1}}{\mathrm{2}}.\frac{\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)^{\mathrm{2}} }{\:\sqrt{\mathrm{2}}}.\frac{\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)^{\mathrm{2}} }{\:\sqrt{\mathrm{2}}}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{4}−\mathrm{2}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} =\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \:\:.\blacksquare \\ $$
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 25/May/17
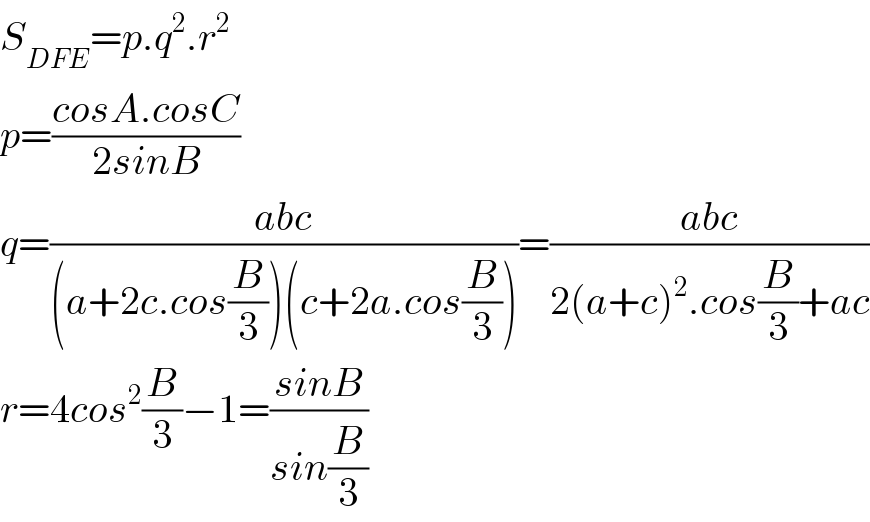
S_(DFE) =p.q^2 .r^2 p=((cosA.cosC)/(2sinB)) q=((abc)/((a+2c.cos(B/3))(c+2a.cos(B/3))))=((abc)/(2(a+c)^2 .cos(B/3)+ac)) r=4cos^2 (B/3)−1=((sinB)/(sin(B/3)))
$${S}_{{DFE}} ={p}.{q}^{\mathrm{2}} .{r}^{\mathrm{2}} \\ $$$${p}=\frac{{cosA}.{cosC}}{\mathrm{2}{sinB}} \\ $$$${q}=\frac{{abc}}{\left({a}+\mathrm{2}{c}.{cos}\frac{{B}}{\mathrm{3}}\right)\left({c}+\mathrm{2}{a}.{cos}\frac{{B}}{\mathrm{3}}\right)}=\frac{{abc}}{\mathrm{2}\left({a}+{c}\right)^{\mathrm{2}} .{cos}\frac{{B}}{\mathrm{3}}+{ac}} \\ $$$${r}=\mathrm{4}{cos}^{\mathrm{2}} \frac{{B}}{\mathrm{3}}−\mathrm{1}=\frac{{sinB}}{{sin}\frac{{B}}{\mathrm{3}}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *