Question Number 13687 by christine last updated on 22/May/17
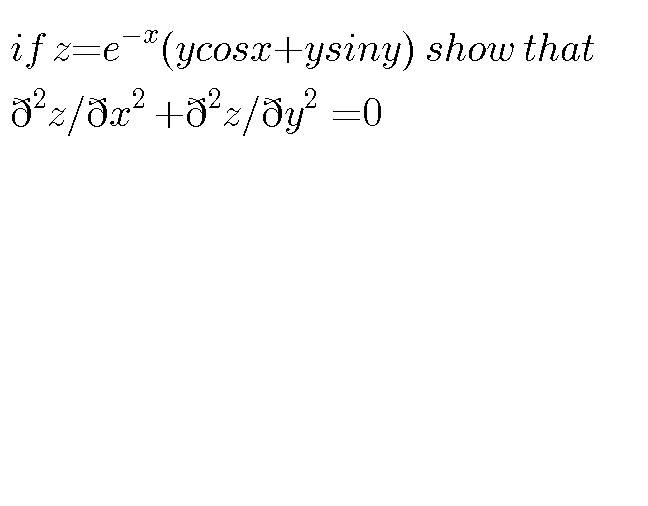
Commented by mrW1 last updated on 22/May/17

$${The}\:{question}\:{is}\:{wrong}.\:{It}\:{should}\:{be} \\ $$$$\boldsymbol{{z}}=\boldsymbol{{e}}^{−\boldsymbol{{x}}} \left(\boldsymbol{{y}}\mathrm{cos}\:\boldsymbol{{x}}+\boldsymbol{{x}}\mathrm{sin}\:\boldsymbol{{y}}\right) \\ $$$$ \\ $$$${see}\:{Q}\mathrm{13544}. \\ $$
Commented by aishadenge last updated on 22/May/17
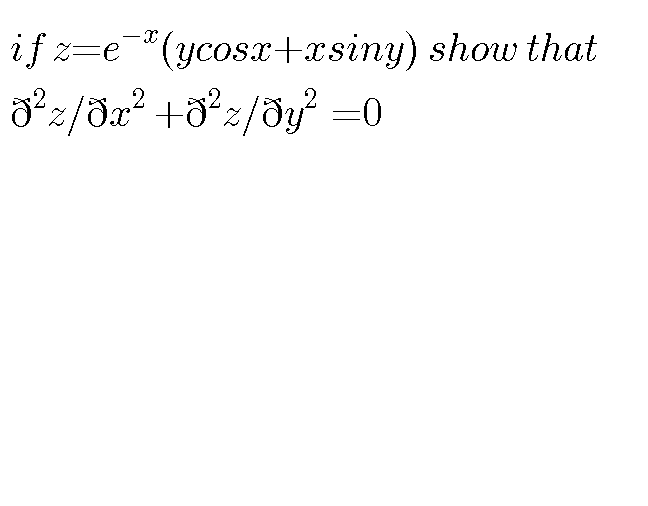
Commented by ajfour last updated on 22/May/17
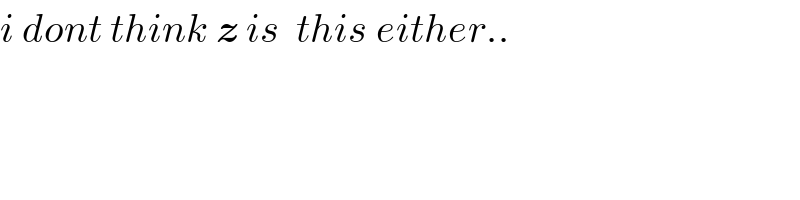
$${i}\:{dont}\:{think}\:\boldsymbol{{z}}\:{is}\:\:{this}\:{either}.. \\ $$
Commented by prakash jain last updated on 22/May/17

$${z}={e}^{−{x}} \left({y}\mathrm{cos}\:{x}+{x}\mathrm{sin}\:{y}\right) \\ $$$$\frac{\partial{z}}{\partial{x}}={e}^{−{x}} \left(−{y}\mathrm{sin}\:{x}+\mathrm{sin}\:{y}\right)−{e}^{−{x}} \left({y}\mathrm{cos}\:{x}+{x}\mathrm{sin}\:{y}\right) \\ $$$$={e}^{−{x}} \left(−{x}\mathrm{sin}\:{y}+\mathrm{sin}\:{y}+{y}\mathrm{cos}\:{x}−{y}\mathrm{sin}\:{x}\right) \\ $$$$\frac{\partial^{\mathrm{2}} {z}}{\partial{x}^{\mathrm{2}} }={e}^{−{x}} \left(−\mathrm{sin}\:{y}−\mathrm{sin}\:{x}−\mathrm{cos}\:{x}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:−{e}^{−{x}} \left(−{x}\mathrm{sin}\:{y}+\mathrm{sin}\:{y}+{y}\mathrm{cos}\:{x}−{y}\mathrm{sin}\:{x}\right) \\ $$$$={e}^{−{x}} \left(\mathrm{sin}\:{y}−\mathrm{sin}\:{x}−\mathrm{cos}\:{x}+{x}\mathrm{sin}\:{y}−\mathrm{sin}\:{y}+{y}\mathrm{sin}\:{x}−{y}\mathrm{cos}\:{x}\right) \\ $$$$={e}^{−{x}} \left(−\mathrm{sin}\:{x}−\mathrm{cos}\:{x}+{x}\mathrm{sin}\:{y}+{y}\mathrm{sin}\:{x}−{y}\mathrm{cos}\:{x}\right) \\ $$$$\frac{\partial{z}}{\partial{y}}={e}^{−{x}} \left(\mathrm{cos}\:{x}+{x}\mathrm{cos}\:{y}\right) \\ $$$$\frac{\partial^{\mathrm{2}} {z}}{\partial{y}^{\mathrm{2}} }=−{xe}^{−{x}} \mathrm{sin}\:{y} \\ $$$$\mathrm{I}\:\mathrm{think}\:\mathrm{question}\:\mathrm{is}\:\mathrm{not}\:\mathrm{correct}. \\ $$
