Menu Close

Question-13735

Tinku Tara 0 Comments
Pin




Question Number 13735 by b.e.h.i.8.3.4.1.7@gmail.com last updated on 22/May/17
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 22/May/17
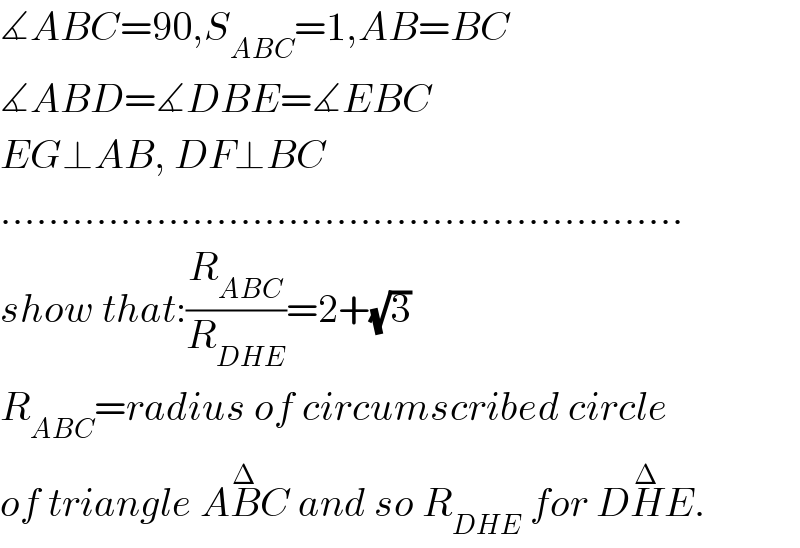
∡ABC=90,S_(ABC) =1,AB=BC ∡ABD=∡DBE=∡EBC EG⊥AB, DF⊥BC ......................................................... show that:(R_(ABC) /R_(DHE) )=2+(√3) R_(ABC) =radius of circumscribed circle of triangle AB^Δ C and so R_(DHE) for DH^Δ E.
$$\measuredangle{ABC}=\mathrm{90},{S}_{{ABC}} =\mathrm{1},{AB}={BC} \\ $$$$\measuredangle{ABD}=\measuredangle{DBE}=\measuredangle{EBC} \\ $$$${EG}\bot{AB},\:{DF}\bot{BC} \\ $$$$………………………………………………… \\ $$$${show}\:{that}:\frac{{R}_{{ABC}} }{{R}_{{DHE}} }=\mathrm{2}+\sqrt{\mathrm{3}} \\ $$$${R}_{{ABC}} ={radius}\:{of}\:{circumscribed}\:{circle} \\ $$$${of}\:{triangle}\:{A}\overset{\Delta} {{B}C}\:{and}\:{so}\:{R}_{{DHE}} \:{for}\:{D}\overset{\Delta} {{H}E}. \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 23/May/17
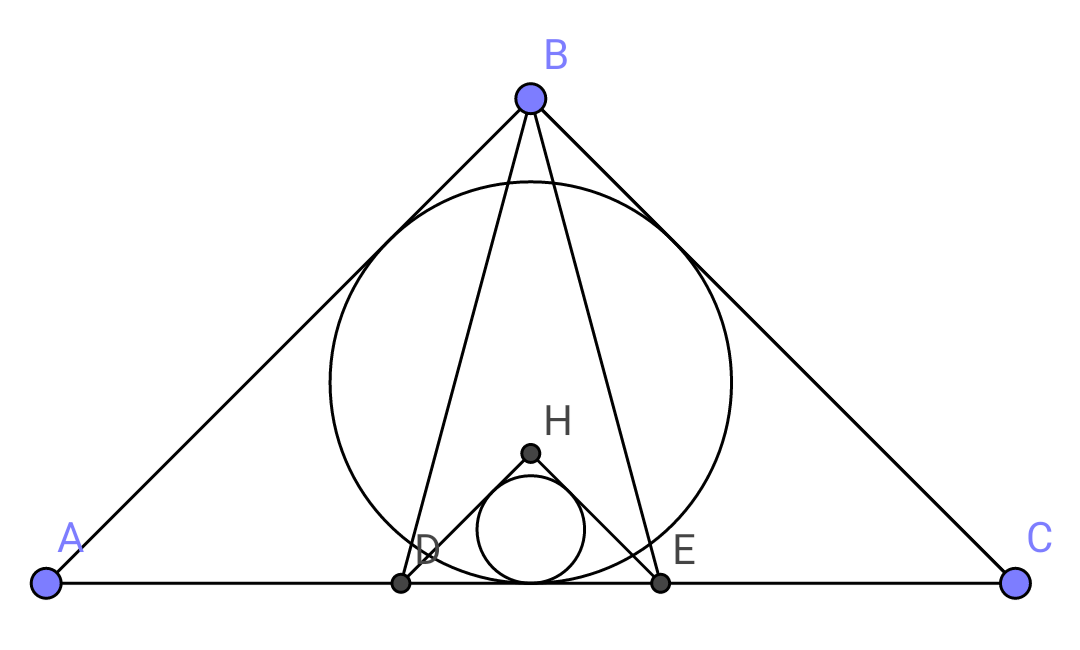
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 23/May/17
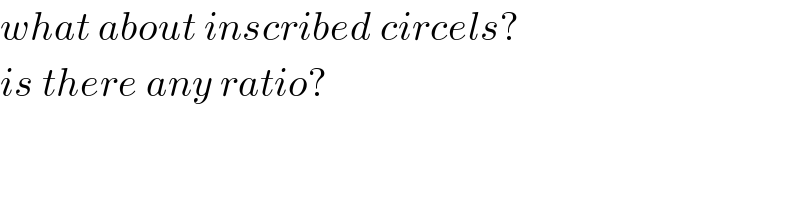
what about inscribed circels? is there any ratio?
$${what}\:{about}\:{inscribed}\:{circels}? \\ $$$${is}\:{there}\:{any}\:{ratio}? \\ $$
Commented by ajfour last updated on 23/May/17
Commented by ajfour last updated on 23/May/17
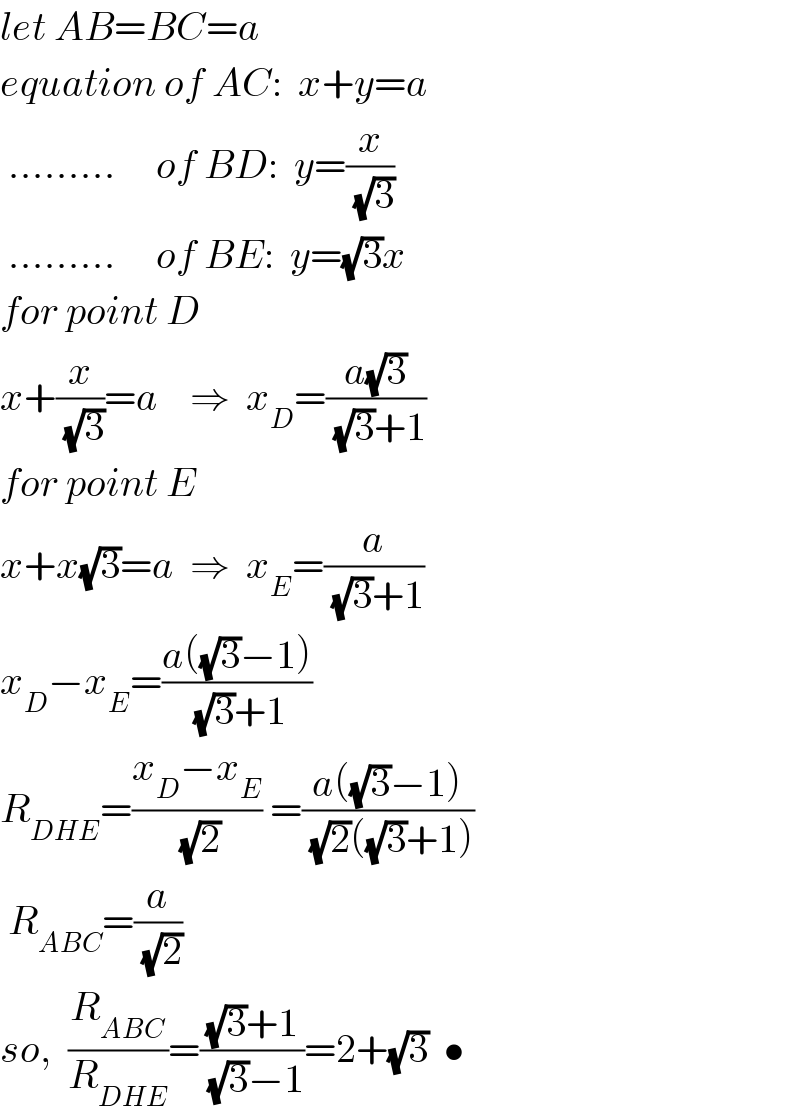
let AB=BC=a equation of AC: x+y=a ......... of BD: y=(x/( (√3))) ......... of BE: y=(√3)x for point D x+(x/( (√3)))=a ⇒ x_D =((a(√3))/( (√3)+1)) for point E x+x(√3)=a ⇒ x_E =(a/( (√3)+1)) x_D −x_E =((a((√3)−1))/( (√3)+1)) R_(DHE) =((x_D −x_E )/( (√2))) =((a((√3)−1))/( (√2)((√3)+1))) R_(ABC) =(a/( (√2))) so, (R_(ABC) /R_(DHE) )=(((√3)+1)/( (√3)−1))=2+(√3) •
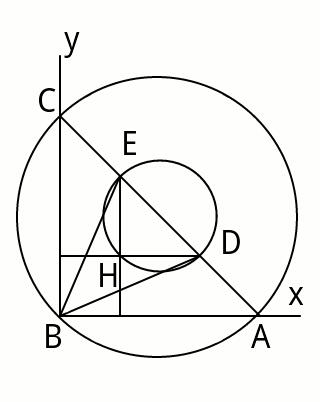
$${let}\:{AB}={BC}={a} \\ $$$${equation}\:{of}\:{AC}:\:\:{x}+{y}={a} \\ $$$$\:………\:\:\:\:\:{of}\:{BD}:\:\:{y}=\frac{{x}}{\:\sqrt{\mathrm{3}}} \\ $$$$\:………\:\:\:\:\:{of}\:{BE}:\:\:{y}=\sqrt{\mathrm{3}}{x} \\ $$$${for}\:{point}\:{D} \\ $$$${x}+\frac{{x}}{\:\sqrt{\mathrm{3}}}={a}\:\:\:\:\Rightarrow\:\:{x}_{{D}} =\frac{{a}\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{3}}+\mathrm{1}} \\ $$$${for}\:{point}\:{E} \\ $$$${x}+{x}\sqrt{\mathrm{3}}={a}\:\:\Rightarrow\:\:{x}_{{E}} =\frac{{a}}{\:\sqrt{\mathrm{3}}+\mathrm{1}} \\ $$$${x}_{{D}} −{x}_{{E}} =\frac{{a}\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)}{\:\sqrt{\mathrm{3}}+\mathrm{1}} \\ $$$${R}_{{DHE}} =\frac{{x}_{{D}} −{x}_{{E}} }{\:\sqrt{\mathrm{2}}}\:=\frac{{a}\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)}{\:\sqrt{\mathrm{2}}\left(\sqrt{\mathrm{3}}+\mathrm{1}\right)} \\ $$$$\:{R}_{{ABC}} =\frac{{a}}{\:\sqrt{\mathrm{2}}} \\ $$$${so},\:\:\frac{{R}_{{ABC}} }{{R}_{{DHE}} }=\frac{\sqrt{\mathrm{3}}+\mathrm{1}}{\:\sqrt{\mathrm{3}}−\mathrm{1}}=\mathrm{2}+\sqrt{\mathrm{3}}\:\:\bullet \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 25/May/17
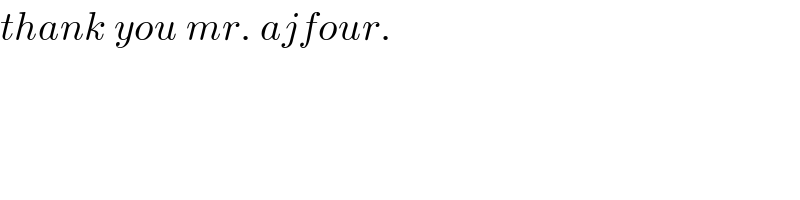
thank you mr. ajfour.
$${thank}\:{you}\:{mr}.\:{ajfour}. \\ $$
Answered by mrW1 last updated on 22/May/17
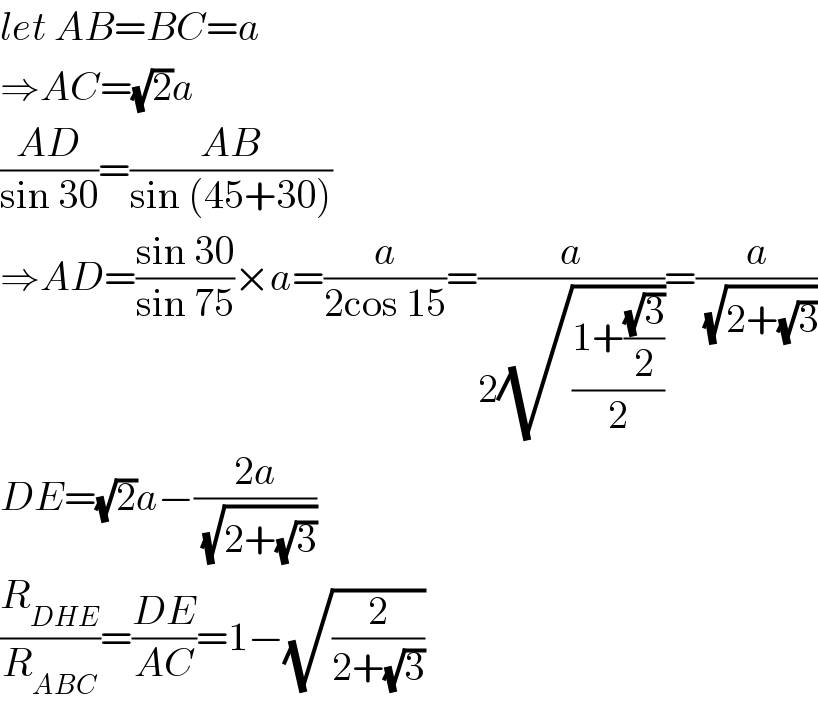
let AB=BC=a ⇒AC=(√2)a ((AD)/(sin 30))=((AB)/(sin (45+30))) ⇒AD=((sin 30)/(sin 75))×a=(a/(2cos 15))=(a/(2(√((1+((√3)/2))/2))))=(a/( (√(2+(√3))))) DE=(√2)a−((2a)/( (√(2+(√3))))) (R_(DHE) /R_(ABC) )=((DE)/(AC))=1−(√(2/(2+(√3))))
$${let}\:{AB}={BC}={a} \\ $$$$\Rightarrow{AC}=\sqrt{\mathrm{2}}{a} \\ $$$$\frac{{AD}}{\mathrm{sin}\:\mathrm{30}}=\frac{{AB}}{\mathrm{sin}\:\left(\mathrm{45}+\mathrm{30}\right)} \\ $$$$\Rightarrow{AD}=\frac{\mathrm{sin}\:\mathrm{30}}{\mathrm{sin}\:\mathrm{75}}×{a}=\frac{{a}}{\mathrm{2cos}\:\mathrm{15}}=\frac{{a}}{\mathrm{2}\sqrt{\frac{\mathrm{1}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}{\mathrm{2}}}}=\frac{{a}}{\:\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}} \\ $$$${DE}=\sqrt{\mathrm{2}}{a}−\frac{\mathrm{2}{a}}{\:\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}} \\ $$$$\frac{{R}_{{DHE}} }{{R}_{{ABC}} }=\frac{{DE}}{{AC}}=\mathrm{1}−\sqrt{\frac{\mathrm{2}}{\mathrm{2}+\sqrt{\mathrm{3}}}} \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 23/May/17
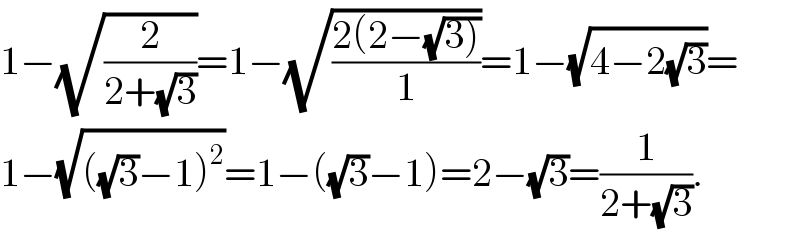
1−(√(2/(2+(√3))))=1−(√((2(2−(√(3))))/1))=1−(√(4−2(√3)))= 1−(√(((√3)−1)^2 ))=1−((√3)−1)=2−(√3)=(1/(2+(√3))).
$$\mathrm{1}−\sqrt{\frac{\mathrm{2}}{\mathrm{2}+\sqrt{\mathrm{3}}}}=\mathrm{1}−\sqrt{\frac{\mathrm{2}\left(\mathrm{2}−\sqrt{\left.\mathrm{3}\right)}\right.}{\mathrm{1}}}=\mathrm{1}−\sqrt{\mathrm{4}−\mathrm{2}\sqrt{\mathrm{3}}}= \\ $$$$\mathrm{1}−\sqrt{\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)^{\mathrm{2}} }=\mathrm{1}−\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)=\mathrm{2}−\sqrt{\mathrm{3}}=\frac{\mathrm{1}}{\mathrm{2}+\sqrt{\mathrm{3}}}. \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 25/May/17
thank you mrW1.
$${thank}\:{you}\:{mrW}\mathrm{1}. \\ $$
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 23/May/17
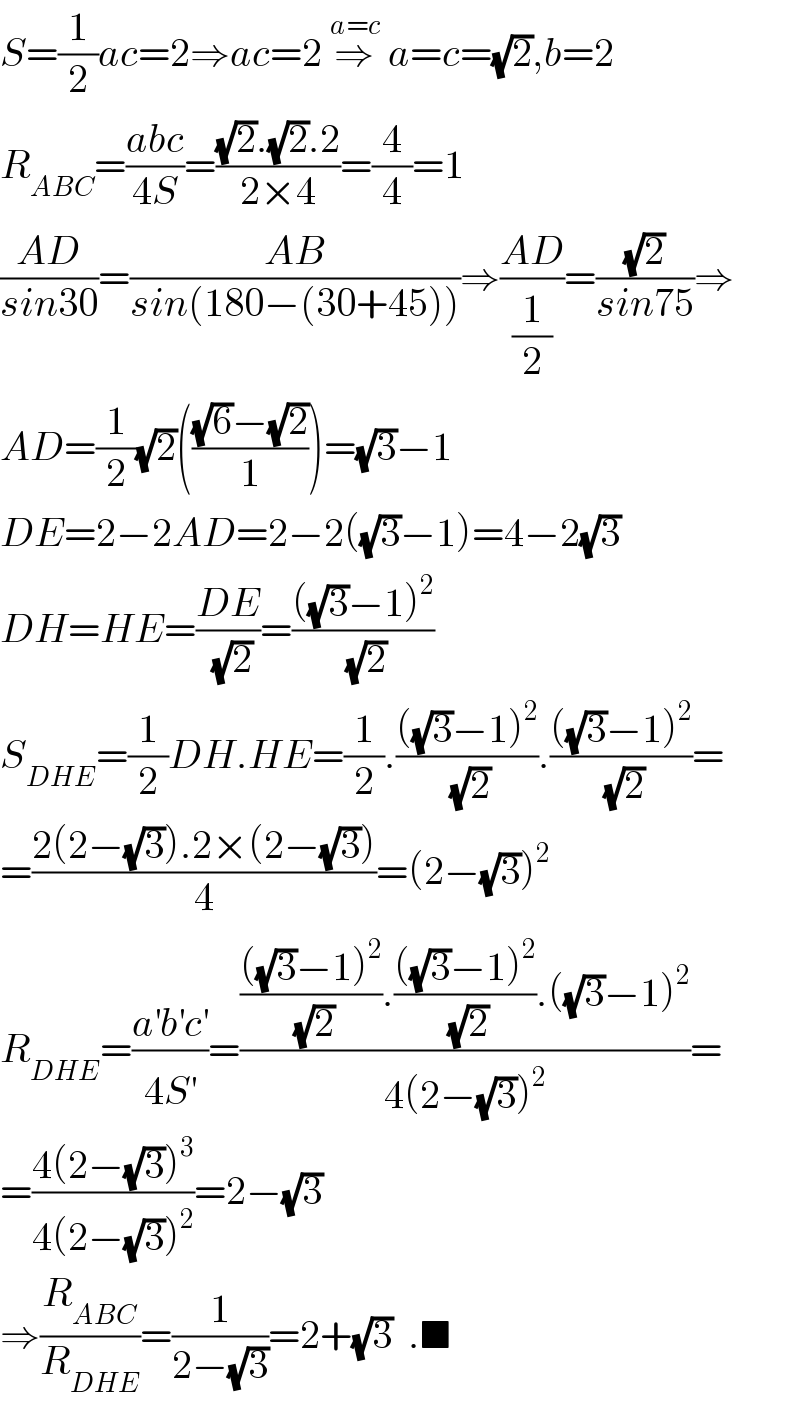
S=(1/2)ac=2⇒ac=2 ⇒^(a=c) a=c=(√2),b=2 R_(ABC) =((abc)/(4S))=(((√2).(√2).2)/(2×4))=(4/4)=1 ((AD)/(sin30))=((AB)/(sin(180−(30+45))))⇒((AD)/(1/2))=((√2)/(sin75))⇒ AD=(1/2)(√2)((((√6)−(√2))/1))=(√3)−1 DE=2−2AD=2−2((√3)−1)=4−2(√3) DH=HE=((DE)/( (√2)))=((((√3)−1)^2 )/( (√2))) S_(DHE) =(1/2)DH.HE=(1/2).((((√3)−1)^2 )/( (√2))).((((√3)−1)^2 )/( (√2)))= =((2(2−(√3)).2×(2−(√3)))/4)=(2−(√3))^2 R_(DHE) =((a^′ b^′ c^′ )/(4S^′ ))=((((((√3)−1)^2 )/( (√2))).((((√3)−1)^2 )/( (√2))).((√3)−1)^2 )/(4(2−(√3))^2 ))= =((4(2−(√3))^3 )/(4(2−(√3))^2 ))=2−(√3) ⇒(R_(ABC) /R_(DHE) )=(1/(2−(√3)))=2+(√3) .■
$${S}=\frac{\mathrm{1}}{\mathrm{2}}{ac}=\mathrm{2}\Rightarrow{ac}=\mathrm{2}\:\overset{{a}={c}} {\Rightarrow}\:{a}={c}=\sqrt{\mathrm{2}},{b}=\mathrm{2} \\ $$$${R}_{{ABC}} =\frac{{abc}}{\mathrm{4}{S}}=\frac{\sqrt{\mathrm{2}}.\sqrt{\mathrm{2}}.\mathrm{2}}{\mathrm{2}×\mathrm{4}}=\frac{\mathrm{4}}{\mathrm{4}}=\mathrm{1} \\ $$$$\frac{{AD}}{{sin}\mathrm{30}}=\frac{{AB}}{{sin}\left(\mathrm{180}−\left(\mathrm{30}+\mathrm{45}\right)\right)}\Rightarrow\frac{{AD}}{\frac{\mathrm{1}}{\mathrm{2}}}=\frac{\sqrt{\mathrm{2}}}{{sin}\mathrm{75}}\Rightarrow \\ $$$${AD}=\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{2}}\left(\frac{\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}}}{\mathrm{1}}\right)=\sqrt{\mathrm{3}}−\mathrm{1} \\ $$$${DE}=\mathrm{2}−\mathrm{2}{AD}=\mathrm{2}−\mathrm{2}\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)=\mathrm{4}−\mathrm{2}\sqrt{\mathrm{3}} \\ $$$${DH}={HE}=\frac{{DE}}{\:\sqrt{\mathrm{2}}}=\frac{\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)^{\mathrm{2}} }{\:\sqrt{\mathrm{2}}} \\ $$$${S}_{{DHE}} =\frac{\mathrm{1}}{\mathrm{2}}{DH}.{HE}=\frac{\mathrm{1}}{\mathrm{2}}.\frac{\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)^{\mathrm{2}} }{\:\sqrt{\mathrm{2}}}.\frac{\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)^{\mathrm{2}} }{\:\sqrt{\mathrm{2}}}= \\ $$$$=\frac{\mathrm{2}\left(\mathrm{2}−\sqrt{\mathrm{3}}\right).\mathrm{2}×\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)}{\mathrm{4}}=\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \\ $$$${R}_{{DHE}} =\frac{{a}^{'} {b}^{'} {c}^{'} }{\mathrm{4}{S}^{'} }=\frac{\frac{\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)^{\mathrm{2}} }{\:\sqrt{\mathrm{2}}}.\frac{\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)^{\mathrm{2}} }{\:\sqrt{\mathrm{2}}}.\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{4}\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)^{\mathrm{2}} }= \\ $$$$=\frac{\mathrm{4}\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)^{\mathrm{3}} }{\mathrm{4}\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)^{\mathrm{2}} }=\mathrm{2}−\sqrt{\mathrm{3}} \\ $$$$\Rightarrow\frac{{R}_{{ABC}} }{{R}_{{DHE}} }=\frac{\mathrm{1}}{\mathrm{2}−\sqrt{\mathrm{3}}}=\mathrm{2}+\sqrt{\mathrm{3}}\:\:.\blacksquare \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *