Question Number 13832 by tawa tawa last updated on 24/May/17

Answered by ajfour last updated on 24/May/17

Commented by ajfour last updated on 24/May/17
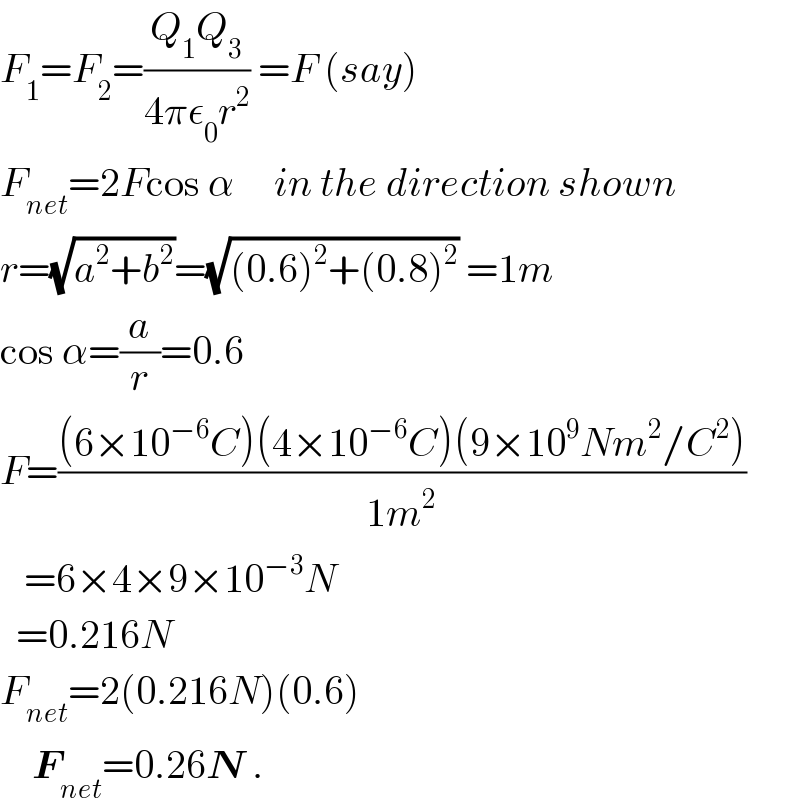
$${F}_{\mathrm{1}} ={F}_{\mathrm{2}} =\frac{{Q}_{\mathrm{1}} {Q}_{\mathrm{3}} }{\mathrm{4}\pi\epsilon_{\mathrm{0}} {r}^{\mathrm{2}} }\:={F}\:\left({say}\right) \\ $$$${F}_{{net}} =\mathrm{2}{F}\mathrm{cos}\:\alpha\:\:\:\:\:{in}\:{the}\:{direction}\:{shown} \\ $$$${r}=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }=\sqrt{\left(\mathrm{0}.\mathrm{6}\right)^{\mathrm{2}} +\left(\mathrm{0}.\mathrm{8}\right)^{\mathrm{2}} }\:=\mathrm{1}{m} \\ $$$$\mathrm{cos}\:\alpha=\frac{{a}}{{r}}=\mathrm{0}.\mathrm{6} \\ $$$${F}=\frac{\left(\mathrm{6}×\mathrm{10}^{−\mathrm{6}} {C}\right)\left(\mathrm{4}×\mathrm{10}^{−\mathrm{6}} {C}\right)\left(\mathrm{9}×\mathrm{10}^{\mathrm{9}} {Nm}^{\mathrm{2}} /{C}^{\mathrm{2}} \right)}{\mathrm{1}{m}^{\mathrm{2}} } \\ $$$$\:\:\:=\mathrm{6}×\mathrm{4}×\mathrm{9}×\mathrm{10}^{−\mathrm{3}} {N} \\ $$$$\:\:=\mathrm{0}.\mathrm{216}{N} \\ $$$${F}_{{net}} =\mathrm{2}\left(\mathrm{0}.\mathrm{216}{N}\right)\left(\mathrm{0}.\mathrm{6}\right) \\ $$$$\:\:\:\:\boldsymbol{{F}}_{{net}} =\mathrm{0}.\mathrm{26}\boldsymbol{{N}}\:. \\ $$
Commented by tawa tawa last updated on 24/May/17
$$\mathrm{Wow},\:\mathrm{Am}\:\mathrm{really}\:\mathrm{greatful}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
