Question Number 13886 by tawa tawa last updated on 24/May/17

Answered by ajfour last updated on 24/May/17
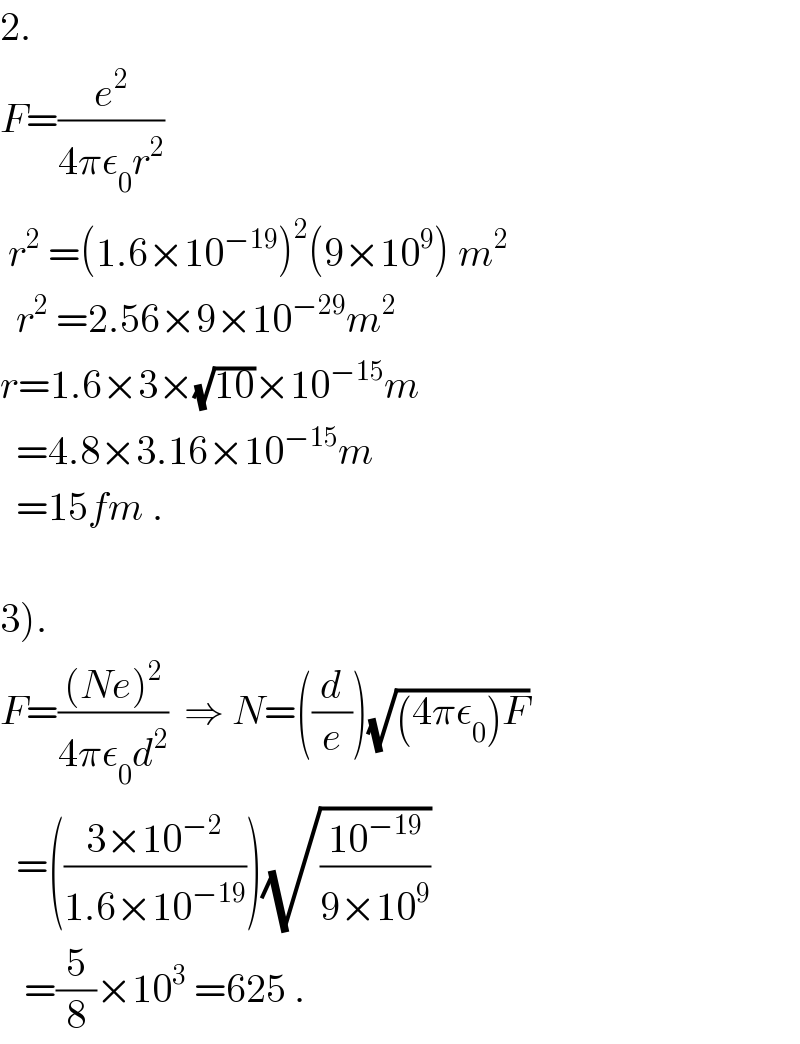
$$\mathrm{2}. \\ $$$${F}=\frac{{e}^{\mathrm{2}} }{\mathrm{4}\pi\epsilon_{\mathrm{0}} {r}^{\mathrm{2}} } \\ $$$$\:{r}^{\mathrm{2}} \:=\left(\mathrm{1}.\mathrm{6}×\mathrm{10}^{−\mathrm{19}} \right)^{\mathrm{2}} \left(\mathrm{9}×\mathrm{10}^{\mathrm{9}} \right)\:{m}^{\mathrm{2}} \\ $$$$\:\:{r}^{\mathrm{2}} \:=\mathrm{2}.\mathrm{56}×\mathrm{9}×\mathrm{10}^{−\mathrm{29}} {m}^{\mathrm{2}} \\ $$$${r}=\mathrm{1}.\mathrm{6}×\mathrm{3}×\sqrt{\mathrm{10}}×\mathrm{10}^{−\mathrm{15}} {m} \\ $$$$\:\:=\mathrm{4}.\mathrm{8}×\mathrm{3}.\mathrm{16}×\mathrm{10}^{−\mathrm{15}} {m} \\ $$$$\:\:=\mathrm{15}{fm}\:. \\ $$$$ \\ $$$$\left.\mathrm{3}\right). \\ $$$${F}=\frac{\left({Ne}\right)^{\mathrm{2}} }{\mathrm{4}\pi\epsilon_{\mathrm{0}} {d}^{\mathrm{2}} }\:\:\Rightarrow\:{N}=\left(\frac{{d}}{{e}}\right)\sqrt{\left(\mathrm{4}\pi\epsilon_{\mathrm{0}} \right){F}}\: \\ $$$$\:\:=\left(\frac{\mathrm{3}×\mathrm{10}^{−\mathrm{2}} }{\mathrm{1}.\mathrm{6}×\mathrm{10}^{−\mathrm{19}} }\right)\sqrt{\frac{\mathrm{10}^{−\mathrm{19}} }{\mathrm{9}×\mathrm{10}^{\mathrm{9}} }}\: \\ $$$$\:\:\:=\frac{\mathrm{5}}{\mathrm{8}}×\mathrm{10}^{\mathrm{3}} \:=\mathrm{625}\:. \\ $$
Commented by tawa tawa last updated on 24/May/17

$$\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{effort}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\: \\ $$
