Menu Close

Question-14157

Tinku Tara 0 Comments
Pin




Question Number 14157 by b.e.h.i.8.3.4.1.7@gmail.com last updated on 29/May/17
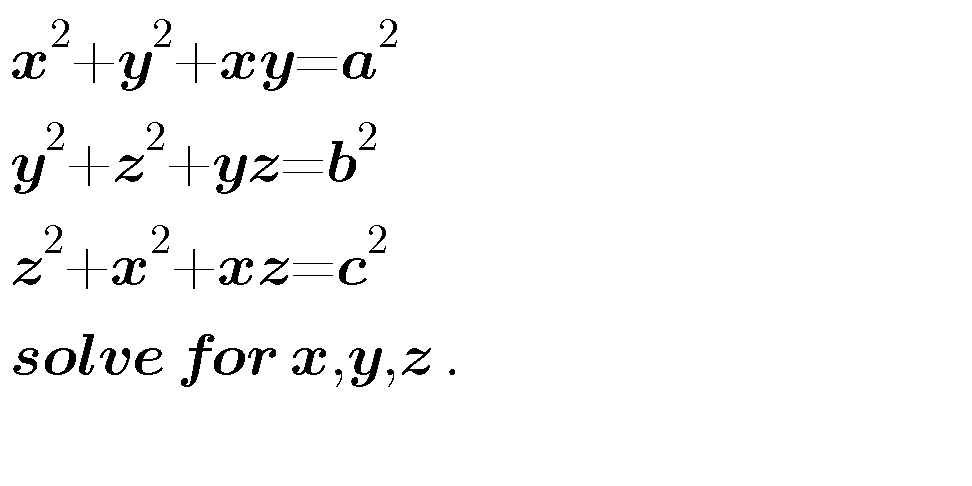
Commented by ajfour last updated on 30/May/17
kindly view my solution in Q.14306 solved by coordinate geometry..
$${kindly}\:{view}\:{my}\:{solution}\:{in} \\ $$$${Q}.\mathrm{14306}\:{solved}\:{by}\:{coordinate} \\ $$$${geometry}.. \\ $$
Commented by RasheedSindhi last updated on 31/May/17
x^2 +y^2 +xy=a^2 ⇒a^2 =x^2 +y^2 −2xy cos(((2π)/3)) y^2 +z^2 +yz=b^2 ⇒b^2 =y^2 +z^2 −2yz cos(((2π)/3)) z^2 +x^2 +zx=c^2 ⇒c^2 =z^2 +x^2 −2zx cos(((2π)/3)) Three triangles with one angle equal to 120° and some sides common... Many relations can be established from the above concept: α=cos^(-1) (((x^2 +a^2 −y^2 )/(2xa))) β=cos^(-1) (((x^2 +c^2 −z^2 )/(2xc))) α+β=cos^(-1) (((x^2 +a^2 −y^2 )/(2xa)))+cos^(-1) (((x^2 +c^2 −z^2 )/(2xc))) sum of above α+β=cos^(-1) (((a^2 +c^2 −b^2 )/(2ac))) from △(a,b,c) By comparison cos^(-1) (((x^2 +a^2 −y^2 )/(2xa)))+cos^(-1) (((x^2 +c^2 −z^2 )/(2xc))) =cos^(-1) (((a^2 +c^2 −b^2 )/(2ac))) cos(α+β)=cosα cosβ−sinα sinβ cos{cos^(-1) (((a^2 +c^2 −b^2 )/(2ac)))} =cos(cos^(-1) (((x^2 +a^2 −y^2 )/(2xa))))cos(cos^(-1) (((x^2 +c^2 −z^2 )/(2xc)))) −sin(cos^(-1) (((x^2 +a^2 −y^2 )/(2xa))))sin(cos^(-1) (((x^2 +c^2 −z^2 )/(2xc)))) ((a^2 +c^2 −b^2 )/(2ac)) =(((x^2 +a^2 −y^2 )/(2xa)))(((x^2 +c^2 −z^2 )/(2xc))) −sin(cos^(-1) (((x^2 +a^2 −y^2 )/(2xa))))sin(cos^(-1) (((x^2 +c^2 −z^2 )/(2xc)))) Pl help me in last line. Continue
$$\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} +\mathrm{xy}=\mathrm{a}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{a}^{\mathrm{2}} =\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} −\mathrm{2xy}\:\mathrm{cos}\left(\frac{\mathrm{2}\pi}{\mathrm{3}}\right) \\ $$$$\mathrm{y}^{\mathrm{2}} +\mathrm{z}^{\mathrm{2}} +\mathrm{yz}=\mathrm{b}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{b}^{\mathrm{2}} =\mathrm{y}^{\mathrm{2}} +\mathrm{z}^{\mathrm{2}} −\mathrm{2yz}\:\mathrm{cos}\left(\frac{\mathrm{2}\pi}{\mathrm{3}}\right)\: \\ $$$$\mathrm{z}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} +\mathrm{zx}=\mathrm{c}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{c}^{\mathrm{2}} =\mathrm{z}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} −\mathrm{2zx}\:\mathrm{cos}\left(\frac{\mathrm{2}\pi}{\mathrm{3}}\right)\: \\ $$$$\mathrm{Three}\:\mathrm{triangles}\:\mathrm{with}\:\mathrm{one}\:\mathrm{angle} \\ $$$$\mathrm{equal}\:\mathrm{to}\:\mathrm{120}°\:\mathrm{and}\:\mathrm{some}\:\mathrm{sides} \\ $$$$\mathrm{common}… \\ $$$$\mathrm{Many}\:\mathrm{relations}\:\mathrm{can}\:\mathrm{be}\:\mathrm{established} \\ $$$$\mathrm{from}\:\mathrm{the}\:\mathrm{above}\:\mathrm{concept}: \\ $$$$\:\:\:\alpha=\mathrm{cos}^{-\mathrm{1}} \left(\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} }{\mathrm{2xa}}\right) \\ $$$$\:\:\:\beta=\mathrm{cos}^{-\mathrm{1}} \left(\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} −\mathrm{z}^{\mathrm{2}} }{\mathrm{2xc}}\right) \\ $$$$\:\:\:\alpha+\beta=\mathrm{cos}^{-\mathrm{1}} \left(\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} }{\mathrm{2xa}}\right)+\mathrm{cos}^{-\mathrm{1}} \left(\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} −\mathrm{z}^{\mathrm{2}} }{\mathrm{2xc}}\right)\:\mathrm{sum}\:\mathrm{of}\:\mathrm{above} \\ $$$$\:\:\:\alpha+\beta=\mathrm{cos}^{-\mathrm{1}} \left(\frac{\mathrm{a}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} }{\mathrm{2ac}}\right)\:\mathrm{from}\:\bigtriangleup\left(\mathrm{a},\mathrm{b},\mathrm{c}\right) \\ $$$$\mathrm{By}\:\mathrm{comparison} \\ $$$$\mathrm{cos}^{-\mathrm{1}} \left(\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} }{\mathrm{2xa}}\right)+\mathrm{cos}^{-\mathrm{1}} \left(\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} −\mathrm{z}^{\mathrm{2}} }{\mathrm{2xc}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{cos}^{-\mathrm{1}} \left(\frac{\mathrm{a}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} }{\mathrm{2ac}}\right) \\ $$$$\mathrm{cos}\left(\alpha+\beta\right)=\mathrm{cos}\alpha\:\mathrm{cos}\beta−\mathrm{sin}\alpha\:\mathrm{sin}\beta\: \\ $$$$\mathrm{cos}\left\{\mathrm{cos}^{-\mathrm{1}} \left(\frac{\mathrm{a}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} }{\mathrm{2ac}}\right)\right\} \\ $$$$\:\:\:\:\:\:=\mathrm{cos}\left(\mathrm{cos}^{-\mathrm{1}} \left(\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} }{\mathrm{2xa}}\right)\right)\mathrm{cos}\left(\mathrm{cos}^{-\mathrm{1}} \left(\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} −\mathrm{z}^{\mathrm{2}} }{\mathrm{2xc}}\right)\right) \\ $$$$\:\:\:\:\:\:−\mathrm{sin}\left(\mathrm{cos}^{-\mathrm{1}} \left(\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} }{\mathrm{2xa}}\right)\right)\mathrm{sin}\left(\mathrm{cos}^{-\mathrm{1}} \left(\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} −\mathrm{z}^{\mathrm{2}} }{\mathrm{2xc}}\right)\right) \\ $$$$\frac{\mathrm{a}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} }{\mathrm{2ac}} \\ $$$$\:\:\:\:\:\:=\left(\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} }{\mathrm{2xa}}\right)\left(\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} −\mathrm{z}^{\mathrm{2}} }{\mathrm{2xc}}\right) \\ $$$$\:\:\:\:\:\:−\mathrm{sin}\left(\mathrm{cos}^{-\mathrm{1}} \left(\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} }{\mathrm{2xa}}\right)\right)\mathrm{sin}\left(\mathrm{cos}^{-\mathrm{1}} \left(\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} −\mathrm{z}^{\mathrm{2}} }{\mathrm{2xc}}\right)\right) \\ $$$$\:\:\:\mathrm{Pl}\:\mathrm{help}\:\mathrm{me}\:\mathrm{in}\:\mathrm{last}\:\mathrm{line}. \\ $$$$ \\ $$$$\mathrm{Continue} \\ $$
Commented by RasheedSindhi last updated on 30/May/17
Commented by mrW1 last updated on 30/May/17
This is great! It shows the condition when solution exists: if a^2 , b^2 and c^2 can form a triangle, there is a solution!
$${This}\:{is}\:{great}!\:{It}\:{shows}\:{the}\:{condition} \\ $$$${when}\:{solution}\:{exists}: \\ $$$${if}\:{a}^{\mathrm{2}} ,\:{b}^{\mathrm{2}} \:{and}\:{c}^{\mathrm{2}} \:{can}\:{form}\:{a}\:{triangle}, \\ $$$${there}\:{is}\:{a}\:{solution}! \\ $$
Commented by prakash jain last updated on 30/May/17
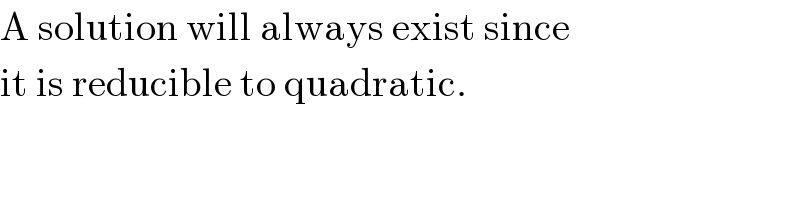
A solution will always exist since it is reducible to quadratic.
$$\mathrm{A}\:\mathrm{solution}\:\mathrm{will}\:\mathrm{always}\:\mathrm{exist}\:\mathrm{since} \\ $$$$\mathrm{it}\:\mathrm{is}\:\mathrm{reducible}\:\mathrm{to}\:\mathrm{quadratic}. \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 30/May/17
dear mrW1! way a^2 ,b^2 ,c^2 ?way not :a,b,c?
$${dear}\:{mrW}\mathrm{1}!\:{way}\:{a}^{\mathrm{2}} ,{b}^{\mathrm{2}} ,{c}^{\mathrm{2}} ?{way}\:{not}\::{a},{b},{c}? \\ $$
Commented by RasheedSindhi last updated on 30/May/17
Actually my first figure was somewhat wrong! And mrW1 commented on that picture.
$$\mathrm{Actually}\:\mathrm{my}\:\mathrm{first}\:\mathrm{figure}\:\mathrm{was} \\ $$$$\mathrm{somewhat}\:\mathrm{wrong}!\:\mathrm{And}\:\mathrm{mrW1} \\ $$$$\mathrm{commented}\:\mathrm{on}\:\mathrm{that}\:\mathrm{picture}. \\ $$
Commented by mrW1 last updated on 30/May/17
to prakash: that′s what I wonder. 2 cylinders always have 2 intersection lines (curves). but the third cylinder doesn′t always intersect these 2 lines. for example if c is very small or very big in relation to a and b, see case 1 and 3 in picture.
$${to}\:{prakash}: \\ $$$${that}'{s}\:{what}\:{I}\:{wonder}.\:\mathrm{2}\:{cylinders}\:{always} \\ $$$${have}\:\mathrm{2}\:{intersection}\:{lines}\:\left({curves}\right). \\ $$$${but}\:{the}\:{third}\:{cylinder}\:{doesn}'{t}\:{always} \\ $$$${intersect}\:{these}\:\mathrm{2}\:{lines}.\:{for}\:{example} \\ $$$${if}\:{c}\:{is}\:{very}\:{small}\:{or}\:{very}\:{big}\:{in}\:{relation} \\ $$$${to}\:{a}\:{and}\:{b},\:{see}\:{case}\:\mathrm{1}\:{and}\:\mathrm{3}\:{in}\:{picture}. \\ $$
Commented by mrW1 last updated on 30/May/17
Commented by Tawa11 last updated on 15/Jan/22
Nice one sirs.
$$\mathrm{Nice}\:\mathrm{one}\:\mathrm{sirs}. \\ $$
Commented by prakash jain last updated on 15/Jan/22
Great to hear from you Tawa. Long time since we worked these questions
$$\mathrm{Great}\:\mathrm{to}\:\mathrm{hear}\:\mathrm{from}\:\mathrm{you}\:\mathrm{Tawa}. \\ $$$$\mathrm{Long}\:\mathrm{time}\:\mathrm{since}\:\mathrm{we}\:\mathrm{worked}\:\mathrm{these} \\ $$$$\mathrm{questions} \\ $$
Answered by RasheedSindhi last updated on 30/May/17
x^2 +y^2 +xy=a^2 ................(i) y^2 +z^2 +yz=b^2 ................(ii) z^2 +x^2 +zx=c^2 ................(iii) (i)−(ii): x^2 −z^2 +xy−yz=a^2 −b^2 (x−z)(x+z)+y(x−z)=a^2 −b^2 (x−z)(x+y+z)=a^2 −b^2 ......(iv) (iii)−(ii): x^2 −y^2 +xz−yz=c^2 −b^2 (x−y)(x+y)+z(x−y)=c^2 −b^2 (x−y)(x+y+z)=c^2 −b^2 .......(v) (v)/(iv): ((x−y)/(x−z))=((c^2 −b^2 )/(a^2 −b^2 )) x−y=((c^2 −b^2 )/(a^2 −b^2 ))(x−z) x−((c^2 −b^2 )/(a^2 −b^2 ))x=y−((c^2 −b^2 )/(a^2 −b^2 ))z x(1−((c^2 −b^2 )/(a^2 −b^2 )))=y−((c^2 −b^2 )/(a^2 −b^2 ))z x(((a^2 −b^2 −c^2 +b^2 )/(a^2 −b^2 )))=((y(a^2 −b^2 )−z(c^2 −b^2 ))/(a^2 −b^2 )) x(a^2 −c^2 )=y(a^2 −b^2 )−z(c^2 −b^2 ) x=((y(a^2 −b^2 )−z(c^2 −b^2 ))/(a^2 −c^2 )) Substituting in (v) [or in(iv)] (((y(a^2 −b^2 )−z(c^2 −b^2 ))/(a^2 −c^2 ))−y)(((y(a^2 −b^2 )−z(c^2 −b^2 ))/(a^2 −c^2 ))+y+z)=c^2 −b^2 (((y(a^2 −b^2 )−z(c^2 −b^2 )−y(a^2 −c^2 ))/(a^2 −c^2 )))(((y(a^2 −b^2 )−z(c^2 −b^2 )+y(a^2 −c^2 )+z(a^2 −c^2 ))/(a^2 −c^2 )))=c^2 −b^2 {y(c^2 −b^2 )−z(c^2 −b^2 )}{y(2a^2 −b^2 −c^2 )+z(a^2 +b^2 −2c^2 }=(c^2 −b^2 )(a^2 −c^2 )^2 (c^2 −b^2 )(y−z){y(2a^2 −b^2 −c^2 )+z(a^2 +b^2 −2c^2 }−(c^2 −b^2 )(a^2 −c^2 )^2 =0 (c^2 −b^2 ){(y−z){y(2a^2 −b^2 −c^2 )+z(a^2 +b^2 −2c^2 }−(a^2 −c^2 )^2 }=0 (c^2 −b^2 )=0∣{(y−z){y(2a^2 −b^2 −c^2 )+z(a^2 +b^2 −2c^2 }−(a^2 −c^2 )^2 }=0 b=c ∣(y−z){y(2a^2 −b^2 −c^2 )+z(a^2 +b^2 −2c^2 }−(a^2 −c^2 )^2 =0 (y−z){y(2a^2 −b^2 −c^2 )+z(a^2 +b^2 −2c^2 }=(a^2 −c^2 )^2 From (ii) y^2 +yz+z^2 −b^2 =0 y=((−z±(√(z^2 −4(z^2 −b^2 ))))/2) (((−z±(√(z^2 −4(z^2 −b^2 ))))/2)−z){(((−z±(√(z^2 −4(z^2 −b^2 ))))/2))(2a^2 −b^2 −c^2 )+z(a^2 +b^2 −2c^2 )}=(a^2 −c^2 )^2 (((−z±(√(z^2 −4(z^2 −b^2 )))−2z)/2)){(((−z±(√(z^2 −4(z^2 −b^2 ))))/2))(2a^2 −b^2 −c^2 )+z(a^2 +b^2 −2c^2 )}=(a^2 −c^2 )^2 Too complicated to solve for z
$$\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} +\mathrm{xy}=\mathrm{a}^{\mathrm{2}} …………….\left(\mathrm{i}\right) \\ $$$$\mathrm{y}^{\mathrm{2}} +\mathrm{z}^{\mathrm{2}} +\mathrm{yz}=\mathrm{b}^{\mathrm{2}} …………….\left(\mathrm{ii}\right) \\ $$$$\mathrm{z}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} +\mathrm{zx}=\mathrm{c}^{\mathrm{2}} …………….\left(\mathrm{iii}\right) \\ $$$$\left(\mathrm{i}\right)−\left(\mathrm{ii}\right): \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{z}^{\mathrm{2}} +\mathrm{xy}−\mathrm{yz}=\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \\ $$$$\left(\mathrm{x}−\mathrm{z}\right)\left(\mathrm{x}+\mathrm{z}\right)+\mathrm{y}\left(\mathrm{x}−\mathrm{z}\right)=\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \\ $$$$\left(\mathrm{x}−\mathrm{z}\right)\left(\mathrm{x}+\mathrm{y}+\mathrm{z}\right)=\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} ……\left(\mathrm{iv}\right) \\ $$$$\left(\mathrm{iii}\right)−\left(\mathrm{ii}\right): \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} +\mathrm{xz}−\mathrm{yz}=\mathrm{c}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \\ $$$$\left(\mathrm{x}−\mathrm{y}\right)\left(\mathrm{x}+\mathrm{y}\right)+\mathrm{z}\left(\mathrm{x}−\mathrm{y}\right)=\mathrm{c}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \\ $$$$\left(\mathrm{x}−\mathrm{y}\right)\left(\mathrm{x}+\mathrm{y}+\mathrm{z}\right)=\mathrm{c}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} …….\left(\mathrm{v}\right) \\ $$$$\left(\mathrm{v}\right)/\left(\mathrm{iv}\right): \\ $$$$\frac{\mathrm{x}−\mathrm{y}}{\mathrm{x}−\mathrm{z}}=\frac{\mathrm{c}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} } \\ $$$$\mathrm{x}−\mathrm{y}=\frac{\mathrm{c}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} }\left(\mathrm{x}−\mathrm{z}\right) \\ $$$$\mathrm{x}−\frac{\mathrm{c}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} }\mathrm{x}=\mathrm{y}−\frac{\mathrm{c}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} }\mathrm{z} \\ $$$$\mathrm{x}\left(\mathrm{1}−\frac{\mathrm{c}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} }\right)=\mathrm{y}−\frac{\mathrm{c}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} }\mathrm{z} \\ $$$$\mathrm{x}\left(\frac{\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} −\mathrm{c}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} }\right)=\frac{\mathrm{y}\left(\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)−\mathrm{z}\left(\mathrm{c}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)}{\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} } \\ $$$$\mathrm{x}\left(\mathrm{a}^{\mathrm{2}} −\mathrm{c}^{\mathrm{2}} \right)=\mathrm{y}\left(\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)−\mathrm{z}\left(\mathrm{c}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right) \\ $$$$\mathrm{x}=\frac{\mathrm{y}\left(\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)−\mathrm{z}\left(\mathrm{c}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)}{\mathrm{a}^{\mathrm{2}} −\mathrm{c}^{\mathrm{2}} } \\ $$$$\mathrm{Substituting}\:\mathrm{in}\:\left(\mathrm{v}\right)\:\left[\mathrm{or}\:\mathrm{in}\left(\mathrm{iv}\right)\right] \\ $$$$\left(\frac{\mathrm{y}\left(\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)−\mathrm{z}\left(\mathrm{c}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)}{\mathrm{a}^{\mathrm{2}} −\mathrm{c}^{\mathrm{2}} }−\mathrm{y}\right)\left(\frac{\mathrm{y}\left(\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)−\mathrm{z}\left(\mathrm{c}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)}{\mathrm{a}^{\mathrm{2}} −\mathrm{c}^{\mathrm{2}} }+\mathrm{y}+\mathrm{z}\right)=\mathrm{c}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \\ $$$$\left(\frac{\mathrm{y}\left(\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)−\mathrm{z}\left(\mathrm{c}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)−\mathrm{y}\left(\mathrm{a}^{\mathrm{2}} −\mathrm{c}^{\mathrm{2}} \right)}{\mathrm{a}^{\mathrm{2}} −\mathrm{c}^{\mathrm{2}} }\right)\left(\frac{\mathrm{y}\left(\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)−\mathrm{z}\left(\mathrm{c}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)+\mathrm{y}\left(\mathrm{a}^{\mathrm{2}} −\mathrm{c}^{\mathrm{2}} \right)+\mathrm{z}\left(\mathrm{a}^{\mathrm{2}} −\mathrm{c}^{\mathrm{2}} \right)}{\mathrm{a}^{\mathrm{2}} −\mathrm{c}^{\mathrm{2}} }\right)=\mathrm{c}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \\ $$$$\left\{\mathrm{y}\left(\mathrm{c}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)−\mathrm{z}\left(\mathrm{c}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)\right\}\left\{\mathrm{y}\left(\mathrm{2a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} −\mathrm{c}^{\mathrm{2}} \right)+\mathrm{z}\left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} −\mathrm{2c}^{\mathrm{2}} \right\}=\left(\mathrm{c}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)\left(\mathrm{a}^{\mathrm{2}} −\mathrm{c}^{\mathrm{2}} \right)^{\mathrm{2}} \right. \\ $$$$\left(\mathrm{c}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)\left(\mathrm{y}−\mathrm{z}\right)\left\{\mathrm{y}\left(\mathrm{2a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} −\mathrm{c}^{\mathrm{2}} \right)+\mathrm{z}\left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} −\mathrm{2c}^{\mathrm{2}} \right\}−\left(\mathrm{c}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)\left(\mathrm{a}^{\mathrm{2}} −\mathrm{c}^{\mathrm{2}} \right)^{\mathrm{2}} =\mathrm{0}\right. \\ $$$$\left(\mathrm{c}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)\left\{\left(\mathrm{y}−\mathrm{z}\right)\left\{\mathrm{y}\left(\mathrm{2a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} −\mathrm{c}^{\mathrm{2}} \right)+\mathrm{z}\left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} −\mathrm{2c}^{\mathrm{2}} \right\}−\left(\mathrm{a}^{\mathrm{2}} −\mathrm{c}^{\mathrm{2}} \right)^{\mathrm{2}} \right\}=\mathrm{0}\right. \\ $$$$\left(\mathrm{c}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)=\mathrm{0}\mid\left\{\left(\mathrm{y}−\mathrm{z}\right)\left\{\mathrm{y}\left(\mathrm{2a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} −\mathrm{c}^{\mathrm{2}} \right)+\mathrm{z}\left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} −\mathrm{2c}^{\mathrm{2}} \right\}−\left(\mathrm{a}^{\mathrm{2}} −\mathrm{c}^{\mathrm{2}} \right)^{\mathrm{2}} \right\}=\mathrm{0}\right. \\ $$$$\mathrm{b}=\mathrm{c}\:\mid\left(\mathrm{y}−\mathrm{z}\right)\left\{\mathrm{y}\left(\mathrm{2a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} −\mathrm{c}^{\mathrm{2}} \right)+\mathrm{z}\left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} −\mathrm{2c}^{\mathrm{2}} \right\}−\left(\mathrm{a}^{\mathrm{2}} −\mathrm{c}^{\mathrm{2}} \right)^{\mathrm{2}} =\mathrm{0}\right. \\ $$$$\left(\mathrm{y}−\mathrm{z}\right)\left\{\mathrm{y}\left(\mathrm{2a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} −\mathrm{c}^{\mathrm{2}} \right)+\mathrm{z}\left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} −\mathrm{2c}^{\mathrm{2}} \right\}=\left(\mathrm{a}^{\mathrm{2}} −\mathrm{c}^{\mathrm{2}} \right)^{\mathrm{2}} \right. \\ $$$$\mathrm{From}\:\left(\mathrm{ii}\right)\:\mathrm{y}^{\mathrm{2}} +\mathrm{yz}+\mathrm{z}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{y}=\frac{−\mathrm{z}\pm\sqrt{\mathrm{z}^{\mathrm{2}} −\mathrm{4}\left(\mathrm{z}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)}}{\mathrm{2}} \\ $$$$\left(\frac{−\mathrm{z}\pm\sqrt{\mathrm{z}^{\mathrm{2}} −\mathrm{4}\left(\mathrm{z}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)}}{\mathrm{2}}−\mathrm{z}\right)\left\{\left(\frac{−\mathrm{z}\pm\sqrt{\mathrm{z}^{\mathrm{2}} −\mathrm{4}\left(\mathrm{z}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)}}{\mathrm{2}}\right)\left(\mathrm{2a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} −\mathrm{c}^{\mathrm{2}} \right)+\mathrm{z}\left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} −\mathrm{2c}^{\mathrm{2}} \right)\right\}=\left(\mathrm{a}^{\mathrm{2}} −\mathrm{c}^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$$\left(\frac{−\mathrm{z}\pm\sqrt{\mathrm{z}^{\mathrm{2}} −\mathrm{4}\left(\mathrm{z}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)}−\mathrm{2z}}{\mathrm{2}}\right)\left\{\left(\frac{−\mathrm{z}\pm\sqrt{\mathrm{z}^{\mathrm{2}} −\mathrm{4}\left(\mathrm{z}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)}}{\mathrm{2}}\right)\left(\mathrm{2a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} −\mathrm{c}^{\mathrm{2}} \right)+\mathrm{z}\left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} −\mathrm{2c}^{\mathrm{2}} \right)\right\}=\left(\mathrm{a}^{\mathrm{2}} −\mathrm{c}^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$$\mathrm{Too}\:\mathrm{complicated}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{for}\:\mathrm{z} \\ $$$$ \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 29/May/17
hello mr Rasheed.thank you so much. but i need final answers.
$${hello}\:{mr}\:{Rasheed}.{thank}\:{you}\:{so}\:{much}. \\ $$$${but}\:{i}\:{need}\:{final}\:{answers}. \\ $$
Commented by ajfour last updated on 30/May/17
Sir, kindly see my view to the solution of this question in Q.14306.
$${Sir},\:{kindly}\:{see}\:{my}\:{view}\:{to}\:{the}\:{solution} \\ $$$${of}\:{this}\:{question}\:{in}\:{Q}.\mathrm{14306}. \\ $$
Commented by RasheedSindhi last updated on 29/May/17
⊺hank you behi,I am trying of my best!
$$\intercal\mathrm{hank}\:\mathrm{you}\:\mathrm{behi},\mathrm{I}\:\mathrm{am}\:\mathrm{trying}\:\mathrm{of} \\ $$$$\mathrm{my}\:\mathrm{best}! \\ $$
Commented by prakash jain last updated on 29/May/17
((x−y)/(x−z))=((c^2 −b^2 )/(a^2 −b^2 )) x(a^2 −b^2 −c^2 +b^2 )=y(a^2 −b^2 )+z(b^2 −c^2 ) x(a^2 −c^2 )=y(a^2 −b^2 )+z(b^2 −c^2 ) (i) y=kx,z=lx (a^2 −c^2 )=k(a^2 −b^2 )+l(b^2 −c^2 ) ⇒l=((a^2 −c^2 )/(b^2 −c^2 ))+((a^2 −b^2 )/(b^2 −c^2 ))k (i) x^2 (k^2 +k+1)=a^2 x^2 (k^2 +kl+1)=b^2 x^2 (l^2 +l+1)=c^2 ((k^2 +k+1)/(l^2 +l+1))=(a^2 /c^2 ) subtituting value of l from (i) (c^2 /a^2 )(k^2 +k+1)=[((a^2 −c^2 )/(b^2 −c^2 ))+((a^2 −b^2 )/(b^2 −c^2 ))k]^2 +[((a^2 −c^2 )/(b^2 −c^2 ))+((a^2 −b^2 )/(b^2 −c^2 ))k]+1 now we get a quadratic in k. a^2 −c^2 =u a^2 −b^2 =v ((a^2 −u)/a^2 )(k^2 +k+1)=[(u/(u−v))+(v/(u−v))k]^2 +[(u/(u−v))+(v/(u−v))k]+1 (1/a^2 )(u−v)^2 (a^2 −u)(k^2 +k+1) =(u+vk)^2 +(u−v)(u+vk)+(u−v)^2 It is a quadratic but not a simple answer. once we get k we can compute l and x.
$$\frac{{x}−{y}}{{x}−{z}}=\frac{{c}^{\mathrm{2}} −{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} } \\ $$$${x}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} −{c}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)={y}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)+{z}\left({b}^{\mathrm{2}} −{c}^{\mathrm{2}} \right) \\ $$$${x}\left({a}^{\mathrm{2}} −{c}^{\mathrm{2}} \right)={y}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)+{z}\left({b}^{\mathrm{2}} −{c}^{\mathrm{2}} \right)\:\:\left({i}\right) \\ $$$${y}={kx},{z}={lx} \\ $$$$\left({a}^{\mathrm{2}} −{c}^{\mathrm{2}} \right)={k}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)+{l}\left({b}^{\mathrm{2}} −{c}^{\mathrm{2}} \right) \\ $$$$\Rightarrow{l}=\frac{{a}^{\mathrm{2}} −{c}^{\mathrm{2}} }{{b}^{\mathrm{2}} −{c}^{\mathrm{2}} }+\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{{b}^{\mathrm{2}} −{c}^{\mathrm{2}} }{k}\:\:\:\:\left({i}\right) \\ $$$${x}^{\mathrm{2}} \left({k}^{\mathrm{2}} +{k}+\mathrm{1}\right)={a}^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} \left({k}^{\mathrm{2}} +{kl}+\mathrm{1}\right)={b}^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} \left({l}^{\mathrm{2}} +{l}+\mathrm{1}\right)={c}^{\mathrm{2}} \\ $$$$\frac{{k}^{\mathrm{2}} +{k}+\mathrm{1}}{{l}^{\mathrm{2}} +{l}+\mathrm{1}}=\frac{{a}^{\mathrm{2}} }{{c}^{\mathrm{2}} } \\ $$$${subtituting}\:{value}\:{of}\:{l}\:{from}\:\left({i}\right) \\ $$$$\frac{{c}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\left({k}^{\mathrm{2}} +{k}+\mathrm{1}\right)=\left[\frac{{a}^{\mathrm{2}} −{c}^{\mathrm{2}} }{{b}^{\mathrm{2}} −{c}^{\mathrm{2}} }+\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{{b}^{\mathrm{2}} −{c}^{\mathrm{2}} }{k}\right]^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:+\left[\frac{{a}^{\mathrm{2}} −{c}^{\mathrm{2}} }{{b}^{\mathrm{2}} −{c}^{\mathrm{2}} }+\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{{b}^{\mathrm{2}} −{c}^{\mathrm{2}} }{k}\right]+\mathrm{1} \\ $$$${now}\:{we}\:{get}\:{a}\:{quadratic}\:{in}\:{k}. \\ $$$${a}^{\mathrm{2}} −{c}^{\mathrm{2}} ={u} \\ $$$${a}^{\mathrm{2}} −{b}^{\mathrm{2}} ={v} \\ $$$$\frac{{a}^{\mathrm{2}} −{u}}{{a}^{\mathrm{2}} }\left({k}^{\mathrm{2}} +{k}+\mathrm{1}\right)=\left[\frac{{u}}{{u}−{v}}+\frac{{v}}{{u}−{v}}{k}\right]^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:+\left[\frac{{u}}{{u}−{v}}+\frac{{v}}{{u}−{v}}{k}\right]+\mathrm{1} \\ $$$$\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\left({u}−{v}\right)^{\mathrm{2}} \left({a}^{\mathrm{2}} −{u}\right)\left({k}^{\mathrm{2}} +{k}+\mathrm{1}\right) \\ $$$$\:\:\:=\left({u}+{vk}\right)^{\mathrm{2}} +\left({u}−{v}\right)\left({u}+{vk}\right)+\left({u}−{v}\right)^{\mathrm{2}} \\ $$$$\mathrm{It}\:\mathrm{is}\:\mathrm{a}\:\mathrm{quadratic}\:\mathrm{but}\:\mathrm{not}\:\mathrm{a}\:\mathrm{simple} \\ $$$$\mathrm{answer}. \\ $$$$\mathrm{once}\:\mathrm{we}\:\mathrm{get}\:{k}\:\mathrm{we}\:\mathrm{can}\:\mathrm{compute}\:{l}\:\mathrm{and} \\ $$$${x}. \\ $$
Commented by ajfour last updated on 29/May/17
thanks, all the best .
$${thanks},\:{all}\:{the}\:{best}\:. \\ $$
Commented by prakash jain last updated on 29/May/17
There is no simple solution. However there will be mutiple solution since equation are quadratic.
$$\mathrm{There}\:\mathrm{is}\:\mathrm{no}\:\mathrm{simple}\:\mathrm{solution}. \\ $$$$\mathrm{However}\:\mathrm{there}\:\mathrm{will}\:\mathrm{be}\:\mathrm{mutiple} \\ $$$$\mathrm{solution}\:\mathrm{since}\:\mathrm{equation}\:\mathrm{are}\:\mathrm{quadratic}. \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 30/May/17
hello mr Ajfour.i dont think x=y=z can be a solution for this system. x=y⇒3x^2 =a^2 ⇒x=(a/( (√3))) (a^2 /3)+z^2 +z(a/( (√3)))=c^2 . this equation cant lie to z=(a/( (√3))). thanks.
$${hello}\:{mr}\:{Ajfour}.{i}\:{dont}\:{think}\:{x}={y}={z} \\ $$$${can}\:{be}\:{a}\:{solution}\:{for}\:{this}\:{system}. \\ $$$${x}={y}\Rightarrow\mathrm{3}{x}^{\mathrm{2}} ={a}^{\mathrm{2}} \Rightarrow{x}=\frac{{a}}{\:\sqrt{\mathrm{3}}} \\ $$$$\frac{{a}^{\mathrm{2}} }{\mathrm{3}}+{z}^{\mathrm{2}} +{z}\frac{{a}}{\:\sqrt{\mathrm{3}}}={c}^{\mathrm{2}} \:.\:{this}\:{equation}\:{cant}\: \\ $$$${lie}\:{to}\:{z}=\frac{{a}}{\:\sqrt{\mathrm{3}}}.\:\:\:{thanks}. \\ $$$$ \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 29/May/17
thanks dear mr Rasheed.your try is so beautiful.thank you and other my best friends in this forum. god bless you all. after all words,.... there is some days that mrW1, is absent.i hope he is in safe and health.
$${thanks}\:{dear}\:{mr}\:{Rasheed}.{your}\:{try}\:{is} \\ $$$${so}\:{beautiful}.{thank}\:{you}\:{and}\:{other}\: \\ $$$${my}\:{best}\:{friends}\:{in}\:{this}\:{forum}. \\ $$$${god}\:{bless}\:{you}\:{all}. \\ $$$${after}\:{all}\:{words},….\:{there}\:{is}\:{some}\:{days}\:{that}\:{mrW}\mathrm{1}, \\ $$$${is}\:{absent}.{i}\:{hope}\:{he}\:{is}\:{in}\:{safe}\:{and}\:{health}. \\ $$$$ \\ $$
Commented by mrW1 last updated on 29/May/17
Thank you dear friend for your care! Every thing is ok with me.
$${Thank}\:{you}\:{dear}\:{friend}\:{for}\:{your}\:{care}!\: \\ $$$${Every}\:{thing}\:{is}\:{ok}\:{with}\:{me}. \\ $$
Commented by prakash jain last updated on 29/May/17
I added a new question 14211 with numbers for a^2 ,b^2 ,c^2 . The method gives the result but but calculators needed.
$$\mathrm{I}\:\mathrm{added}\:\mathrm{a}\:\mathrm{new}\:\mathrm{question}\:\mathrm{14211} \\ $$$$\mathrm{with}\:\mathrm{numbers}\:\mathrm{for}\:{a}^{\mathrm{2}} ,{b}^{\mathrm{2}} ,{c}^{\mathrm{2}} . \\ $$$$\mathrm{The}\:\mathrm{method}\:\mathrm{gives}\:\mathrm{the}\:\mathrm{result}\:\mathrm{but} \\ $$$$\mathrm{but}\:\mathrm{calculators}\:\mathrm{needed}. \\ $$
Commented by mrW1 last updated on 30/May/17
Some thoughts of mine to this question: In xy−plane x^2 +y^2 =a^2 is a circle. In xyz−space it is a cylinder whose axis is the z−axis. In the same way y^2 +z^2 =b^2 and z^2 +x^2 =c^2 are also cylinder in the xyz−space whose axis is x−axis and y−axis respectively. The solutions of { ((x^2 +y^2 =a^2 )),((y^2 +z^2 =b^2 )),((z^2 +x^2 =c^2 )) :} are the intersection points of theses 3 cylinders. Depending on a,b,c we have several solutions or no solution. In xy−plane x^2 +y^2 +xy=a^2 is an ellipse. In xyz−space it is also a cylinder parallel to z−axis. The solutions of { ((x^2 +y^2 +xy=a^2 )),((y^2 +z^2 +yz=b^2 )),((z^2 +x^2 +zx=c^2 )) :} are the intersection points of the 3 cylinders. Depending on a,b,c there could be several solutions or no solution.
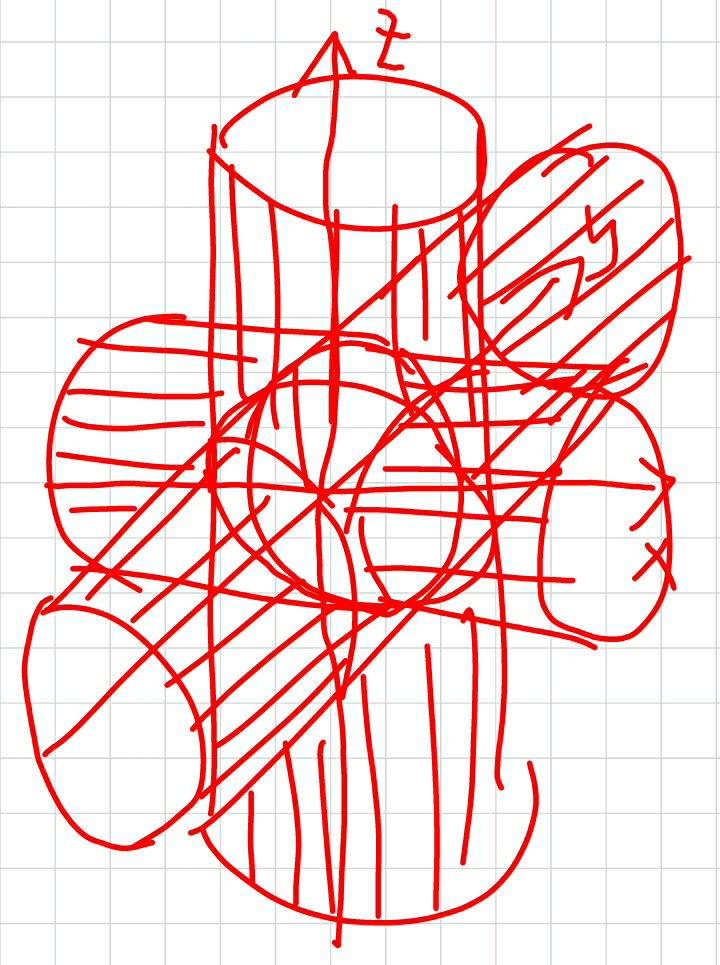
$${Some}\:{thoughts}\:{of}\:{mine}\:{to}\:{this}\:{question}: \\ $$$$ \\ $$$${In}\:{xy}−{plane}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={a}^{\mathrm{2}} \:{is}\:{a}\:{circle}.\:{In} \\ $$$${xyz}−{space}\:{it}\:{is}\:{a}\:{cylinder}\:{whose}\:{axis} \\ $$$${is}\:{the}\:{z}−{axis}. \\ $$$${In}\:{the}\:{same}\:{way}\:{y}^{\mathrm{2}} +{z}^{\mathrm{2}} ={b}^{\mathrm{2}} \:{and}\: \\ $$$${z}^{\mathrm{2}} +{x}^{\mathrm{2}} ={c}^{\mathrm{2}} \:{are}\:{also}\:{cylinder}\:{in}\:{the} \\ $$$${xyz}−{space}\:{whose}\:{axis}\:{is}\:{x}−{axis}\:{and} \\ $$$${y}−{axis}\:{respectively}. \\ $$$${The}\:{solutions}\:{of}\: \\ $$$$\begin{cases}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={a}^{\mathrm{2}} }\\{{y}^{\mathrm{2}} +{z}^{\mathrm{2}} ={b}^{\mathrm{2}} }\\{{z}^{\mathrm{2}} +{x}^{\mathrm{2}} ={c}^{\mathrm{2}} }\end{cases} \\ $$$${are}\:{the}\:{intersection}\:{points}\:{of}\:{theses} \\ $$$$\mathrm{3}\:{cylinders}.\:{Depending}\:{on}\:{a},{b},{c}\:{we} \\ $$$${have}\:{several}\:{solutions}\:{or}\:{no}\:{solution}. \\ $$$$ \\ $$$${In}\:{xy}−{plane}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{xy}={a}^{\mathrm{2}} \:{is}\:{an}\:{ellipse}. \\ $$$${In}\:{xyz}−{space}\:{it}\:{is}\:{also}\:{a}\:{cylinder} \\ $$$${parallel}\:{to}\:{z}−{axis}. \\ $$$${The}\:{solutions}\:{of} \\ $$$$\begin{cases}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{xy}={a}^{\mathrm{2}} }\\{{y}^{\mathrm{2}} +{z}^{\mathrm{2}} +{yz}={b}^{\mathrm{2}} }\\{{z}^{\mathrm{2}} +{x}^{\mathrm{2}} +{zx}={c}^{\mathrm{2}} }\end{cases} \\ $$$${are}\:{the}\:{intersection}\:{points}\:{of}\:{the}\:\mathrm{3} \\ $$$${cylinders}.\:{Depending}\:{on}\:{a},{b},{c}\:{there} \\ $$$${could}\:{be}\:{several}\:{solutions}\:{or}\:{no} \\ $$$${solution}. \\ $$
Commented by mrW1 last updated on 30/May/17
Commented by mrW1 last updated on 30/May/17
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 30/May/17
thank you dear mrW1.it is a nice method,if it give us some answers.
$${thank}\:{you}\:\:{dear}\:{mrW}\mathrm{1}.{it}\:{is}\:{a}\:{nice}\: \\ $$$${method},{if}\:{it}\:{give}\:{us}\:{some}\:{answers}. \\ $$
Commented by RasheedSindhi last updated on 30/May/17
G^(O^⌢ O^(⌢) ) D analysis mrW1!
$$\mathrm{G}^{\overset{\frown} {\mathcal{O}}\:\overset{\frown} {\mathcal{O}}} \mathrm{D}\:\:\mathrm{analysis}\:\mathrm{mrW1}! \\ $$
Commented by prakash jain last updated on 30/May/17
if a=b=c then x=y=z x=y=z=(a/( (√3)))
$$\mathrm{if}\:{a}={b}={c}\:\mathrm{then}\:{x}={y}={z} \\ $$$${x}={y}={z}=\frac{{a}}{\:\sqrt{\mathrm{3}}} \\ $$
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 31/May/17
we can assume that: x,y,z are segments in triangle ABC,whit sides of:a,b,c such that:∠ADB=∠BDC=∠CDA=120^• . now we have: (see picture below⇓) x^2 +y^2 +xy=a^2 y^2 +z^2 +yz=b^2 z^2 +x^2 +xz=c^2 S=(1/2)xysin120+(1/2)yzsin120+(1/2)xzsin120= =((√3)/4)(xy+yz+xz)⇒xy+yz+zx=((4S)/( (√3))) 2Σx^2 +Σxy=Σa^2 ⇒2Σx^2 =Σa^2 −((4S)/( (√3))) ⇒Σx^2 =Σ(a^2 /2)−((2S)/( (√3))) (Σx)^2 =Σx^2 +2Σxy=Σ(a^2 /2)−((2S)/( (√3)))+2(((4S)/( (√3))))= =Σ(a^2 /2)+((6S)/( (√3)))=Σ(a^2 /2)+2(√3)S ⇒x+y+z=(√(Σ(a^2 /2)+2(√3)S)) (=m) 4S=(√((a+b+c)(a+b−c)(a+c−b)(b+c−a))) (x−z)(x+y+z)=a^2 −b^2 ⇒x−z=((a^2 −b^2 )/m) (y−x)(x+y+z)=b^2 −c^2 ⇒y−x=((b^2 −c^2 )/m) ⇒(y−x)−(x−z)=((2b^2 −(a^2 +c^2 ))/m)⇒ ⇒m−3x=((2b^2 −(a^2 +c^2 ))/m)⇒ x=((m^2 +a^2 +c^2 −2b^2 )/(3m)) m^2 +a^2 +c^2 −2b^2 =Σ(a^2 /2)+2(√3)S+a^2 +c^2 −2b^2 = =(1/2)(3a^2 +3c^2 −3b^2 +4(√3)S) ⇒x=((√3)/2).((4S+(√3)(a^2 +c^2 −b^2 ))/(3m)) x=(1/( (√6))).(((√((a+b+c)(a+b−c)(a+c−b)(b+c−a)))+(√3)(a^2 +c^2 −b^2 ))/( (√(a^2 +b^2 +c^2 +(√(3(a+b+c)(a+b−c)(a+c−b)(b+c−a))))))) x−z=((a^2 −b^2 )/m),y−z=((a^2 −c^2 )/m) ⇒m−3z=((2a^2 −(b^2 +c^2 ))/m)⇒z=((m^2 +b^2 +c^2 −2a^2 )/(3m)) m^2 +b^2 +c^2 −2a^2 =Σ(a^2 /2)+2(√3)S+b^2 +c^2 −2a^2 = =(1/2)(3b^2 +3c^2 −3a^2 +4(√3)S) ⇒z=((√3)/2).((4S+(√3)(b^2 +c^2 −a^2 ))/(3m)) ⇒z=(1/( (√6))).(((√((a+b+c)(a+b−c)(a+c−b)(b+c−a)))+(√3)(b^2 +c^2 −a^2 ))/( (√(a^2 +b^2 +c^2 +(√(3(a+b+c)(a+b−c)(a+c−b)(b+c−a))))))) y=m−(x+z)=m−((m^2 +a^2 +c^2 −2b^2 )/(3m))−((m^2 +b^2 +c^2 −2a^2 )/(3m))= =((3m^2 −m^2 −a^2 −c^2 +2b^2 −m^2 −b^2 −c^2 +2a^2 )/(3m))= ⇒y=((m^2 +a^2 +b^2 −2c^2 )/(3m)) m^2 +a^2 +b^2 −2c^2 =((a^2 +b^2 +c^2 )/2)+2(√3)S+a^2 +b^2 −2c^2 = =(1/2)(3a^2 +3b^2 −3c^2 +4(√3)S) ⇒y=((√3)/2).((4S+(√3)(a^2 +b^2 −c^2 ))/(3m)) ⇒y=(1/( (√6))).(((√((a+b+c)(a+b−c)(a+c−b)(b+c−a)))+(√3)(a^2 +b^2 −2c^2 ))/( (√(a^2 +b^2 +c^2 +(√(3(a+b+c)(a+b−c)(a+c−b)(b+c−a))))))) .■
$${we}\:{can}\:{assume}\:{that}:\:{x},{y},{z}\:{are}\:{segments} \\ $$$${in}\:{triangle}\:{ABC},{whit}\:{sides}\:{of}:{a},{b},{c} \\ $$$${such}\:{that}:\angle{ADB}=\angle{BDC}=\angle{CDA}=\mathrm{120}^{\bullet} . \\ $$$${now}\:{we}\:{have}:\:\left({see}\:{picture}\:{below}\Downarrow\right) \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{xy}={a}^{\mathrm{2}} \\ $$$${y}^{\mathrm{2}} +{z}^{\mathrm{2}} +{yz}={b}^{\mathrm{2}} \\ $$$${z}^{\mathrm{2}} +{x}^{\mathrm{2}} +{xz}={c}^{\mathrm{2}} \\ $$$${S}=\frac{\mathrm{1}}{\mathrm{2}}{xysin}\mathrm{120}+\frac{\mathrm{1}}{\mathrm{2}}{yzsin}\mathrm{120}+\frac{\mathrm{1}}{\mathrm{2}}{xzsin}\mathrm{120}= \\ $$$$=\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\left({xy}+{yz}+{xz}\right)\Rightarrow{xy}+{yz}+{zx}=\frac{\mathrm{4}{S}}{\:\sqrt{\mathrm{3}}} \\ $$$$\mathrm{2}\Sigma{x}^{\mathrm{2}} +\Sigma{xy}=\Sigma{a}^{\mathrm{2}} \Rightarrow\mathrm{2}\Sigma{x}^{\mathrm{2}} =\Sigma{a}^{\mathrm{2}} −\frac{\mathrm{4}{S}}{\:\sqrt{\mathrm{3}}} \\ $$$$\Rightarrow\Sigma{x}^{\mathrm{2}} =\Sigma\frac{{a}^{\mathrm{2}} }{\mathrm{2}}−\frac{\mathrm{2}{S}}{\:\sqrt{\mathrm{3}}} \\ $$$$\left(\Sigma{x}\right)^{\mathrm{2}} =\Sigma{x}^{\mathrm{2}} +\mathrm{2}\Sigma{xy}=\Sigma\frac{{a}^{\mathrm{2}} }{\mathrm{2}}−\frac{\mathrm{2}{S}}{\:\sqrt{\mathrm{3}}}+\mathrm{2}\left(\frac{\mathrm{4}{S}}{\:\sqrt{\mathrm{3}}}\right)= \\ $$$$=\Sigma\frac{{a}^{\mathrm{2}} }{\mathrm{2}}+\frac{\mathrm{6}{S}}{\:\sqrt{\mathrm{3}}}=\Sigma\frac{{a}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{2}\sqrt{\mathrm{3}}{S} \\ $$$$\Rightarrow{x}+{y}+{z}=\sqrt{\Sigma\frac{{a}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{2}\sqrt{\mathrm{3}}{S}}\:\:\left(={m}\right) \\ $$$$\mathrm{4}{S}=\sqrt{\left({a}+{b}+{c}\right)\left({a}+{b}−{c}\right)\left({a}+{c}−{b}\right)\left({b}+{c}−{a}\right)} \\ $$$$\left({x}−{z}\right)\left({x}+{y}+{z}\right)={a}^{\mathrm{2}} −{b}^{\mathrm{2}} \Rightarrow{x}−{z}=\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{{m}} \\ $$$$\left({y}−{x}\right)\left({x}+{y}+{z}\right)={b}^{\mathrm{2}} −{c}^{\mathrm{2}} \Rightarrow{y}−{x}=\frac{{b}^{\mathrm{2}} −{c}^{\mathrm{2}} }{{m}} \\ $$$$\Rightarrow\left({y}−{x}\right)−\left({x}−{z}\right)=\frac{\mathrm{2}{b}^{\mathrm{2}} −\left({a}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)}{{m}}\Rightarrow \\ $$$$\Rightarrow{m}−\mathrm{3}{x}=\frac{\mathrm{2}{b}^{\mathrm{2}} −\left({a}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)}{{m}}\Rightarrow \\ $$$${x}=\frac{{m}^{\mathrm{2}} +{a}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}{b}^{\mathrm{2}} }{\mathrm{3}{m}} \\ $$$${m}^{\mathrm{2}} +{a}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}{b}^{\mathrm{2}} =\Sigma\frac{{a}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{2}\sqrt{\mathrm{3}}{S}+{a}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}{b}^{\mathrm{2}} = \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{3}{a}^{\mathrm{2}} +\mathrm{3}{c}^{\mathrm{2}} −\mathrm{3}{b}^{\mathrm{2}} +\mathrm{4}\sqrt{\mathrm{3}}{S}\right) \\ $$$$\Rightarrow{x}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}.\frac{\mathrm{4}{S}+\sqrt{\mathrm{3}}\left({a}^{\mathrm{2}} +{c}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)}{\mathrm{3}{m}} \\ $$$${x}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{6}}}.\frac{\sqrt{\left({a}+{b}+{c}\right)\left({a}+{b}−{c}\right)\left({a}+{c}−{b}\right)\left({b}+{c}−{a}\right)}+\sqrt{\mathrm{3}}\left({a}^{\mathrm{2}} +{c}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)}{\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +\sqrt{\mathrm{3}\left({a}+{b}+{c}\right)\left({a}+{b}−{c}\right)\left({a}+{c}−{b}\right)\left({b}+{c}−{a}\right)}}} \\ $$$${x}−{z}=\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{{m}},{y}−{z}=\frac{{a}^{\mathrm{2}} −{c}^{\mathrm{2}} }{{m}} \\ $$$$\Rightarrow{m}−\mathrm{3}{z}=\frac{\mathrm{2}{a}^{\mathrm{2}} −\left({b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)}{{m}}\Rightarrow{z}=\frac{{m}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}{a}^{\mathrm{2}} }{\mathrm{3}{m}} \\ $$$${m}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}{a}^{\mathrm{2}} =\Sigma\frac{{a}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{2}\sqrt{\mathrm{3}}{S}+{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}{a}^{\mathrm{2}} = \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{3}{b}^{\mathrm{2}} +\mathrm{3}{c}^{\mathrm{2}} −\mathrm{3}{a}^{\mathrm{2}} +\mathrm{4}\sqrt{\mathrm{3}}{S}\right) \\ $$$$\Rightarrow{z}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}.\frac{\mathrm{4}{S}+\sqrt{\mathrm{3}}\left({b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)}{\mathrm{3}{m}} \\ $$$$\Rightarrow\boldsymbol{{z}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{6}}}.\frac{\sqrt{\left(\boldsymbol{{a}}+\boldsymbol{{b}}+\boldsymbol{{c}}\right)\left(\boldsymbol{{a}}+\boldsymbol{{b}}−\boldsymbol{{c}}\right)\left(\boldsymbol{{a}}+\boldsymbol{{c}}−\boldsymbol{{b}}\right)\left(\boldsymbol{{b}}+\boldsymbol{{c}}−\boldsymbol{{a}}\right)}+\sqrt{\mathrm{3}}\left(\boldsymbol{{b}}^{\mathrm{2}} +\boldsymbol{{c}}^{\mathrm{2}} −\boldsymbol{{a}}^{\mathrm{2}} \right)}{\:\sqrt{\boldsymbol{{a}}^{\mathrm{2}} +\boldsymbol{{b}}^{\mathrm{2}} +\boldsymbol{{c}}^{\mathrm{2}} +\sqrt{\mathrm{3}\left(\boldsymbol{{a}}+\boldsymbol{{b}}+\boldsymbol{{c}}\right)\left(\boldsymbol{{a}}+\boldsymbol{{b}}−\boldsymbol{{c}}\right)\left(\boldsymbol{{a}}+\boldsymbol{{c}}−\boldsymbol{{b}}\right)\left(\boldsymbol{{b}}+\boldsymbol{{c}}−\boldsymbol{{a}}\right)}}} \\ $$$$\boldsymbol{{y}}=\boldsymbol{{m}}−\left(\boldsymbol{{x}}+\boldsymbol{{z}}\right)=\boldsymbol{{m}}−\frac{{m}^{\mathrm{2}} +{a}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}{b}^{\mathrm{2}} }{\mathrm{3}{m}}−\frac{{m}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}{a}^{\mathrm{2}} }{\mathrm{3}{m}}= \\ $$$$=\frac{\mathrm{3}{m}^{\mathrm{2}} −{m}^{\mathrm{2}} −{a}^{\mathrm{2}} −{c}^{\mathrm{2}} +\mathrm{2}{b}^{\mathrm{2}} −{m}^{\mathrm{2}} −{b}^{\mathrm{2}} −{c}^{\mathrm{2}} +\mathrm{2}{a}^{\mathrm{2}} }{\mathrm{3}{m}}= \\ $$$$\Rightarrow{y}=\frac{{m}^{\mathrm{2}} +{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{c}^{\mathrm{2}} }{\mathrm{3}{m}} \\ $$$${m}^{\mathrm{2}} +{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{c}^{\mathrm{2}} =\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{2}\sqrt{\mathrm{3}}{S}+{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{c}^{\mathrm{2}} = \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{3}{a}^{\mathrm{2}} +\mathrm{3}{b}^{\mathrm{2}} −\mathrm{3}{c}^{\mathrm{2}} +\mathrm{4}\sqrt{\mathrm{3}}{S}\right) \\ $$$$\Rightarrow{y}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}.\frac{\mathrm{4}{S}+\sqrt{\mathrm{3}}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{c}^{\mathrm{2}} \right)}{\mathrm{3}{m}} \\ $$$$\Rightarrow\boldsymbol{{y}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{6}}}.\frac{\sqrt{\left(\boldsymbol{{a}}+\boldsymbol{{b}}+\boldsymbol{{c}}\right)\left(\boldsymbol{{a}}+\boldsymbol{{b}}−\boldsymbol{{c}}\right)\left(\boldsymbol{{a}}+\boldsymbol{{c}}−\boldsymbol{{b}}\right)\left(\boldsymbol{{b}}+\boldsymbol{{c}}−\boldsymbol{{a}}\right)}+\sqrt{\mathrm{3}}\left(\boldsymbol{{a}}^{\mathrm{2}} +\boldsymbol{{b}}^{\mathrm{2}} −\mathrm{2}\boldsymbol{{c}}^{\mathrm{2}} \right)}{\:\sqrt{\boldsymbol{{a}}^{\mathrm{2}} +\boldsymbol{{b}}^{\mathrm{2}} +\boldsymbol{{c}}^{\mathrm{2}} +\sqrt{\mathrm{3}\left(\boldsymbol{{a}}+\boldsymbol{{b}}+\boldsymbol{{c}}\right)\left(\boldsymbol{{a}}+\boldsymbol{{b}}−\boldsymbol{{c}}\right)\left(\boldsymbol{{a}}+\boldsymbol{{c}}−\boldsymbol{{b}}\right)\left(\boldsymbol{{b}}+\boldsymbol{{c}}−\boldsymbol{{a}}\right)}}}\:.\blacksquare \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 30/May/17
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 31/May/17
try for a=2,b=3,c=4 x=((m^2 +a^2 +c^2 −2b^2 )/(3m)) y=((m^2 +a^2 +b^2 −2c^2 )/(3m)) z=((m^2 +b^2 +c^2 −2a^2 )/(3m)) m^2 =Σ(a^2 /2)+2(√3)S 4S=(√(9×1×5×3))=3(√(15))⇒S=((3(√(15)))/4)=2.9 m^2 =((29)/2)+2(√3)×2.9=24.55⇒m=±4.95 x=((24.55+2)/(±3×4.95))=((26.55)/(±14.85))=±1.78 y=((24.55−19)/(±14.85))=±((5.55)/(14.85))=±0.37 z=((24.55+17)/(±14.85))=((41.55)/(±14.85))=±2.79 .■
$${try}\:{for}\:{a}=\mathrm{2},{b}=\mathrm{3},{c}=\mathrm{4} \\ $$$${x}=\frac{{m}^{\mathrm{2}} +{a}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}{b}^{\mathrm{2}} }{\mathrm{3}{m}} \\ $$$${y}=\frac{{m}^{\mathrm{2}} +{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{c}^{\mathrm{2}} }{\mathrm{3}{m}} \\ $$$${z}=\frac{{m}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}{a}^{\mathrm{2}} }{\mathrm{3}{m}} \\ $$$${m}^{\mathrm{2}} =\Sigma\frac{{a}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{2}\sqrt{\mathrm{3}}{S} \\ $$$$\mathrm{4}{S}=\sqrt{\mathrm{9}×\mathrm{1}×\mathrm{5}×\mathrm{3}}=\mathrm{3}\sqrt{\mathrm{15}}\Rightarrow{S}=\frac{\mathrm{3}\sqrt{\mathrm{15}}}{\mathrm{4}}=\mathrm{2}.\mathrm{9} \\ $$$${m}^{\mathrm{2}} =\frac{\mathrm{29}}{\mathrm{2}}+\mathrm{2}\sqrt{\mathrm{3}}×\mathrm{2}.\mathrm{9}=\mathrm{24}.\mathrm{55}\Rightarrow{m}=\pm\mathrm{4}.\mathrm{95} \\ $$$${x}=\frac{\mathrm{24}.\mathrm{55}+\mathrm{2}}{\pm\mathrm{3}×\mathrm{4}.\mathrm{95}}=\frac{\mathrm{26}.\mathrm{55}}{\pm\mathrm{14}.\mathrm{85}}=\pm\mathrm{1}.\mathrm{78} \\ $$$${y}=\frac{\mathrm{24}.\mathrm{55}−\mathrm{19}}{\pm\mathrm{14}.\mathrm{85}}=\pm\frac{\mathrm{5}.\mathrm{55}}{\mathrm{14}.\mathrm{85}}=\pm\mathrm{0}.\mathrm{37} \\ $$$${z}=\frac{\mathrm{24}.\mathrm{55}+\mathrm{17}}{\pm\mathrm{14}.\mathrm{85}}=\frac{\mathrm{41}.\mathrm{55}}{\pm\mathrm{14}.\mathrm{85}}=\pm\mathrm{2}.\mathrm{79}\:\:.\blacksquare \\ $$
Commented by mrW1 last updated on 31/May/17
that′s perfect!
$${that}'{s}\:{perfect}! \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 31/May/17
if a=b=c m^2 =((3a^2 )/2)×2(√3).((a^2 (√3))/4)=((3a^2 )/2)+((3a^2 )/2)=3a^2 ⇒m=a(√3) x=y=z=((3a^2 +a^2 +a^2 −2a^2 )/(3a(√3)))=a((√3)/3) . in this solution we see that :system have only one set of answers.what do you think about another set(s)of answers?
$${if}\:{a}={b}={c} \\ $$$${m}^{\mathrm{2}} =\frac{\mathrm{3}{a}^{\mathrm{2}} }{\mathrm{2}}×\mathrm{2}\sqrt{\mathrm{3}}.\frac{{a}^{\mathrm{2}} \sqrt{\mathrm{3}}}{\mathrm{4}}=\frac{\mathrm{3}{a}^{\mathrm{2}} }{\mathrm{2}}+\frac{\mathrm{3}{a}^{\mathrm{2}} }{\mathrm{2}}=\mathrm{3}{a}^{\mathrm{2}} \\ $$$$\Rightarrow{m}={a}\sqrt{\mathrm{3}} \\ $$$${x}={y}={z}=\frac{\mathrm{3}{a}^{\mathrm{2}} +{a}^{\mathrm{2}} +{a}^{\mathrm{2}} −\mathrm{2}{a}^{\mathrm{2}} }{\mathrm{3}{a}\sqrt{\mathrm{3}}}={a}\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\:. \\ $$$${in}\:{this}\:{solution}\:{we}\:{see}\:{that}\::{system} \\ $$$${have}\:{only}\:{one}\:{set}\:{of}\:{answers}.{what} \\ $$$${do}\:{you}\:{think}\:{about}\:{another}\:{set}\left({s}\right){of} \\ $$$${answers}? \\ $$
Commented by mrW1 last updated on 31/May/17
you get a set of solution in this way: (u,v,w) with u=..... (what you write as x above) v=..... (what you write as y above) w=..... (what you write as z above) due to symmetry and ± sign the original equation system has following solution 12 sets: (x,y,z)=(u,v,w) (x,y,z)=(−u,−v,−w) (x,y,z)=(v,u,w) (x,y,z)=(−v,−u,−w) (x,y,z)=(w,u,v) (x,y,z)=(−w,−u,−v) (x,y,z)=(u,w,v) .....
$${you}\:{get}\:{a}\:{set}\:{of}\:{solution}\:{in}\:{this}\:{way}: \\ $$$$\left({u},{v},{w}\right)\:{with} \\ $$$${u}=…..\:\left({what}\:{you}\:{write}\:{as}\:{x}\:{above}\right) \\ $$$${v}=…..\:\left({what}\:{you}\:{write}\:{as}\:{y}\:{above}\right) \\ $$$${w}=…..\:\left({what}\:{you}\:{write}\:{as}\:{z}\:{above}\right) \\ $$$$ \\ $$$${due}\:{to}\:{symmetry}\:{and}\:\pm\:{sign}\:{the} \\ $$$${original}\:{equation}\:{system}\:{has} \\ $$$${following}\:{solution}\:\mathrm{12}\:{sets}: \\ $$$$\left({x},{y},{z}\right)=\left({u},{v},{w}\right) \\ $$$$\left({x},{y},{z}\right)=\left(−{u},−{v},−{w}\right) \\ $$$$\left({x},{y},{z}\right)=\left({v},{u},{w}\right) \\ $$$$\left({x},{y},{z}\right)=\left(−{v},−{u},−{w}\right) \\ $$$$\left({x},{y},{z}\right)=\left({w},{u},{v}\right) \\ $$$$\left({x},{y},{z}\right)=\left(−{w},−{u},−{v}\right) \\ $$$$\left({x},{y},{z}\right)=\left({u},{w},{v}\right) \\ $$$$….. \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 31/May/17
thank you dear mrW1.you are right. what do you think about ⇑this solution? we use geometry to solve, and my be, we lost some answers .
$${thank}\:{you}\:{dear}\:{mrW}\mathrm{1}.{you}\:{are}\:{right}. \\ $$$${what}\:{do}\:{you}\:{think}\:{about}\:\Uparrow{this}\:{solution}? \\ $$$${we}\:{use}\:{geometry}\:\:{to}\:{solve}, \\ $$$${and}\:{my}\:{be},\:{we}\:{lost}\:{some}\:{answers}\:. \\ $$
Commented by mrW1 last updated on 31/May/17
I don′t think we lost some answers in this way. Your solution is very nice. The most important idea to this solution is the geometric interpretation from Mr. Sindhi. Also a big thank to him!
$${I}\:{don}'{t}\:{think}\:{we}\:{lost}\:{some}\:{answers} \\ $$$${in}\:{this}\:{way}.\:{Your}\:{solution}\:{is}\:{very} \\ $$$${nice}.\:{The}\:{most}\:{important}\:{idea}\:{to} \\ $$$${this}\:{solution}\:{is}\:{the}\:{geometric} \\ $$$${interpretation}\:{from}\:{Mr}.\:{Sindhi}.\:{Also} \\ $$$${a}\:{big}\:{thank}\:{to}\:{him}! \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 31/May/17
thanks a lot.yes .mrW1,mr sindhi, mr prakash,mr Ajfour,all have the same part in solving this Q. i love you all my best friends.
$${thanks}\:{a}\:{lot}.{yes}\:.{mrW}\mathrm{1},{mr}\:{sindhi}, \\ $$$${mr}\:{prakash},{mr}\:{Ajfour},{all}\:{have}\:{the} \\ $$$${same}\:{part}\:{in}\:{solving}\:{this}\:{Q}. \\ $$$${i}\:{love}\:{you}\:{all}\:{my}\:{best}\:{friends}. \\ $$
Commented by RasheedSindhi last updated on 31/May/17
Thanks very much mrW1 and behi for encouraging/appreciating so much. I also love the answer of Mr^(?) /Miss^(?) behi!
$$\mathcal{T}{hanks}\:{very}\:{much}\:{mrW}\mathrm{1}\:\mathrm{and} \\ $$$$\mathrm{behi}\:\mathrm{for}\:\mathrm{encouraging}/\mathrm{appreciating} \\ $$$$\mathrm{so}\:\mathrm{much}.\:\mathrm{I}\:\mathrm{also}\:\mathrm{love}\:\mathrm{the}\:\mathrm{answer} \\ $$$$\mathrm{of}\:\overset{?} {\mathrm{Mr}}/\overset{?} {\mathrm{Miss}}\:\mathrm{behi}! \\ $$
Commented by RasheedSindhi last updated on 31/May/17
One thing more sir (mrW1) I want to learn from you that you′ve said here that the equation(x^2 +y^2 =a^2 ) in a plane represent circle(Ok!)and in space it represents cyllinder (Assuming Ok, because I am not experienced in 3d graph) But when you say that the equation(x^2 +y^2 +xy=a^2 ) is ellipse in plane(Ok) and cyllinder in space then I can′t understand! Shouldn′t be this cyllinder of elliptical type instead of normal circular cyllinder?
$$\mathrm{One}\:\mathrm{thing}\:\mathrm{more}\:\mathrm{sir}\:\left(\mathrm{mrW1}\right) \\ $$$$\mathrm{I}\:\mathrm{want}\:\mathrm{to}\:\mathrm{learn}\:\mathrm{from}\:\mathrm{you}\:\mathrm{that}\:\mathrm{you}'\mathrm{ve} \\ $$$$\mathrm{said}\:\mathrm{here}\:\mathrm{that}\:\mathrm{the}\:\mathrm{equation}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} =\mathrm{a}^{\mathrm{2}} \right) \\ $$$$\mathrm{in}\:\mathrm{a}\:\mathrm{plane}\:\mathrm{represent}\:\mathrm{circle}\left(\mathrm{Ok}!\right)\mathrm{and} \\ $$$$\mathrm{in}\:\mathrm{space}\:\mathrm{it}\:\mathrm{represents}\:\mathrm{cyllinder} \\ $$$$\left(\mathrm{Assuming}\:\mathrm{Ok},\:\mathrm{because}\:\mathrm{I}\:\mathrm{am}\right. \\ $$$$\left.\mathrm{not}\:\mathrm{experienced}\:\mathrm{in}\:\mathrm{3d}\:\mathrm{graph}\right) \\ $$$$\mathrm{But}\:\mathrm{when}\:\mathrm{you}\:\mathrm{say}\:\mathrm{that}\:\mathrm{the} \\ $$$$\mathrm{equation}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} +\mathrm{xy}=\mathrm{a}^{\mathrm{2}} \right)\:\mathrm{is} \\ $$$$\mathrm{ellipse}\:\mathrm{in}\:\mathrm{plane}\left(\mathrm{Ok}\right)\:\mathrm{and}\:\mathrm{cyllinder} \\ $$$$\mathrm{in}\:\mathrm{space}\:\mathrm{then}\:\mathrm{I}\:\mathrm{can}'\mathrm{t}\:\mathrm{understand}! \\ $$$$\mathrm{Shouldn}'\mathrm{t}\:\mathrm{be}\:\mathrm{this}\:\mathrm{cyllinder}\:\mathrm{of} \\ $$$$\mathrm{elliptical}\:\mathrm{type}\:\mathrm{instead}\:\mathrm{of}\:\mathrm{normal} \\ $$$$\mathrm{circular}\:\mathrm{cyllinder}? \\ $$
Commented by mrW1 last updated on 31/May/17
Yes. It is an oval cylinder.
$${Yes}.\:{It}\:{is}\:{an}\:{oval}\:{cylinder}. \\ $$
Commented by RasheedSindhi last updated on 31/May/17
Thanks!
$$\mathcal{T}{hanks}! \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 31/May/17
mr Rasheed! i am your first quistion mark!(hahaha) thanks.
$${mr}\:{Rasheed}!\:{i}\:{am}\:{your}\:{first}\:{quistion} \\ $$$${mark}!\left({hahaha}\right)\:{thanks}. \\ $$
Commented by RasheedSindhi last updated on 31/May/17
Of course ?behi Actually this question is a variable whose domain is {Mr, Miss} This question of the forum which has no number can be solved here only by you! hahaha...
$$\mathrm{Of}\:\mathrm{course} \\ $$$$?\mathrm{behi} \\ $$$$\mathrm{Actually}\:\mathrm{this}\:\mathrm{question}\:\mathrm{is}\:\mathrm{a} \\ $$$$\mathrm{variable}\:\mathrm{whose}\:\:\mathrm{domain}\:\mathrm{is} \\ $$$$\left\{\mathrm{Mr},\:\mathrm{Miss}\right\} \\ $$$$\mathrm{This}\:\mathrm{question}\:\mathrm{of}\:\mathrm{the}\:\mathrm{forum} \\ $$$$\mathrm{which}\:\mathrm{has}\:\mathrm{no}\:\mathrm{number}\:\mathrm{can}\: \\ $$$$\mathrm{be}\:\mathrm{solved}\:\mathrm{here}\:\mathrm{only}\:\mathrm{by}\:\mathrm{you}! \\ $$$$\mathrm{hahaha}… \\ $$
Commented by RasheedSindhi last updated on 31/May/17
If you solve then in Miss tawa′s words: God bless you sir! I really appreciate you.
$$\mathrm{If}\:\mathrm{you}\:\mathrm{solve}\:\mathrm{then}\:\mathrm{in}\:\mathrm{Miss}\:\mathrm{tawa}'\mathrm{s} \\ $$$$\mathrm{words}: \\ $$$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\boldsymbol{\mathrm{sir}}!\:\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{you}. \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 31/May/17
mr Rasheed! my name is:Amir i am from IRAN.have MB in structural enginering.now at age:40 BEHI,is the name of my son. i glad to see you and other my friends in this forum.the (lim)of my love to math is:∞!excuse me for my english, because i am week in it.
$${mr}\:{Rasheed}!\:{my}\:{name}\:{is}:{Amir} \\ $$$${i}\:{am}\:{from}\:{IRAN}.{have}\:{MB}\:{in} \\ $$$${structural}\:{enginering}.{now}\:{at}\:{age}:\mathrm{40} \\ $$$${BEHI},{is}\:{the}\:{name}\:{of}\:{my}\:{son}. \\ $$$${i}\:{glad}\:{to}\:{see}\:{you}\:{and}\:{other}\:{my}\:{friends} \\ $$$${in}\:{this}\:{forum}.{the}\:\left(\mathrm{lim}\right){of}\:{my}\:{love}\:{to} \\ $$$${math}\:{is}:\infty!{excuse}\:{me}\:{for}\:{my}\:{english}, \\ $$$${because}\:{i}\:{am}\:{week}\:{in}\:{it}. \\ $$
Commented by RasheedSindhi last updated on 01/Jun/17
HAPPY to be introduced with you! I ′m from Sindh, Pakistan. I ′m maths teacher in a high school. I also love maths and that′s the reason of my being in this fine forum! I learnt much from forum-friends and want to learn much more!
$$\mathcal{HAPPY}\:\:{to}\:{be}\:{introduced}\:{with} \\ $$$${you}!\:\mathcal{I}\:'{m}\:{from}\:{Sindh},\:{Pakistan}. \\ $$$$\mathcal{I}\:'{m}\:{maths}\:{teacher}\:{in}\:{a}\:{high} \\ $$$${school}.\:\mathcal{I}\:{also}\:{love}\:{maths}\:{and} \\ $$$${that}'{s}\:{the}\:{reason}\:{of}\:{my}\:{being} \\ $$$${in}\:{this}\:{fine}\:{forum}! \\ $$$$\mathcal{I}\:{learnt}\:{much}\:{from}\:{forum}-{friends} \\ $$$${and}\:{want}\:{to}\:{learn}\:{much}\:{more}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *