Question Number 14354 by tawa tawa last updated on 30/May/17

Answered by mrW1 last updated on 31/May/17
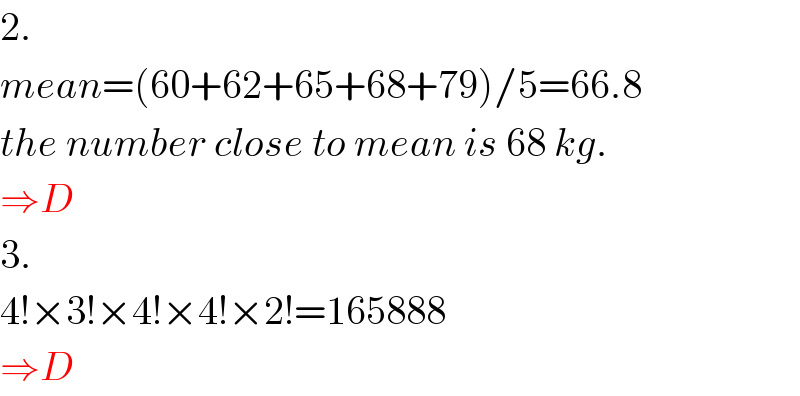
$$\mathrm{2}. \\ $$$${mean}=\left(\mathrm{60}+\mathrm{62}+\mathrm{65}+\mathrm{68}+\mathrm{79}\right)/\mathrm{5}=\mathrm{66}.\mathrm{8} \\ $$$${the}\:{number}\:{close}\:{to}\:{mean}\:{is}\:\mathrm{68}\:{kg}. \\ $$$$\Rightarrow{D} \\ $$$$\mathrm{3}. \\ $$$$\mathrm{4}!×\mathrm{3}!×\mathrm{4}!×\mathrm{4}!×\mathrm{2}!=\mathrm{165888} \\ $$$$\Rightarrow{D} \\ $$
Commented by mrW1 last updated on 31/May/17

$${Explanation}\:{to}\:{Q}\mathrm{2}. \\ $$$${n}\:{values}:\:{x}_{{i}} \\ $$$${mean}\:{m}=\frac{\mathrm{1}}{{n}}\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{x}_{{i}} \\ $$$${sum}\:{of}\:{squared}\:{devition}\:{from}\:{a}\:{value}\:{u} \\ $$$${is} \\ $$$${S}=\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\left({x}_{{i}} −{u}\right)^{\mathrm{2}} =\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\left({x}_{{i}} ^{\mathrm{2}} −\mathrm{2}{ux}_{{i}} +{u}^{\mathrm{2}} \right) \\ $$$$=\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{x}_{{i}} ^{\mathrm{2}} −\mathrm{2}{u}\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{x}_{{i}} +\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{u}^{\mathrm{2}} \\ $$$$=\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{x}_{{i}} ^{\mathrm{2}} −\mathrm{2}{unm}+{nu}^{\mathrm{2}} \\ $$$$=\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{x}_{{i}} ^{\mathrm{2}} −{nm}^{\mathrm{2}} +{nm}^{\mathrm{2}} −\mathrm{2}{unm}+{nu}^{\mathrm{2}} \\ $$$$=\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{x}_{{i}} ^{\mathrm{2}} −{nm}^{\mathrm{2}} +{n}\left({u}−{m}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{the}\:{smaller}\:{the}\:{difference}\:{between} \\ $$$${u}\:{and}\:{m}\:\left({i}.{e}.\:\mid{u}−{m}\mid\right),\:{the}\:{smaller}\:{the}\:{sum}\:{of} \\ $$$${squared}\:{devition}. \\ $$
Commented by tawa tawa last updated on 31/May/17
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{Longest}\:\mathrm{time}\:\mathrm{sir}. \\ $$
