Question Number 14384 by ajfour last updated on 31/May/17

Commented by ajfour last updated on 31/May/17
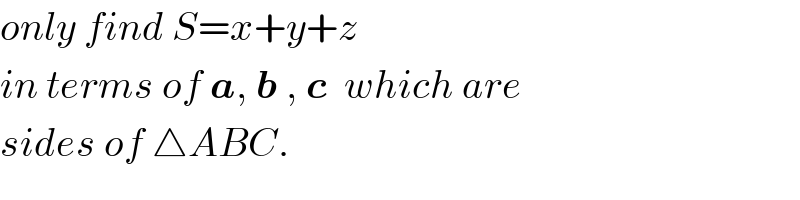
$${only}\:{find}\:{S}={x}+{y}+{z} \\ $$$${in}\:{terms}\:{of}\:\boldsymbol{{a}},\:\boldsymbol{{b}}\:,\:\boldsymbol{{c}}\:\:{which}\:{are} \\ $$$${sides}\:{of}\:\bigtriangleup{ABC}. \\ $$
Commented by RasheedSindhi last updated on 31/May/17

$$\mathrm{This}\:\mathrm{Question}\:\mathrm{is}\:\mathrm{closely}\:\mathrm{related} \\ $$$$\mathrm{to}\:\mathrm{Q}#\mathrm{14157}. \\ $$$$\mathrm{Same}\:\mathrm{equations}\:\mathrm{exist}\:\mathrm{here}! \\ $$
Commented by ajfour last updated on 31/May/17

$${yes},\:{i}\:{am}\:{searching}\:{for}\:{rather} \\ $$$${simple}\:{expeessions}\:{of}\:{x},{y},\:{and} \\ $$$${z}\:{in}\:{terms}\:{of}\:\boldsymbol{{a}},\:\boldsymbol{{b}},\:{and}\:\boldsymbol{{c}}\:. \\ $$$${outermost}\:\:{boundary}\:{of}\:{figure} \\ $$$${is}\:{a}\:{hexagon}\:{of}\:{side}\:{lengths} \\ $$$$\boldsymbol{{a}},\boldsymbol{{b}},\boldsymbol{{c}},\boldsymbol{{a}},\boldsymbol{{b}},\boldsymbol{{c}}\:\:\:{and}\:{in}\:{the}\:{same} \\ $$$${order}. \\ $$
Commented by RasheedSindhi last updated on 31/May/17

$$\angle\mathrm{CA}'\mathrm{B}=\mathrm{120}° \\ $$$$\mathrm{According}\:\mathrm{to}\:\mathrm{cosine}\:\mathrm{law} \\ $$$$\mathrm{a}^{\mathrm{2}} =\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} −\mathrm{2xy}\:\mathrm{cos}\:\angle\mathrm{CA}'\mathrm{B} \\ $$$$\mathrm{a}^{\mathrm{2}} =\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} −\mathrm{2xy}\:\mathrm{cos}\:\mathrm{120} \\ $$$$\mathrm{a}^{\mathrm{2}} =\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} −\mathrm{2xy}\left(−\mathrm{1}/\mathrm{2}\right) \\ $$$$\mathrm{a}^{\mathrm{2}} =\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} +\mathrm{xy} \\ $$$$\mathrm{In}\:\mathrm{a}\:\mathrm{similar}\:\mathrm{manner}\:\mathrm{the}\:\mathrm{remaining} \\ $$$$\mathrm{two}\:\mathrm{equtions}\:\mathrm{can}\:\mathrm{be}\:\mathrm{obtained}. \\ $$
Commented by mrW1 last updated on 31/May/17

$${very}\:{interesting}\:{try}! \\ $$$${geometric}\:{solutions}\:{are}\:{the}\:{most} \\ $$$${beautiful}\:{solutions},\:{because}\:{you} \\ $$$${can}\:{see}\:{and}\:{feel}\:{them}. \\ $$
Commented by RasheedSindhi last updated on 31/May/17

$$\mathcal{N}{ice}\:{Say}\:{Sir}! \\ $$
