Question-144085

Question Number 144085 by mohammad17 last updated on 21/Jun/21

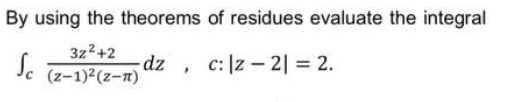
Commented by mohammad17 last updated on 21/Jun/21

$${help}\:{me}\:{sir} \\ $$

Answered by mathmax by abdo last updated on 21/Jun/21

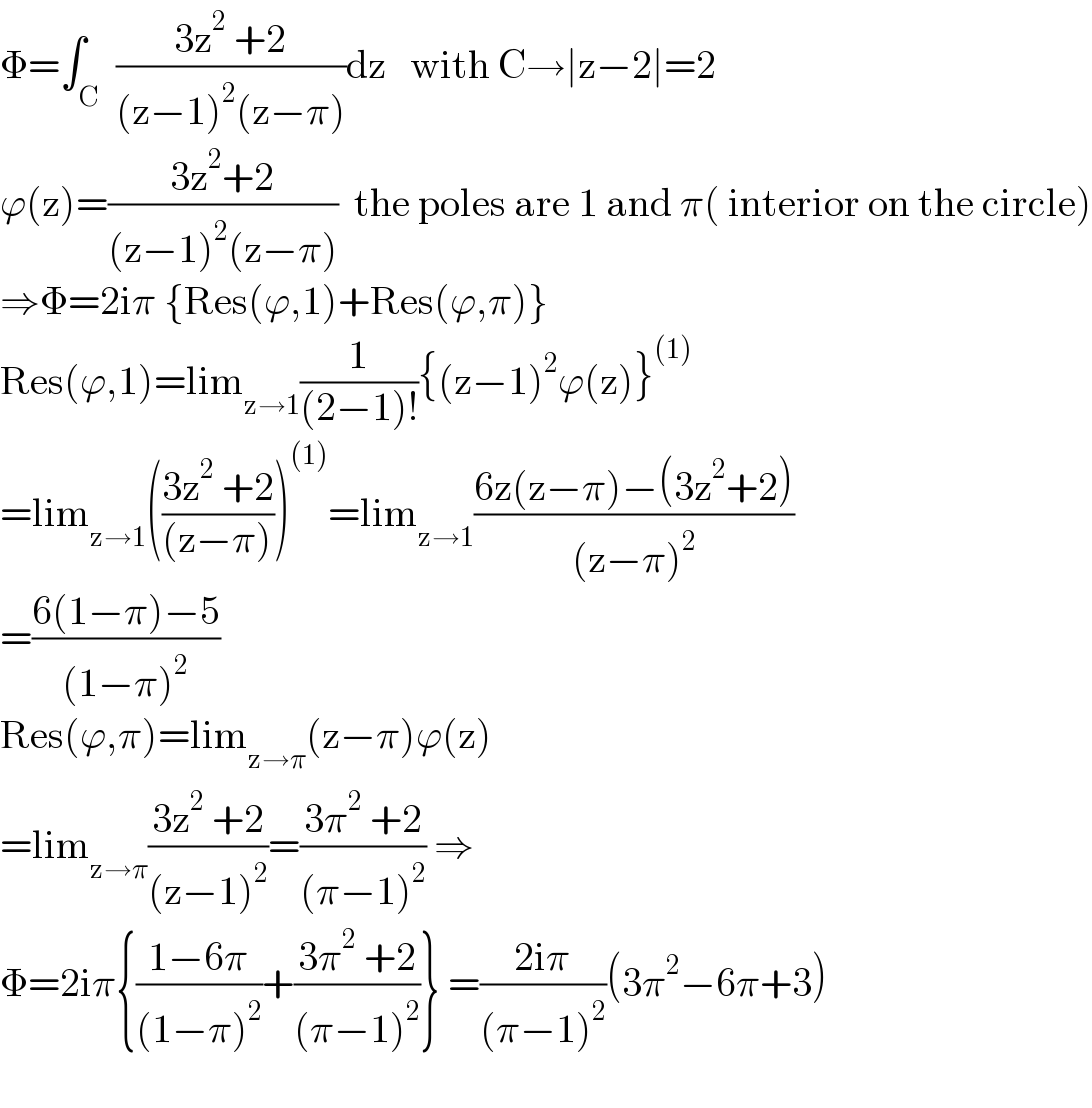
Φ=∫_C ((3z^2 +2)/((z−1)^2 (z−π)))dz with C→∣z−2∣=2 ϕ(z)=((3z^2 +2)/((z−1)^2 (z−π))) the poles are 1 and π( interior on the circle) ⇒Φ=2iπ {Res(ϕ,1)+Res(ϕ,π)} Res(ϕ,1)=lim_(z→1) (1/((2−1)!)){(z−1)^2 ϕ(z)}^((1)) =lim_(z→1) (((3z^2 +2)/((z−π))))^((1)) =lim_(z→1) ((6z(z−π)−(3z^2 +2))/((z−π)^2 )) =((6(1−π)−5)/((1−π)^2 )) Res(ϕ,π)=lim_(z→π) (z−π)ϕ(z) =lim_(z→π) ((3z^2 +2)/((z−1)^2 ))=((3π^2 +2)/((π−1)^2 )) ⇒ Φ=2iπ{((1−6π)/((1−π)^2 ))+((3π^2 +2)/((π−1)^2 ))} =((2iπ)/((π−1)^2 ))(3π^2 −6π+3)

$$\Phi=\int_{\mathrm{C}} \:\frac{\mathrm{3z}^{\mathrm{2}} \:+\mathrm{2}}{\left(\mathrm{z}−\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{z}−\pi\right)}\mathrm{dz}\:\:\:\mathrm{with}\:\mathrm{C}\rightarrow\mid\mathrm{z}−\mathrm{2}\mid=\mathrm{2} \\ $$$$\varphi\left(\mathrm{z}\right)=\frac{\mathrm{3z}^{\mathrm{2}} +\mathrm{2}}{\left(\mathrm{z}−\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{z}−\pi\right)}\:\:\mathrm{the}\:\mathrm{poles}\:\mathrm{are}\:\mathrm{1}\:\mathrm{and}\:\pi\left(\:\mathrm{interior}\:\mathrm{on}\:\mathrm{the}\:\mathrm{circle}\right) \\ $$$$\Rightarrow\Phi=\mathrm{2i}\pi\:\left\{\mathrm{Res}\left(\varphi,\mathrm{1}\right)+\mathrm{Res}\left(\varphi,\pi\right)\right\} \\ $$$$\mathrm{Res}\left(\varphi,\mathrm{1}\right)=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{1}} \frac{\mathrm{1}}{\left(\mathrm{2}−\mathrm{1}\right)!}\left\{\left(\mathrm{z}−\mathrm{1}\right)^{\mathrm{2}} \varphi\left(\mathrm{z}\right)\right\}^{\left(\mathrm{1}\right)} \\ $$$$=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{1}} \left(\frac{\mathrm{3z}^{\mathrm{2}} \:+\mathrm{2}}{\left(\mathrm{z}−\pi\right)}\right)^{\left(\mathrm{1}\right)} =\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{1}} \frac{\mathrm{6z}\left(\mathrm{z}−\pi\right)−\left(\mathrm{3z}^{\mathrm{2}} +\mathrm{2}\right)}{\left(\mathrm{z}−\pi\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{6}\left(\mathrm{1}−\pi\right)−\mathrm{5}}{\left(\mathrm{1}−\pi\right)^{\mathrm{2}} } \\ $$$$\mathrm{Res}\left(\varphi,\pi\right)=\mathrm{lim}_{\mathrm{z}\rightarrow\pi} \left(\mathrm{z}−\pi\right)\varphi\left(\mathrm{z}\right) \\ $$$$=\mathrm{lim}_{\mathrm{z}\rightarrow\pi} \frac{\mathrm{3z}^{\mathrm{2}} \:+\mathrm{2}}{\left(\mathrm{z}−\mathrm{1}\right)^{\mathrm{2}} }=\frac{\mathrm{3}\pi^{\mathrm{2}} \:+\mathrm{2}}{\left(\pi−\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\Phi=\mathrm{2i}\pi\left\{\frac{\mathrm{1}−\mathrm{6}\pi}{\left(\mathrm{1}−\pi\right)^{\mathrm{2}} }+\frac{\mathrm{3}\pi^{\mathrm{2}} \:+\mathrm{2}}{\left(\pi−\mathrm{1}\right)^{\mathrm{2}} }\right\}\:=\frac{\mathrm{2i}\pi}{\left(\pi−\mathrm{1}\right)^{\mathrm{2}} }\left(\mathrm{3}\pi^{\mathrm{2}} −\mathrm{6}\pi+\mathrm{3}\right) \\ $$$$ \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply