Question Number 144168 by bekzodjumayev last updated on 22/Jun/21

Answered by Olaf_Thorendsen last updated on 22/Jun/21
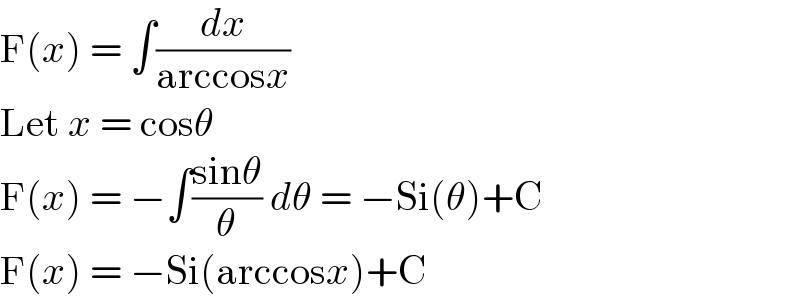
$$\mathrm{F}\left({x}\right)\:=\:\int\frac{{dx}}{\mathrm{arccos}{x}} \\ $$$$\mathrm{Let}\:{x}\:=\:\mathrm{cos}\theta \\ $$$$\mathrm{F}\left({x}\right)\:=\:−\int\frac{\mathrm{sin}\theta}{\theta}\:{d}\theta\:=\:−\mathrm{Si}\left(\theta\right)+\mathrm{C} \\ $$$$\mathrm{F}\left({x}\right)\:=\:−\mathrm{Si}\left(\mathrm{arccos}{x}\right)+\mathrm{C} \\ $$
Commented by bekzodjumayev last updated on 22/Jun/21

$${Thank}\:{you} \\ $$
