Menu Close

Question-144170

Tinku Tara 0 Comments
Pin




Question Number 144170 by mathdanisur last updated on 22/Jun/21
Answered by Olaf_Thorendsen last updated on 22/Jun/21
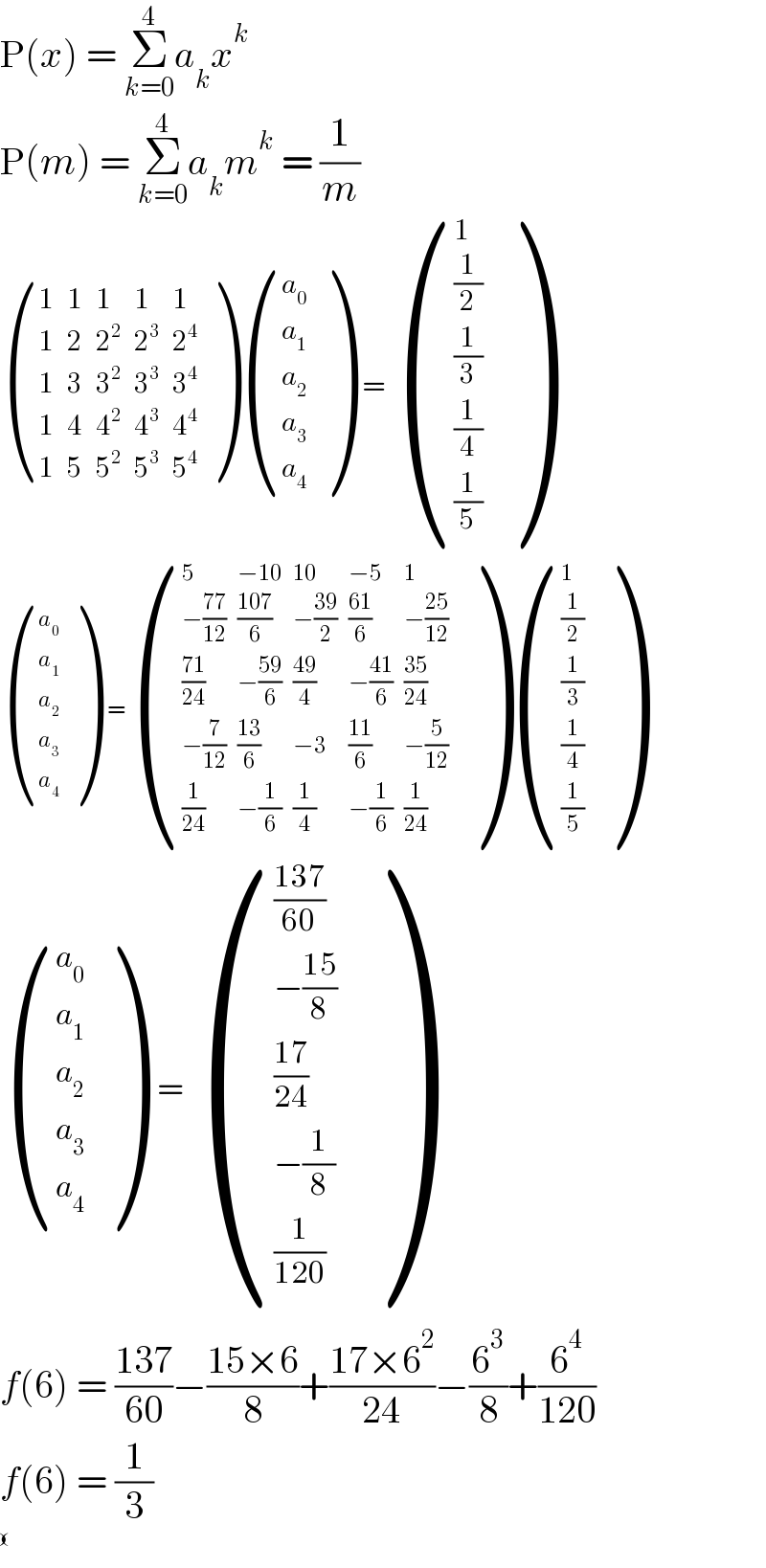
P(x) = Σ_(k=0) ^4 a_k x^k P(m) = Σ_(k=0) ^4 a_k m^k = (1/m) ((1,1,1,1,1),(1,2,2^2 ,2^3 ,2^4 ),(1,3,3^2 ,3^3 ,3^4 ),(1,4,4^2 ,4^3 ,4^4 ),(1,5,5^2 ,5^3 ,5^4 ) ) ((a_0 ),(a_1 ),(a_2 ),(a_3 ),(a_4 ) ) = ((1),((1/2)),((1/3)),((1/4)),((1/5)) ) ((a_0 ),(a_1 ),(a_2 ),(a_3 ),(a_4 ) ) = ((5,(−10),(10),(−5),1),((−((77)/(12))),((107)/6),(−((39)/2)),((61)/6),(−((25)/(12)))),(((71)/(24)),(−((59)/6)),((49)/4),(−((41)/6)),((35)/(24))),((−(7/(12))),((13)/6),(−3),((11)/6),(−(5/(12)))),((1/(24)),(−(1/6)),(1/4),(−(1/6)),(1/(24))) ) ((1),((1/2)),((1/3)),((1/4)),((1/5)) ) ((a_0 ),(a_1 ),(a_2 ),(a_3 ),(a_4 ) ) = ((((137)/(60))),((−((15)/8))),(((17)/(24))),((−(1/8))),((1/(120))) ) f(6) = ((137)/(60))−((15×6)/8)+((17×6^2 )/(24))−(6^3 /8)+(6^4 /(120)) f(6) = (1/3) ((),() )
$$\mathrm{P}\left({x}\right)\:=\:\underset{{k}=\mathrm{0}} {\overset{\mathrm{4}} {\sum}}{a}_{{k}} {x}^{{k}} \\ $$$$\mathrm{P}\left({m}\right)\:=\:\underset{{k}=\mathrm{0}} {\overset{\mathrm{4}} {\sum}}{a}_{{k}} {m}^{{k}} \:=\:\frac{\mathrm{1}}{{m}} \\ $$$$\begin{pmatrix}{\mathrm{1}}&{\mathrm{1}}&{\mathrm{1}}&{\mathrm{1}}&{\mathrm{1}}\\{\mathrm{1}}&{\mathrm{2}}&{\mathrm{2}^{\mathrm{2}} }&{\mathrm{2}^{\mathrm{3}} }&{\mathrm{2}^{\mathrm{4}} }\\{\mathrm{1}}&{\mathrm{3}}&{\mathrm{3}^{\mathrm{2}} }&{\mathrm{3}^{\mathrm{3}} }&{\mathrm{3}^{\mathrm{4}} }\\{\mathrm{1}}&{\mathrm{4}}&{\mathrm{4}^{\mathrm{2}} }&{\mathrm{4}^{\mathrm{3}} }&{\mathrm{4}^{\mathrm{4}} }\\{\mathrm{1}}&{\mathrm{5}}&{\mathrm{5}^{\mathrm{2}} }&{\mathrm{5}^{\mathrm{3}} }&{\mathrm{5}^{\mathrm{4}} }\end{pmatrix}\begin{pmatrix}{{a}_{\mathrm{0}} }\\{{a}_{\mathrm{1}} }\\{{a}_{\mathrm{2}} }\\{{a}_{\mathrm{3}} }\\{{a}_{\mathrm{4}} }\end{pmatrix}\:\:=\:\begin{pmatrix}{\mathrm{1}}\\{\frac{\mathrm{1}}{\mathrm{2}}}\\{\frac{\mathrm{1}}{\mathrm{3}}}\\{\frac{\mathrm{1}}{\mathrm{4}}}\\{\frac{\mathrm{1}}{\mathrm{5}}}\end{pmatrix} \\ $$$$\begin{pmatrix}{{a}_{\mathrm{0}} }\\{{a}_{\mathrm{1}} }\\{{a}_{\mathrm{2}} }\\{{a}_{\mathrm{3}} }\\{{a}_{\mathrm{4}} }\end{pmatrix}\:\:=\begin{pmatrix}{\mathrm{5}}&{−\mathrm{10}}&{\mathrm{10}}&{−\mathrm{5}}&{\mathrm{1}}\\{−\frac{\mathrm{77}}{\mathrm{12}}}&{\frac{\mathrm{107}}{\mathrm{6}}}&{−\frac{\mathrm{39}}{\mathrm{2}}}&{\frac{\mathrm{61}}{\mathrm{6}}}&{−\frac{\mathrm{25}}{\mathrm{12}}}\\{\frac{\mathrm{71}}{\mathrm{24}}}&{−\frac{\mathrm{59}}{\mathrm{6}}}&{\frac{\mathrm{49}}{\mathrm{4}}}&{−\frac{\mathrm{41}}{\mathrm{6}}}&{\frac{\mathrm{35}}{\mathrm{24}}}\\{−\frac{\mathrm{7}}{\mathrm{12}}}&{\frac{\mathrm{13}}{\mathrm{6}}}&{−\mathrm{3}}&{\frac{\mathrm{11}}{\mathrm{6}}}&{−\frac{\mathrm{5}}{\mathrm{12}}}\\{\frac{\mathrm{1}}{\mathrm{24}}}&{−\frac{\mathrm{1}}{\mathrm{6}}}&{\frac{\mathrm{1}}{\mathrm{4}}}&{−\frac{\mathrm{1}}{\mathrm{6}}}&{\frac{\mathrm{1}}{\mathrm{24}}}\end{pmatrix}\begin{pmatrix}{\mathrm{1}}\\{\frac{\mathrm{1}}{\mathrm{2}}}\\{\frac{\mathrm{1}}{\mathrm{3}}}\\{\frac{\mathrm{1}}{\mathrm{4}}}\\{\frac{\mathrm{1}}{\mathrm{5}}}\end{pmatrix}\:\: \\ $$$$\begin{pmatrix}{{a}_{\mathrm{0}} }\\{{a}_{\mathrm{1}} }\\{{a}_{\mathrm{2}} }\\{{a}_{\mathrm{3}} }\\{{a}_{\mathrm{4}} }\end{pmatrix}\:\:\:=\:\begin{pmatrix}{\frac{\mathrm{137}}{\mathrm{60}}}\\{−\frac{\mathrm{15}}{\mathrm{8}}}\\{\frac{\mathrm{17}}{\mathrm{24}}}\\{−\frac{\mathrm{1}}{\mathrm{8}}}\\{\frac{\mathrm{1}}{\mathrm{120}}}\end{pmatrix}\:\: \\ $$$${f}\left(\mathrm{6}\right)\:=\:\frac{\mathrm{137}}{\mathrm{60}}−\frac{\mathrm{15}×\mathrm{6}}{\mathrm{8}}+\frac{\mathrm{17}×\mathrm{6}^{\mathrm{2}} }{\mathrm{24}}−\frac{\mathrm{6}^{\mathrm{3}} }{\mathrm{8}}+\frac{\mathrm{6}^{\mathrm{4}} }{\mathrm{120}} \\ $$$${f}\left(\mathrm{6}\right)\:=\:\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\begin{pmatrix}\\\end{pmatrix} \\ $$
Commented by mathdanisur last updated on 22/Jun/21
alot perfect thank you Sir
$${alot}\:{perfect}\:{thank}\:{you}\:{Sir} \\ $$
Answered by mr W last updated on 22/Jun/21
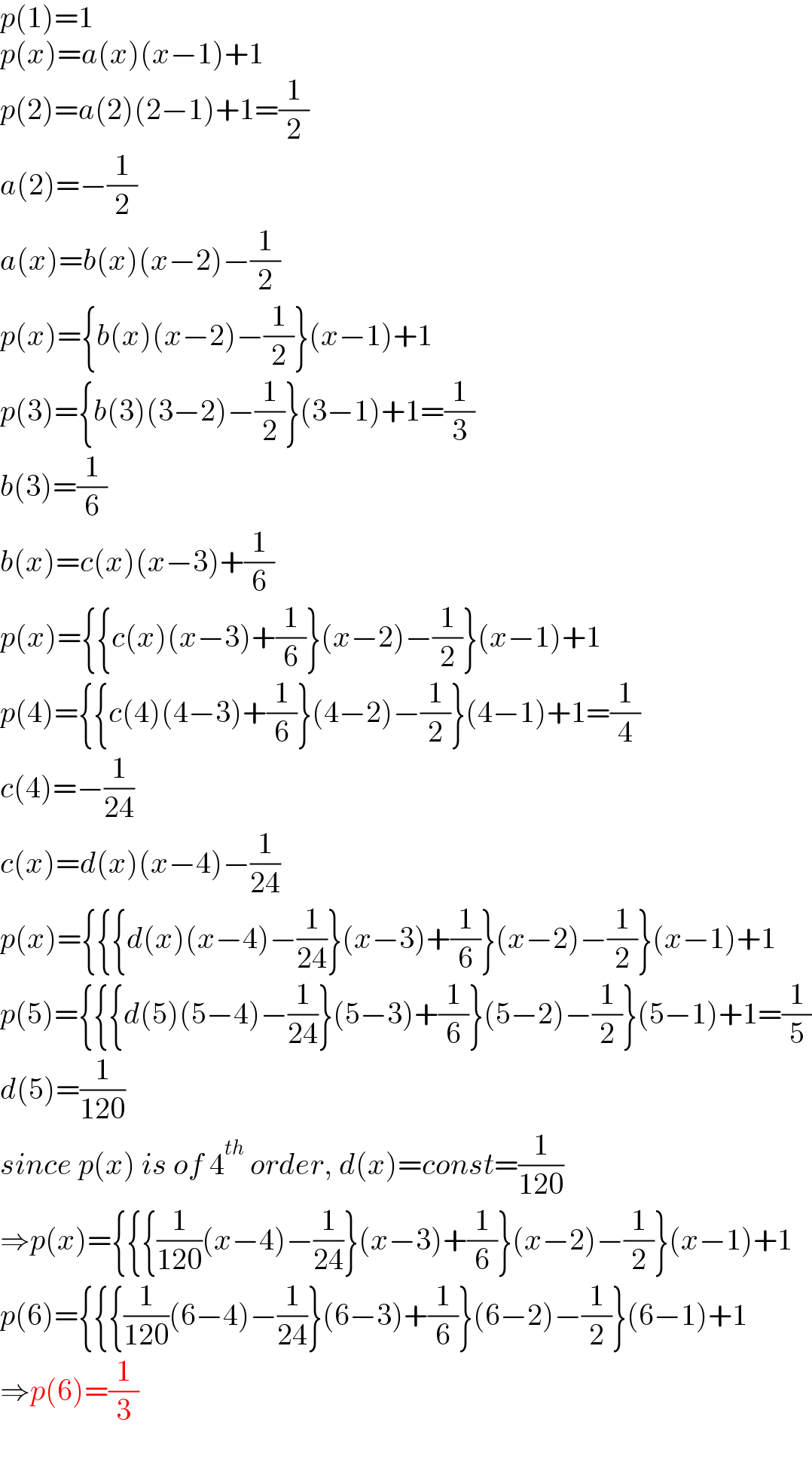
p(1)=1 p(x)=a(x)(x−1)+1 p(2)=a(2)(2−1)+1=(1/2) a(2)=−(1/2) a(x)=b(x)(x−2)−(1/2) p(x)={b(x)(x−2)−(1/2)}(x−1)+1 p(3)={b(3)(3−2)−(1/2)}(3−1)+1=(1/3) b(3)=(1/6) b(x)=c(x)(x−3)+(1/6) p(x)={{c(x)(x−3)+(1/6)}(x−2)−(1/2)}(x−1)+1 p(4)={{c(4)(4−3)+(1/6)}(4−2)−(1/2)}(4−1)+1=(1/4) c(4)=−(1/(24)) c(x)=d(x)(x−4)−(1/(24)) p(x)={{{d(x)(x−4)−(1/(24))}(x−3)+(1/6)}(x−2)−(1/2)}(x−1)+1 p(5)={{{d(5)(5−4)−(1/(24))}(5−3)+(1/6)}(5−2)−(1/2)}(5−1)+1=(1/5) d(5)=(1/(120)) since p(x) is of 4^(th) order, d(x)=const=(1/(120)) ⇒p(x)={{{(1/(120))(x−4)−(1/(24))}(x−3)+(1/6)}(x−2)−(1/2)}(x−1)+1 p(6)={{{(1/(120))(6−4)−(1/(24))}(6−3)+(1/6)}(6−2)−(1/2)}(6−1)+1 ⇒p(6)=(1/3)
$${p}\left(\mathrm{1}\right)=\mathrm{1} \\ $$$${p}\left({x}\right)={a}\left({x}\right)\left({x}−\mathrm{1}\right)+\mathrm{1} \\ $$$${p}\left(\mathrm{2}\right)={a}\left(\mathrm{2}\right)\left(\mathrm{2}−\mathrm{1}\right)+\mathrm{1}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${a}\left(\mathrm{2}\right)=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${a}\left({x}\right)={b}\left({x}\right)\left({x}−\mathrm{2}\right)−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${p}\left({x}\right)=\left\{{b}\left({x}\right)\left({x}−\mathrm{2}\right)−\frac{\mathrm{1}}{\mathrm{2}}\right\}\left({x}−\mathrm{1}\right)+\mathrm{1} \\ $$$${p}\left(\mathrm{3}\right)=\left\{{b}\left(\mathrm{3}\right)\left(\mathrm{3}−\mathrm{2}\right)−\frac{\mathrm{1}}{\mathrm{2}}\right\}\left(\mathrm{3}−\mathrm{1}\right)+\mathrm{1}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${b}\left(\mathrm{3}\right)=\frac{\mathrm{1}}{\mathrm{6}} \\ $$$${b}\left({x}\right)={c}\left({x}\right)\left({x}−\mathrm{3}\right)+\frac{\mathrm{1}}{\mathrm{6}} \\ $$$${p}\left({x}\right)=\left\{\left\{{c}\left({x}\right)\left({x}−\mathrm{3}\right)+\frac{\mathrm{1}}{\mathrm{6}}\right\}\left({x}−\mathrm{2}\right)−\frac{\mathrm{1}}{\mathrm{2}}\right\}\left({x}−\mathrm{1}\right)+\mathrm{1} \\ $$$${p}\left(\mathrm{4}\right)=\left\{\left\{{c}\left(\mathrm{4}\right)\left(\mathrm{4}−\mathrm{3}\right)+\frac{\mathrm{1}}{\mathrm{6}}\right\}\left(\mathrm{4}−\mathrm{2}\right)−\frac{\mathrm{1}}{\mathrm{2}}\right\}\left(\mathrm{4}−\mathrm{1}\right)+\mathrm{1}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${c}\left(\mathrm{4}\right)=−\frac{\mathrm{1}}{\mathrm{24}} \\ $$$${c}\left({x}\right)={d}\left({x}\right)\left({x}−\mathrm{4}\right)−\frac{\mathrm{1}}{\mathrm{24}} \\ $$$${p}\left({x}\right)=\left\{\left\{\left\{{d}\left({x}\right)\left({x}−\mathrm{4}\right)−\frac{\mathrm{1}}{\mathrm{24}}\right\}\left({x}−\mathrm{3}\right)+\frac{\mathrm{1}}{\mathrm{6}}\right\}\left({x}−\mathrm{2}\right)−\frac{\mathrm{1}}{\mathrm{2}}\right\}\left({x}−\mathrm{1}\right)+\mathrm{1} \\ $$$${p}\left(\mathrm{5}\right)=\left\{\left\{\left\{{d}\left(\mathrm{5}\right)\left(\mathrm{5}−\mathrm{4}\right)−\frac{\mathrm{1}}{\mathrm{24}}\right\}\left(\mathrm{5}−\mathrm{3}\right)+\frac{\mathrm{1}}{\mathrm{6}}\right\}\left(\mathrm{5}−\mathrm{2}\right)−\frac{\mathrm{1}}{\mathrm{2}}\right\}\left(\mathrm{5}−\mathrm{1}\right)+\mathrm{1}=\frac{\mathrm{1}}{\mathrm{5}} \\ $$$${d}\left(\mathrm{5}\right)=\frac{\mathrm{1}}{\mathrm{120}} \\ $$$${since}\:{p}\left({x}\right)\:{is}\:{of}\:\mathrm{4}^{{th}} \:{order},\:{d}\left({x}\right)={const}=\frac{\mathrm{1}}{\mathrm{120}} \\ $$$$\Rightarrow{p}\left({x}\right)=\left\{\left\{\left\{\frac{\mathrm{1}}{\mathrm{120}}\left({x}−\mathrm{4}\right)−\frac{\mathrm{1}}{\mathrm{24}}\right\}\left({x}−\mathrm{3}\right)+\frac{\mathrm{1}}{\mathrm{6}}\right\}\left({x}−\mathrm{2}\right)−\frac{\mathrm{1}}{\mathrm{2}}\right\}\left({x}−\mathrm{1}\right)+\mathrm{1} \\ $$$${p}\left(\mathrm{6}\right)=\left\{\left\{\left\{\frac{\mathrm{1}}{\mathrm{120}}\left(\mathrm{6}−\mathrm{4}\right)−\frac{\mathrm{1}}{\mathrm{24}}\right\}\left(\mathrm{6}−\mathrm{3}\right)+\frac{\mathrm{1}}{\mathrm{6}}\right\}\left(\mathrm{6}−\mathrm{2}\right)−\frac{\mathrm{1}}{\mathrm{2}}\right\}\left(\mathrm{6}−\mathrm{1}\right)+\mathrm{1} \\ $$$$\Rightarrow{p}\left(\mathrm{6}\right)=\frac{\mathrm{1}}{\mathrm{3}} \\ $$
Commented by mathdanisur last updated on 22/Jun/21
alot perfect thanks Sir
$${alot}\:{perfect}\:{thanks}\:{Sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *