Question-144237

Question Number 144237 by mathdanisur last updated on 23/Jun/21

Answered by MJS_new last updated on 23/Jun/21

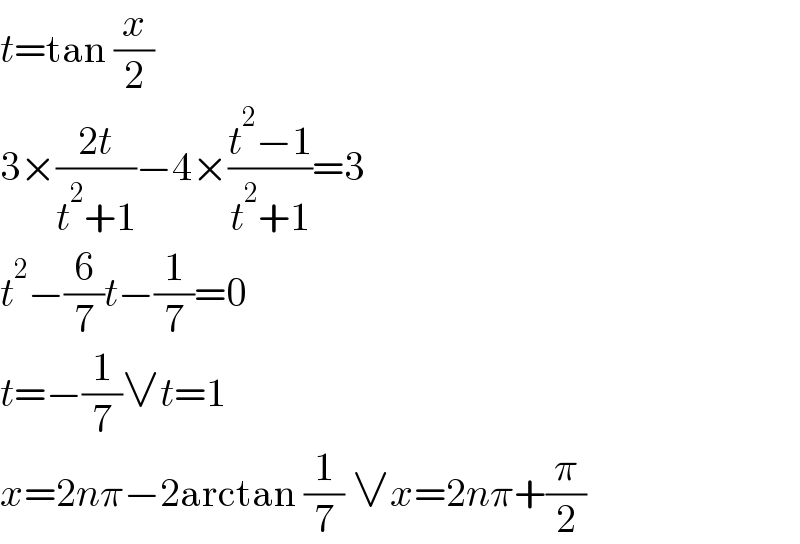
t=tan (x/2) 3×((2t)/(t^2 +1))−4×((t^2 −1)/(t^2 +1))=3 t^2 −(6/7)t−(1/7)=0 t=−(1/7)∨t=1 x=2nπ−2arctan (1/7) ∨x=2nπ+(π/2)

$${t}=\mathrm{tan}\:\frac{{x}}{\mathrm{2}} \\ $$$$\mathrm{3}×\frac{\mathrm{2}{t}}{{t}^{\mathrm{2}} +\mathrm{1}}−\mathrm{4}×\frac{{t}^{\mathrm{2}} −\mathrm{1}}{{t}^{\mathrm{2}} +\mathrm{1}}=\mathrm{3} \\ $$$${t}^{\mathrm{2}} −\frac{\mathrm{6}}{\mathrm{7}}{t}−\frac{\mathrm{1}}{\mathrm{7}}=\mathrm{0} \\ $$$${t}=−\frac{\mathrm{1}}{\mathrm{7}}\vee{t}=\mathrm{1} \\ $$$${x}=\mathrm{2}{n}\pi−\mathrm{2arctan}\:\frac{\mathrm{1}}{\mathrm{7}}\:\vee{x}=\mathrm{2}{n}\pi+\frac{\pi}{\mathrm{2}} \\ $$

Commented by mathdanisur last updated on 23/Jun/21

$${Thank}\:{you}\:{Sir} \\ $$

Answered by mathmax by abdo last updated on 23/Jun/21

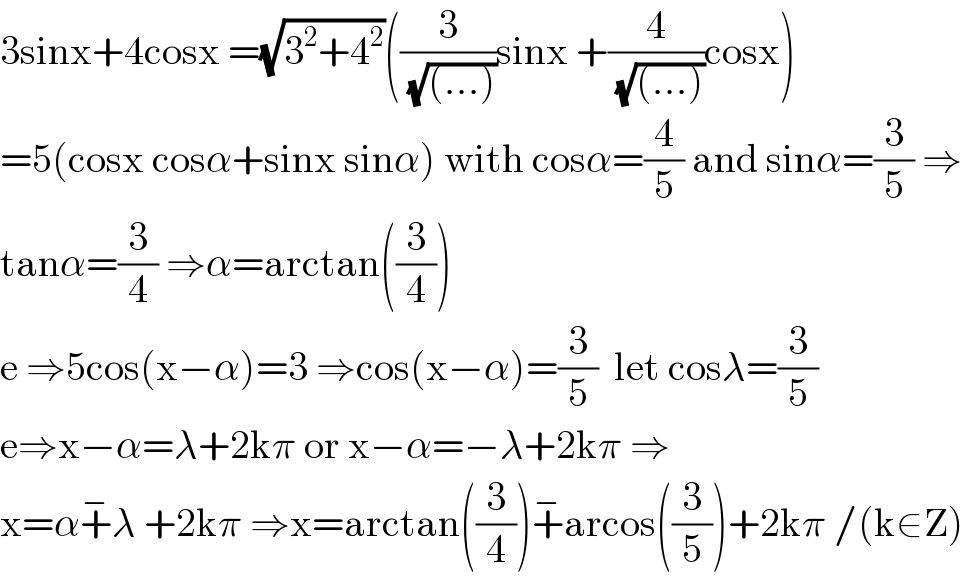
3sinx+4cosx =(√(3^2 +4^2 ))((3/( (√((...)))))sinx +(4/( (√((...)))))cosx) =5(cosx cosα+sinx sinα) with cosα=(4/5) and sinα=(3/5) ⇒ tanα=(3/4) ⇒α=arctan((3/4)) e ⇒5cos(x−α)=3 ⇒cos(x−α)=(3/5) let cosλ=(3/5) e⇒x−α=λ+2kπ or x−α=−λ+2kπ ⇒ x=α+^− λ +2kπ ⇒x=arctan((3/4))+^− arcos((3/5))+2kπ /(k∈Z)

$$\mathrm{3sinx}+\mathrm{4cosx}\:=\sqrt{\mathrm{3}^{\mathrm{2}} +\mathrm{4}^{\mathrm{2}} }\left(\frac{\mathrm{3}}{\:\sqrt{\left(…\right)}}\mathrm{sinx}\:+\frac{\mathrm{4}}{\:\sqrt{\left(…\right)}}\mathrm{cosx}\right) \\ $$$$=\mathrm{5}\left(\mathrm{cosx}\:\mathrm{cos}\alpha+\mathrm{sinx}\:\mathrm{sin}\alpha\right)\:\mathrm{with}\:\mathrm{cos}\alpha=\frac{\mathrm{4}}{\mathrm{5}}\:\mathrm{and}\:\mathrm{sin}\alpha=\frac{\mathrm{3}}{\mathrm{5}}\:\Rightarrow \\ $$$$\mathrm{tan}\alpha=\frac{\mathrm{3}}{\mathrm{4}}\:\Rightarrow\alpha=\mathrm{arctan}\left(\frac{\mathrm{3}}{\mathrm{4}}\right) \\ $$$$\mathrm{e}\:\Rightarrow\mathrm{5cos}\left(\mathrm{x}−\alpha\right)=\mathrm{3}\:\Rightarrow\mathrm{cos}\left(\mathrm{x}−\alpha\right)=\frac{\mathrm{3}}{\mathrm{5}}\:\:\mathrm{let}\:\mathrm{cos}\lambda=\frac{\mathrm{3}}{\mathrm{5}} \\ $$$$\mathrm{e}\Rightarrow\mathrm{x}−\alpha=\lambda+\mathrm{2k}\pi\:\mathrm{or}\:\mathrm{x}−\alpha=−\lambda+\mathrm{2k}\pi\:\Rightarrow \\ $$$$\mathrm{x}=\alpha\overset{−} {+}\lambda\:+\mathrm{2k}\pi\:\Rightarrow\mathrm{x}=\mathrm{arctan}\left(\frac{\mathrm{3}}{\mathrm{4}}\right)\overset{−} {+}\mathrm{arcos}\left(\frac{\mathrm{3}}{\mathrm{5}}\right)+\mathrm{2k}\pi\:/\left(\mathrm{k}\in\mathrm{Z}\right) \\ $$

Commented by mathdanisur last updated on 23/Jun/21

$${Thank}\:{you}\:{Sir} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply