Question Number 144248 by Pagnol last updated on 23/Jun/21

Answered by Ar Brandon last updated on 23/Jun/21
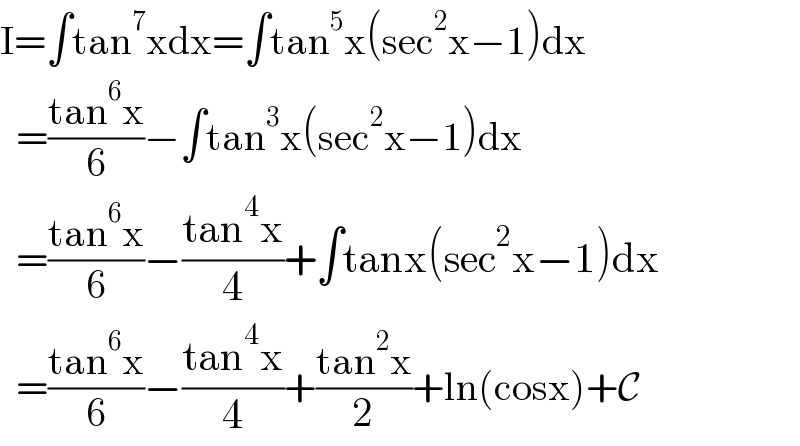
$$\mathrm{I}=\int\mathrm{tan}^{\mathrm{7}} \mathrm{xdx}=\int\mathrm{tan}^{\mathrm{5}} \mathrm{x}\left(\mathrm{sec}^{\mathrm{2}} \mathrm{x}−\mathrm{1}\right)\mathrm{dx} \\ $$$$\:\:=\frac{\mathrm{tan}^{\mathrm{6}} \mathrm{x}}{\mathrm{6}}−\int\mathrm{tan}^{\mathrm{3}} \mathrm{x}\left(\mathrm{sec}^{\mathrm{2}} \mathrm{x}−\mathrm{1}\right)\mathrm{dx} \\ $$$$\:\:=\frac{\mathrm{tan}^{\mathrm{6}} \mathrm{x}}{\mathrm{6}}−\frac{\mathrm{tan}^{\mathrm{4}} \mathrm{x}}{\mathrm{4}}+\int\mathrm{tanx}\left(\mathrm{sec}^{\mathrm{2}} \mathrm{x}−\mathrm{1}\right)\mathrm{dx} \\ $$$$\:\:=\frac{\mathrm{tan}^{\mathrm{6}} \mathrm{x}}{\mathrm{6}}−\frac{\mathrm{tan}^{\mathrm{4}} \mathrm{x}}{\mathrm{4}}+\frac{\mathrm{tan}^{\mathrm{2}} \mathrm{x}}{\mathrm{2}}+\mathrm{ln}\left(\mathrm{cosx}\right)+\mathcal{C} \\ $$
Commented by Ar Brandon last updated on 23/Jun/21

$$\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}=\mathrm{sec}^{\mathrm{2}} \mathrm{x} \\ $$$$\frac{\mathrm{d}\left(\mathrm{tanx}\right)}{\mathrm{dx}}=\mathrm{sec}^{\mathrm{2}} \mathrm{x} \\ $$
