Question Number 144268 by aliibrahim1 last updated on 23/Jun/21
Answered by imjagoll last updated on 24/Jun/21
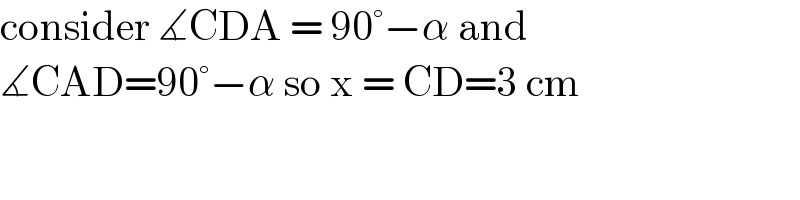
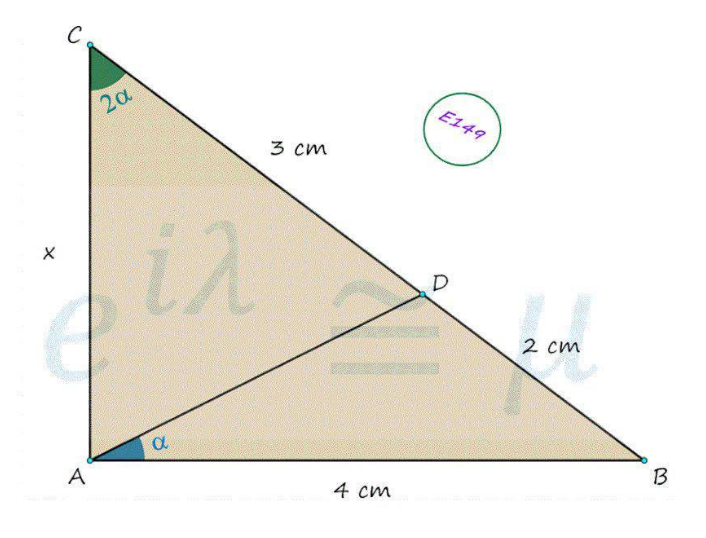
$$\mathrm{consider}\:\measuredangle\mathrm{CDA}\:=\:\mathrm{90}°−\alpha\:\mathrm{and}\: \\ $$$$\measuredangle\mathrm{CAD}=\mathrm{90}°−\alpha\:\mathrm{so}\:\mathrm{x}\:=\:\mathrm{CD}=\mathrm{3}\:\mathrm{cm} \\ $$
Commented by som(math1967) last updated on 24/Jun/21

$${Is}\:\measuredangle{BAC}=\mathrm{90}°\:?\: \\ $$
Answered by mr W last updated on 24/Jun/21
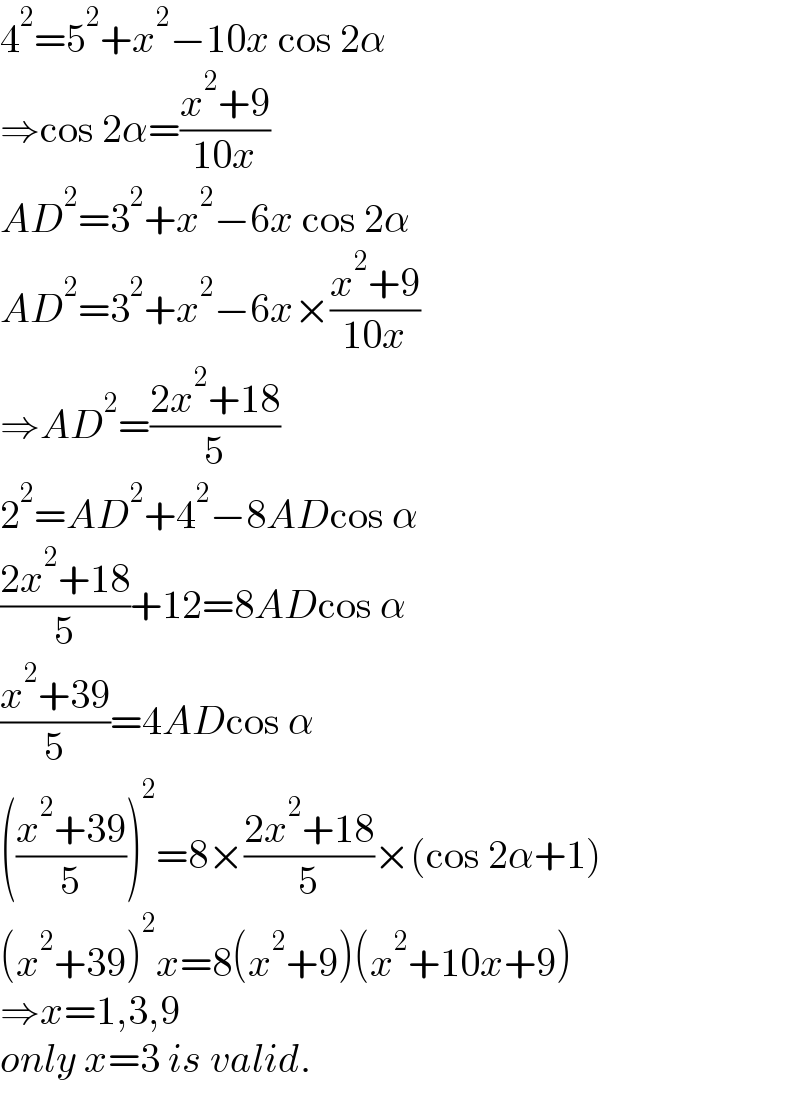
$$\mathrm{4}^{\mathrm{2}} =\mathrm{5}^{\mathrm{2}} +{x}^{\mathrm{2}} −\mathrm{10}{x}\:\mathrm{cos}\:\mathrm{2}\alpha \\ $$$$\Rightarrow\mathrm{cos}\:\mathrm{2}\alpha=\frac{{x}^{\mathrm{2}} +\mathrm{9}}{\mathrm{10}{x}} \\ $$$${AD}^{\mathrm{2}} =\mathrm{3}^{\mathrm{2}} +{x}^{\mathrm{2}} −\mathrm{6}{x}\:\mathrm{cos}\:\mathrm{2}\alpha \\ $$$${AD}^{\mathrm{2}} =\mathrm{3}^{\mathrm{2}} +{x}^{\mathrm{2}} −\mathrm{6}{x}×\frac{{x}^{\mathrm{2}} +\mathrm{9}}{\mathrm{10}{x}} \\ $$$$\Rightarrow{AD}^{\mathrm{2}} =\frac{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{18}}{\mathrm{5}} \\ $$$$\mathrm{2}^{\mathrm{2}} ={AD}^{\mathrm{2}} +\mathrm{4}^{\mathrm{2}} −\mathrm{8}{AD}\mathrm{cos}\:\alpha \\ $$$$\frac{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{18}}{\mathrm{5}}+\mathrm{12}=\mathrm{8}{AD}\mathrm{cos}\:\alpha \\ $$$$\frac{{x}^{\mathrm{2}} +\mathrm{39}}{\mathrm{5}}=\mathrm{4}{AD}\mathrm{cos}\:\alpha \\ $$$$\left(\frac{{x}^{\mathrm{2}} +\mathrm{39}}{\mathrm{5}}\right)^{\mathrm{2}} =\mathrm{8}×\frac{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{18}}{\mathrm{5}}×\left(\mathrm{cos}\:\mathrm{2}\alpha+\mathrm{1}\right) \\ $$$$\left({x}^{\mathrm{2}} +\mathrm{39}\right)^{\mathrm{2}} {x}=\mathrm{8}\left({x}^{\mathrm{2}} +\mathrm{9}\right)\left({x}^{\mathrm{2}} +\mathrm{10}{x}+\mathrm{9}\right) \\ $$$$\Rightarrow{x}=\mathrm{1},\mathrm{3},\mathrm{9} \\ $$$${only}\:{x}=\mathrm{3}\:{is}\:{valid}. \\ $$
