Question Number 14440 by christine last updated on 31/May/17
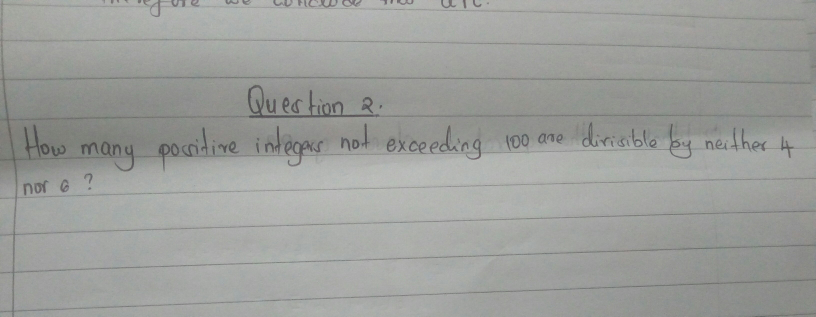
Answered by prakash jain last updated on 31/May/17

$$\mathrm{number}\:\mathrm{of}\:\mathrm{integer}\:\mathrm{1}\leqslant{n}\leqslant\mathrm{100} \\ $$$$\mathrm{divisible}\:\mathrm{by}\:\mathrm{4}\:=\lfloor\frac{\mathrm{100}}{\mathrm{4}}\rfloor=\mathrm{25} \\ $$$$\mathrm{divisible}\:\mathrm{by}\:\mathrm{6}\:=\lfloor\frac{\mathrm{100}}{\mathrm{6}}\rfloor=\mathrm{16} \\ $$$$\mathrm{divisible}\:\mathrm{by}\:\mathrm{by}\:\mathrm{4}\:\mathrm{and}\:\mathrm{6}\:=\lfloor\frac{\mathrm{100}}{\mathrm{12}}\rfloor=\mathrm{8} \\ $$$$\:\:\:\:\:\left(\mathrm{12}\:\mathrm{is}\:\mathrm{lcm}\:\mathrm{for}\:\mathrm{4}\:\mathrm{and}\:\mathrm{6}\right) \\ $$$$−−−−−− \\ $$$$\mathrm{number}\:\mathrm{of}\:\mathrm{integer}\:\mathrm{1}\leqslant{n}\leqslant\mathrm{100} \\ $$$$\mathrm{divisible}\:\mathrm{by}\:\mathrm{4}\:\mathrm{or}\:\mathrm{6}=\mathrm{25}+\mathrm{16}−\mathrm{8}=\mathrm{33} \\ $$$$ \\ $$$$\mathrm{number}\:\mathrm{of}\:\mathrm{integers}\:\mathrm{not}\:\mathrm{divisible} \\ $$$$\mathrm{by}\:\mathrm{4}\:\mathrm{or}\:\mathrm{6}=\mathrm{100}−\mathrm{33}=\mathrm{67} \\ $$
