Question Number 144439 by mathdanisur last updated on 25/Jun/21

Commented by Rasheed.Sindhi last updated on 25/Jun/21
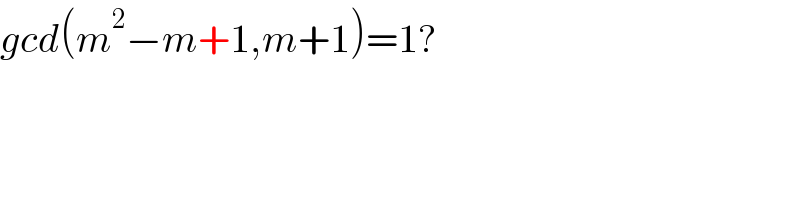
$${gcd}\left({m}^{\mathrm{2}} −{m}+\mathrm{1},{m}+\mathrm{1}\right)=\mathrm{1}? \\ $$
Commented by mathdanisur last updated on 25/Jun/21

$${sorry}\:{Sir},\:{yes}\:+\mathrm{1} \\ $$
Commented by mathmax by abdo last updated on 25/Jun/21
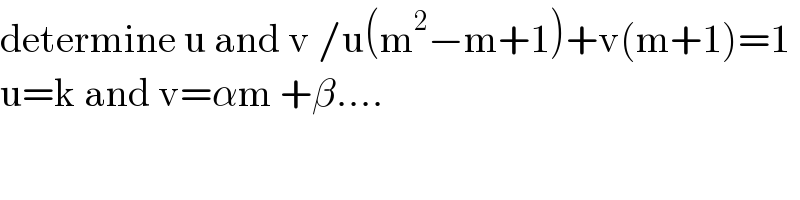
$$\mathrm{determine}\:\mathrm{u}\:\mathrm{and}\:\mathrm{v}\:/\mathrm{u}\left(\mathrm{m}^{\mathrm{2}} −\mathrm{m}+\mathrm{1}\right)+\mathrm{v}\left(\mathrm{m}+\mathrm{1}\right)=\mathrm{1} \\ $$$$\mathrm{u}=\mathrm{k}\:\mathrm{and}\:\mathrm{v}=\alpha\mathrm{m}\:+\beta…. \\ $$
Commented by Rasheed.Sindhi last updated on 26/Jun/21
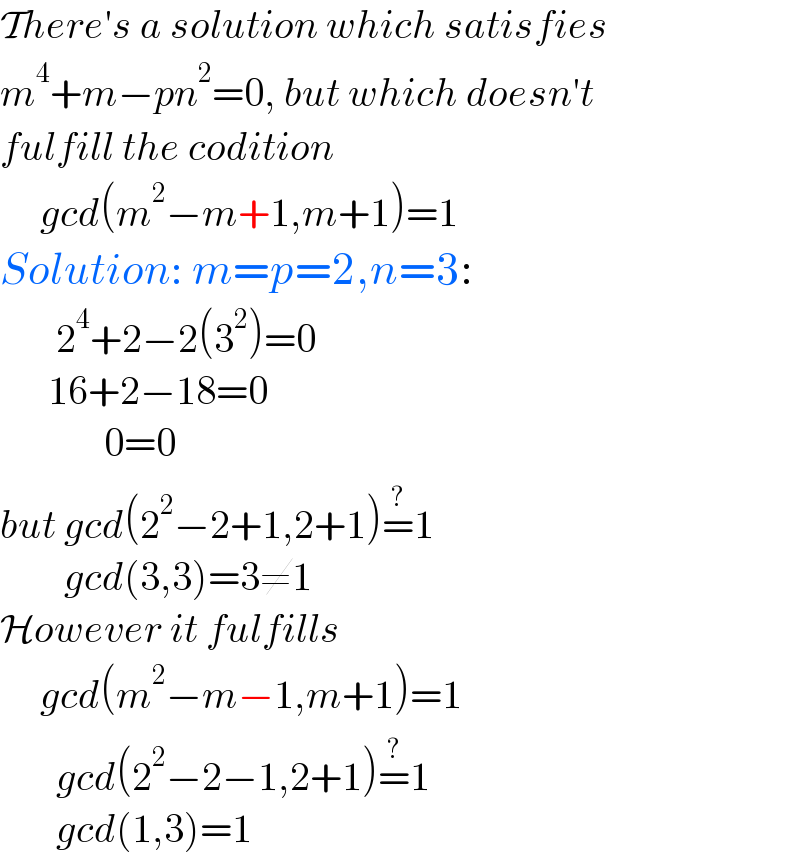
$$\mathcal{T}{here}'{s}\:{a}\:{solution}\:{which}\:{satisfies} \\ $$$${m}^{\mathrm{4}} +{m}−{pn}^{\mathrm{2}} =\mathrm{0},\:{but}\:{which}\:{doesn}'{t} \\ $$$${fulfill}\:{the}\:{codition} \\ $$$$\:\:\:\:\:{gcd}\left({m}^{\mathrm{2}} −{m}+\mathrm{1},{m}+\mathrm{1}\right)=\mathrm{1} \\ $$$${Solution}:\:{m}={p}=\mathrm{2},{n}=\mathrm{3}: \\ $$$$\:\:\:\:\:\:\:\mathrm{2}^{\mathrm{4}} +\mathrm{2}−\mathrm{2}\left(\mathrm{3}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\:\:\:\:\:\:\mathrm{16}+\mathrm{2}−\mathrm{18}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}=\mathrm{0} \\ $$$${but}\:{gcd}\left(\mathrm{2}^{\mathrm{2}} −\mathrm{2}+\mathrm{1},\mathrm{2}+\mathrm{1}\right)\overset{?} {=}\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:{gcd}\left(\mathrm{3},\mathrm{3}\right)=\mathrm{3}\neq\mathrm{1} \\ $$$$\mathcal{H}{owever}\:{it}\:{fulfills} \\ $$$$\:\:\:\:\:{gcd}\left({m}^{\mathrm{2}} −{m}−\mathrm{1},{m}+\mathrm{1}\right)=\mathrm{1} \\ $$$$\:\:\:\:\:\:\:{gcd}\left(\mathrm{2}^{\mathrm{2}} −\mathrm{2}−\mathrm{1},\mathrm{2}+\mathrm{1}\right)\overset{?} {=}\mathrm{1} \\ $$$$\:\:\:\:\:\:\:{gcd}\left(\mathrm{1},\mathrm{3}\right)=\mathrm{1} \\ $$
Answered by Rasheed.Sindhi last updated on 26/Jun/21
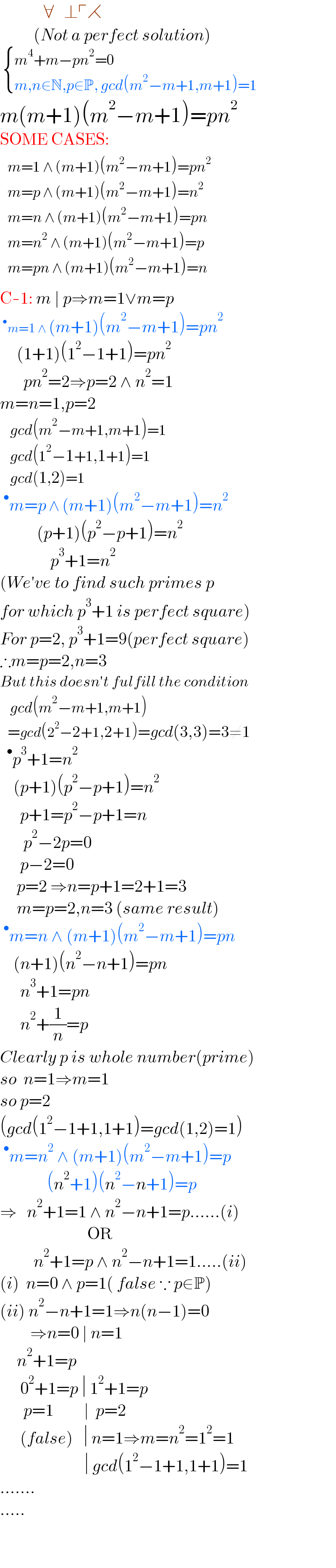
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\forall\:\:\:\bot\ulcorner\rightthreetimes \\ $$$$\:\:\:\:\:\:\:\:\:\:\left({Not}\:{a}\:{perfect}\:{solution}\right) \\ $$$$\:\begin{cases}{{m}^{\mathrm{4}} +{m}−{pn}^{\mathrm{2}} =\mathrm{0}}\\{{m},{n}\in\mathbb{N},{p}\in\mathbb{P},\:{gcd}\left({m}^{\mathrm{2}} −{m}+\mathrm{1},{m}+\mathrm{1}\right)=\mathrm{1}}\end{cases} \\ $$$${m}\left({m}+\mathrm{1}\right)\left({m}^{\mathrm{2}} −{m}+\mathrm{1}\right)={pn}^{\mathrm{2}} \\ $$$$\mathrm{SOME}\:\mathrm{CASES}: \\ $$$$\begin{matrix}{{m}=\mathrm{1}\:\wedge\:\left({m}+\mathrm{1}\right)\left({m}^{\mathrm{2}} −{m}+\mathrm{1}\right)={pn}^{\mathrm{2}} }\\{{m}={p}\:\wedge\:\left({m}+\mathrm{1}\right)\left({m}^{\mathrm{2}} −{m}+\mathrm{1}\right)={n}^{\mathrm{2}} }\\{{m}={n}\:\wedge\:\left({m}+\mathrm{1}\right)\left({m}^{\mathrm{2}} −{m}+\mathrm{1}\right)={pn}}\\{{m}={n}^{\mathrm{2}} \:\wedge\:\left({m}+\mathrm{1}\right)\left({m}^{\mathrm{2}} −{m}+\mathrm{1}\right)={p}}\\{{m}={pn}\:\wedge\:\left({m}+\mathrm{1}\right)\left({m}^{\mathrm{2}} −{m}+\mathrm{1}\right)={n}}\end{matrix} \\ $$$$\mathrm{C}-\mathrm{1}:\:{m}\:\mid\:{p}\Rightarrow{m}=\mathrm{1}\vee{m}={p} \\ $$$$\:^{\bullet} {m}=\mathrm{1}\:\wedge\:\left({m}+\mathrm{1}\right)\left({m}^{\mathrm{2}} −{m}+\mathrm{1}\right)={pn}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\left(\mathrm{1}+\mathrm{1}\right)\left(\mathrm{1}^{\mathrm{2}} −\mathrm{1}+\mathrm{1}\right)={pn}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:{pn}^{\mathrm{2}} =\mathrm{2}\Rightarrow{p}=\mathrm{2}\:\wedge\:{n}^{\mathrm{2}} =\mathrm{1} \\ $$$${m}={n}=\mathrm{1},{p}=\mathrm{2} \\ $$$$\:\:\:{gcd}\left({m}^{\mathrm{2}} −{m}+\mathrm{1},{m}+\mathrm{1}\right)=\mathrm{1} \\ $$$$\:\:\:{gcd}\left(\mathrm{1}^{\mathrm{2}} −\mathrm{1}+\mathrm{1},\mathrm{1}+\mathrm{1}\right)=\mathrm{1} \\ $$$$\:\:\:{gcd}\left(\mathrm{1},\mathrm{2}\right)=\mathrm{1} \\ $$$$\:^{\bullet} {m}={p}\:\wedge\:\left({m}+\mathrm{1}\right)\left({m}^{\mathrm{2}} −{m}+\mathrm{1}\right)={n}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\left({p}+\mathrm{1}\right)\left({p}^{\mathrm{2}} −{p}+\mathrm{1}\right)={n}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{p}^{\mathrm{3}} +\mathrm{1}={n}^{\mathrm{2}} \\ $$$$\left({We}'{ve}\:{to}\:{find}\:{such}\:{primes}\:{p}\right. \\ $$$$\left.{for}\:{which}\:{p}^{\mathrm{3}} +\mathrm{1}\:{is}\:{perfect}\:{square}\right) \\ $$$${For}\:{p}=\mathrm{2},\:{p}^{\mathrm{3}} +\mathrm{1}=\mathrm{9}\left({perfect}\:{square}\right) \\ $$$$\therefore{m}={p}=\mathrm{2},{n}=\mathrm{3} \\ $$$${But}\:{this}\:{doesn}'{t}\:{fulfill}\:{the}\:{condition} \\ $$$$\:\:\:{gcd}\left({m}^{\mathrm{2}} −{m}+\mathrm{1},{m}+\mathrm{1}\right) \\ $$$$\:\:\:={gcd}\left(\mathrm{2}^{\mathrm{2}} −\mathrm{2}+\mathrm{1},\mathrm{2}+\mathrm{1}\right)={gcd}\left(\mathrm{3},\mathrm{3}\right)=\mathrm{3}\neq\mathrm{1} \\ $$$$\:\:^{\bullet} {p}^{\mathrm{3}} +\mathrm{1}={n}^{\mathrm{2}} \\ $$$$\:\:\:\:\left({p}+\mathrm{1}\right)\left({p}^{\mathrm{2}} −{p}+\mathrm{1}\right)={n}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:{p}+\mathrm{1}={p}^{\mathrm{2}} −{p}+\mathrm{1}={n} \\ $$$$\:\:\:\:\:\:\:{p}^{\mathrm{2}} −\mathrm{2}{p}=\mathrm{0} \\ $$$$\:\:\:\:\:\:{p}−\mathrm{2}=\mathrm{0} \\ $$$$\:\:\:\:\:{p}=\mathrm{2}\:\Rightarrow{n}={p}+\mathrm{1}=\mathrm{2}+\mathrm{1}=\mathrm{3} \\ $$$$\:\:\:\:\:{m}={p}=\mathrm{2},{n}=\mathrm{3}\:\left({same}\:{result}\right) \\ $$$$\:^{\bullet} {m}={n}\:\wedge\:\left({m}+\mathrm{1}\right)\left({m}^{\mathrm{2}} −{m}+\mathrm{1}\right)={pn} \\ $$$$\:\:\:\:\left({n}+\mathrm{1}\right)\left({n}^{\mathrm{2}} −{n}+\mathrm{1}\right)={pn} \\ $$$$\:\:\:\:\:\:{n}^{\mathrm{3}} +\mathrm{1}={pn} \\ $$$$\:\:\:\:\:\:{n}^{\mathrm{2}} +\frac{\mathrm{1}}{{n}}={p} \\ $$$${Clearly}\:{p}\:{is}\:{whole}\:{number}\left({prime}\right) \\ $$$${so}\:\:{n}=\mathrm{1}\Rightarrow{m}=\mathrm{1} \\ $$$${so}\:{p}=\mathrm{2}\: \\ $$$$\left({gcd}\left(\mathrm{1}^{\mathrm{2}} −\mathrm{1}+\mathrm{1},\mathrm{1}+\mathrm{1}\right)={gcd}\left(\mathrm{1},\mathrm{2}\right)=\mathrm{1}\right) \\ $$$$\:^{\bullet} {m}={n}^{\mathrm{2}} \:\wedge\:\left({m}+\mathrm{1}\right)\left({m}^{\mathrm{2}} −{m}+\mathrm{1}\right)={p} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left({n}^{\mathrm{2}} +\mathrm{1}\right)\left({n}^{\mathrm{2}} −{n}+\mathrm{1}\right)={p} \\ $$$$\Rightarrow\:\:\:{n}^{\mathrm{2}} +\mathrm{1}=\mathrm{1}\:\wedge\:{n}^{\mathrm{2}} −{n}+\mathrm{1}={p}……\left({i}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{OR} \\ $$$$\:\:\:\:\:\:\:\:\:\:{n}^{\mathrm{2}} +\mathrm{1}={p}\:\wedge\:{n}^{\mathrm{2}} −{n}+\mathrm{1}=\mathrm{1}…..\left({ii}\right) \\ $$$$\left({i}\right)\:\:{n}=\mathrm{0}\:\wedge\:{p}=\mathrm{1}\left(\:{false}\:\because\:{p}\in\mathbb{P}\right) \\ $$$$\left({ii}\right)\:{n}^{\mathrm{2}} −{n}+\mathrm{1}=\mathrm{1}\Rightarrow{n}\left({n}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\Rightarrow{n}=\mathrm{0}\:\mid\:{n}=\mathrm{1} \\ $$$$\:\:\:\:\:{n}^{\mathrm{2}} +\mathrm{1}={p}\:\: \\ $$$$\:\:\:\:\:\:\mathrm{0}^{\mathrm{2}} +\mathrm{1}={p}\:\mid\:\mathrm{1}^{\mathrm{2}} +\mathrm{1}={p} \\ $$$$\:\:\:\:\:\:\:{p}=\mathrm{1}\:\:\:\:\:\:\:\:\:\mid\:\:{p}=\mathrm{2} \\ $$$$\:\:\:\:\:\:\left({false}\right)\:\:\:\mid\:{n}=\mathrm{1}\Rightarrow{m}={n}^{\mathrm{2}} =\mathrm{1}^{\mathrm{2}} =\mathrm{1}\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mid\:{gcd}\left(\mathrm{1}^{\mathrm{2}} −\mathrm{1}+\mathrm{1},\mathrm{1}+\mathrm{1}\right)=\mathrm{1}\: \\ $$$$……. \\ $$$$….. \\ $$$$ \\ $$$$\:\:\:\: \\ $$
Commented by mathdanisur last updated on 26/Jun/21

$${How}\:{Sir}.. \\ $$
Commented by Rasheed.Sindhi last updated on 26/Jun/21
$${On}\:{editing},\:{a}\:{great}\:{part}\:{of}\:{my}\:\:{answer}\:{has} \\ $$$${been}\:{disappeared}!!!\:{Don}'{t}\:{know} \\ $$$${why}?\:{Perhaps}\:{because}\:{my}\:{answer} \\ $$$${was}\:{too}\:{lengthy}! \\ $$
Commented by mathdanisur last updated on 26/Jun/21
$${It}'{s}\:{a}\:{pity}\:{sometimes},\:{thank}\:{you}\:{Sir} \\ $$
