Question Number 144684 by mnjuly1970 last updated on 27/Jun/21

$$ \\ $$
Answered by mindispower last updated on 27/Jun/21
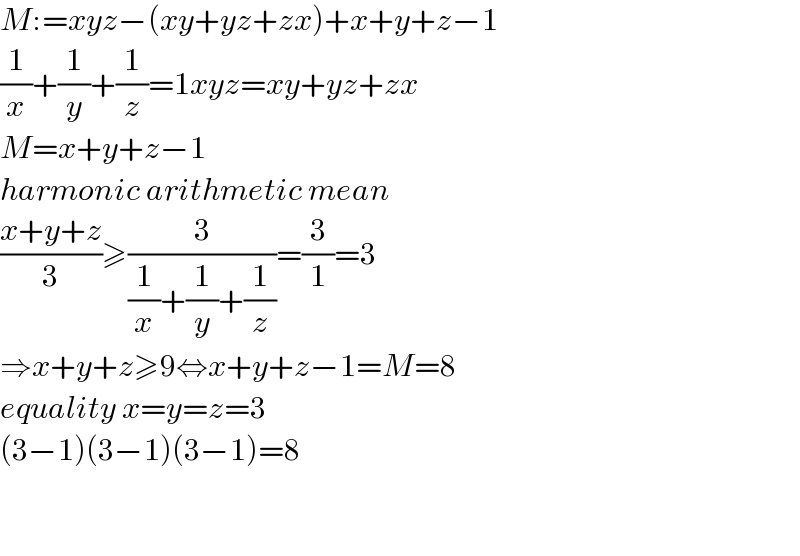
$${M}:={xyz}−\left({xy}+{yz}+{zx}\right)+{x}+{y}+{z}−\mathrm{1} \\ $$$$\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}+\frac{\mathrm{1}}{{z}}=\mathrm{1}{xyz}={xy}+{yz}+{zx} \\ $$$${M}={x}+{y}+{z}−\mathrm{1} \\ $$$${harmonic}\:{arithmetic}\:{mean} \\ $$$$\frac{{x}+{y}+{z}}{\mathrm{3}}\geqslant\frac{\mathrm{3}}{\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}+\frac{\mathrm{1}}{{z}}}=\frac{\mathrm{3}}{\mathrm{1}}=\mathrm{3} \\ $$$$\Rightarrow{x}+{y}+{z}\geqslant\mathrm{9}\Leftrightarrow{x}+{y}+{z}−\mathrm{1}={M}=\mathrm{8} \\ $$$${equality}\:{x}={y}={z}=\mathrm{3} \\ $$$$\left(\mathrm{3}−\mathrm{1}\right)\left(\mathrm{3}−\mathrm{1}\right)\left(\mathrm{3}−\mathrm{1}\right)=\mathrm{8} \\ $$$$ \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 27/Jun/21
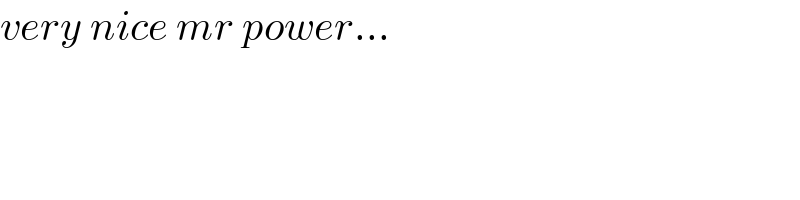
$${very}\:{nice}\:{mr}\:{power}… \\ $$
