Question Number 144753 by mondlihk last updated on 28/Jun/21

Answered by ajfour last updated on 28/Jun/21
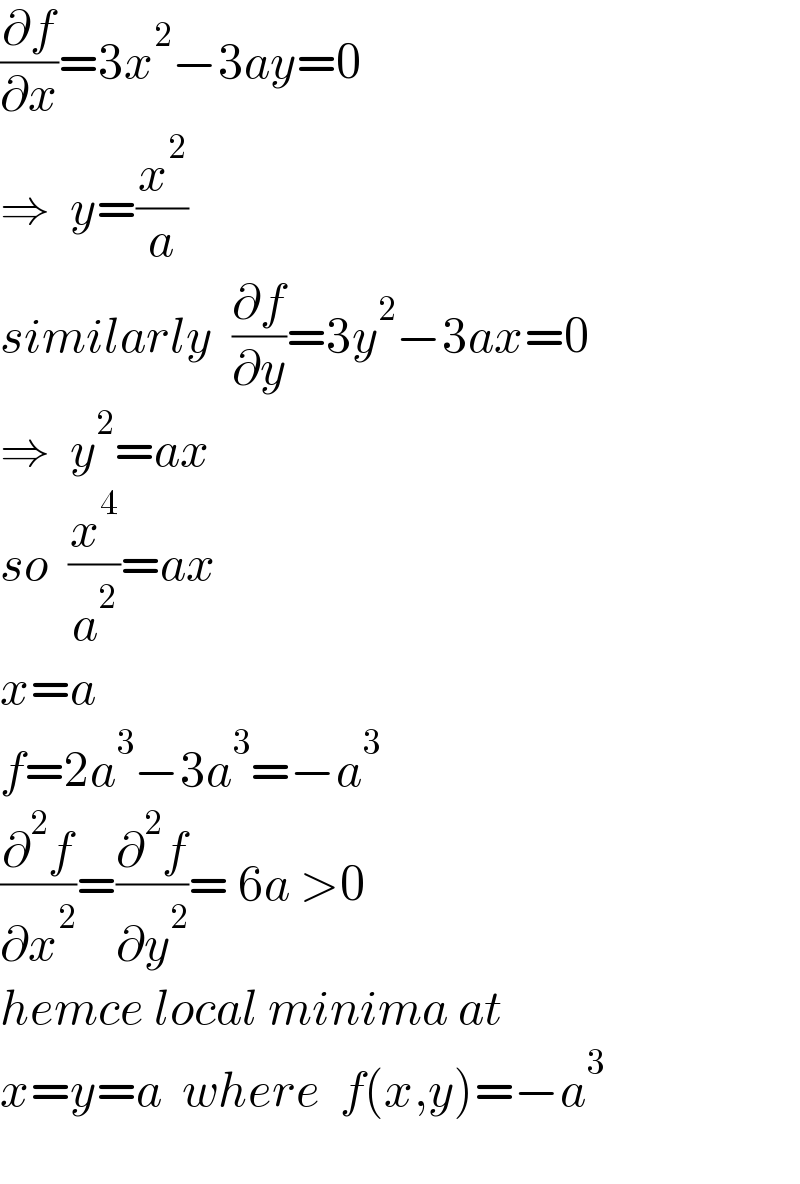
$$\frac{\partial{f}}{\partial{x}}=\mathrm{3}{x}^{\mathrm{2}} −\mathrm{3}{ay}=\mathrm{0} \\ $$$$\Rightarrow\:\:{y}=\frac{{x}^{\mathrm{2}} }{{a}} \\ $$$${similarly}\:\:\frac{\partial{f}}{\partial{y}}=\mathrm{3}{y}^{\mathrm{2}} −\mathrm{3}{ax}=\mathrm{0} \\ $$$$\Rightarrow\:\:{y}^{\mathrm{2}} ={ax}\:\: \\ $$$${so}\:\:\frac{{x}^{\mathrm{4}} }{{a}^{\mathrm{2}} }={ax} \\ $$$${x}={a} \\ $$$${f}=\mathrm{2}{a}^{\mathrm{3}} −\mathrm{3}{a}^{\mathrm{3}} =−{a}^{\mathrm{3}} \\ $$$$\frac{\partial^{\mathrm{2}} {f}}{\partial{x}^{\mathrm{2}} }=\frac{\partial^{\mathrm{2}} {f}}{\partial{y}^{\mathrm{2}} }=\:\mathrm{6}{a}\:>\mathrm{0} \\ $$$${hemce}\:{local}\:{minima}\:{at} \\ $$$${x}={y}={a}\:\:{where}\:\:{f}\left({x},{y}\right)=−{a}^{\mathrm{3}} \\ $$$$ \\ $$
