Question-144767

Question Number 144767 by mnjuly1970 last updated on 29/Jun/21

Answered by Rasheed.Sindhi last updated on 29/Jun/21

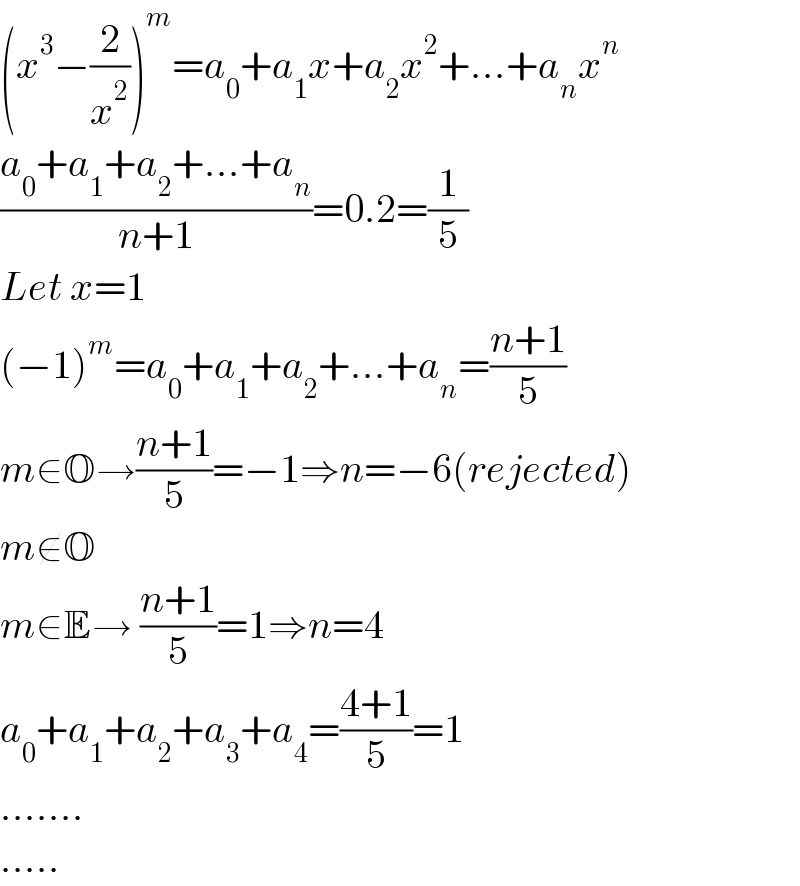
(x^3 −(2/x^2 ))^m =a_0 +a_1 x+a_2 x^2 +...+a_n x^n ((a_0 +a_1 +a_2 +...+a_n )/(n+1))=0.2=(1/5) Let x=1 (−1)^m =a_0 +a_1 +a_2 +...+a_n =((n+1)/5) m∈O→((n+1)/5)=−1⇒n=−6(rejected) m∉O m∈E→ ((n+1)/5)=1⇒n=4 a_0 +a_1 +a_2 +a_3 +a_4 =((4+1)/5)=1 ....... .....

$$\left({x}^{\mathrm{3}} −\frac{\mathrm{2}}{{x}^{\mathrm{2}} }\right)^{{m}} ={a}_{\mathrm{0}} +{a}_{\mathrm{1}} {x}+{a}_{\mathrm{2}} {x}^{\mathrm{2}} +…+{a}_{{n}} {x}^{{n}} \\ $$$$\frac{{a}_{\mathrm{0}} +{a}_{\mathrm{1}} +{a}_{\mathrm{2}} +…+{a}_{{n}} }{{n}+\mathrm{1}}=\mathrm{0}.\mathrm{2}=\frac{\mathrm{1}}{\mathrm{5}} \\ $$$${Let}\:{x}=\mathrm{1} \\ $$$$\left(−\mathrm{1}\right)^{{m}} ={a}_{\mathrm{0}} +{a}_{\mathrm{1}} +{a}_{\mathrm{2}} +…+{a}_{{n}} =\frac{{n}+\mathrm{1}}{\mathrm{5}} \\ $$$${m}\in\mathbb{O}\rightarrow\frac{{n}+\mathrm{1}}{\mathrm{5}}=−\mathrm{1}\Rightarrow{n}=−\mathrm{6}\left({rejected}\right) \\ $$$${m}\notin\mathbb{O} \\ $$$${m}\in\mathbb{E}\rightarrow\:\frac{{n}+\mathrm{1}}{\mathrm{5}}=\mathrm{1}\Rightarrow{n}=\mathrm{4} \\ $$$${a}_{\mathrm{0}} +{a}_{\mathrm{1}} +{a}_{\mathrm{2}} +{a}_{\mathrm{3}} +{a}_{\mathrm{4}} =\frac{\mathrm{4}+\mathrm{1}}{\mathrm{5}}=\mathrm{1} \\ $$$$……. \\ $$$$….. \\ $$

Answered by mr W last updated on 29/Jun/21

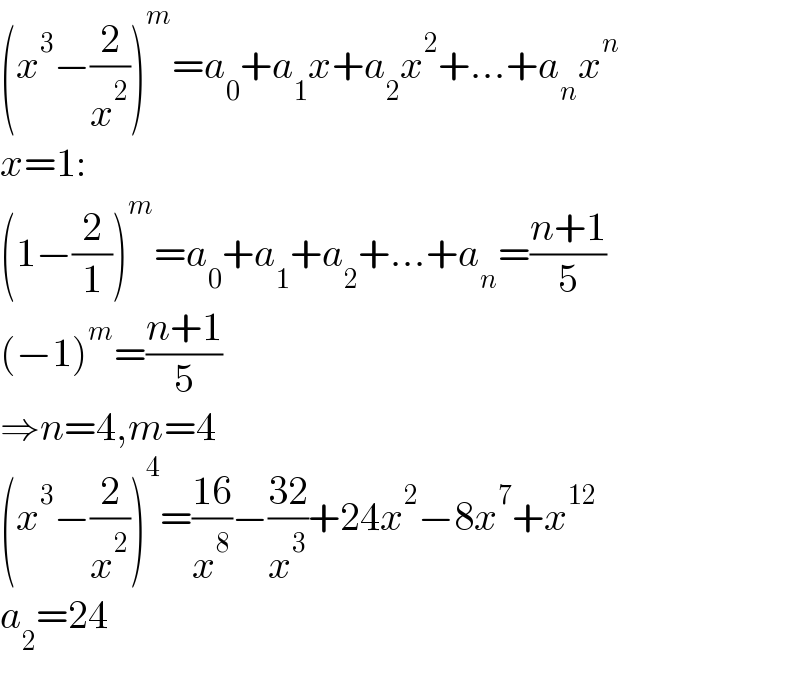
(x^3 −(2/x^2 ))^m =a_0 +a_1 x+a_2 x^2 +...+a_n x^n x=1: (1−(2/1))^m =a_0 +a_1 +a_2 +...+a_n =((n+1)/5) (−1)^m =((n+1)/5) ⇒n=4,m=4 (x^3 −(2/x^2 ))^4 =((16)/x^8 )−((32)/x^3 )+24x^2 −8x^7 +x^(12) a_2 =24

$$\left({x}^{\mathrm{3}} −\frac{\mathrm{2}}{{x}^{\mathrm{2}} }\right)^{{m}} ={a}_{\mathrm{0}} +{a}_{\mathrm{1}} {x}+{a}_{\mathrm{2}} {x}^{\mathrm{2}} +…+{a}_{{n}} {x}^{{n}} \\ $$$${x}=\mathrm{1}: \\ $$$$\left(\mathrm{1}−\frac{\mathrm{2}}{\mathrm{1}}\right)^{{m}} ={a}_{\mathrm{0}} +{a}_{\mathrm{1}} +{a}_{\mathrm{2}} +…+{a}_{{n}} =\frac{{n}+\mathrm{1}}{\mathrm{5}} \\ $$$$\left(−\mathrm{1}\right)^{{m}} =\frac{{n}+\mathrm{1}}{\mathrm{5}} \\ $$$$\Rightarrow{n}=\mathrm{4},{m}=\mathrm{4} \\ $$$$\left({x}^{\mathrm{3}} −\frac{\mathrm{2}}{{x}^{\mathrm{2}} }\right)^{\mathrm{4}} =\frac{\mathrm{16}}{{x}^{\mathrm{8}} }−\frac{\mathrm{32}}{{x}^{\mathrm{3}} }+\mathrm{24}{x}^{\mathrm{2}} −\mathrm{8}{x}^{\mathrm{7}} +{x}^{\mathrm{12}} \\ $$$${a}_{\mathrm{2}} =\mathrm{24} \\ $$

Commented by Rasheed.Sindhi last updated on 30/Jun/21

$$\mathcal{N}\:\overset{\bullet} {\shortmid}\:\subset\:\in\:\boldsymbol{\mathrm{Sir}}! \\ $$

Commented by mnjuly1970 last updated on 30/Jun/21

$$\:\:{thx}\:{mr}\:{W}… \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply