Question Number 144772 by phally last updated on 29/Jun/21

Answered by liberty last updated on 29/Jun/21
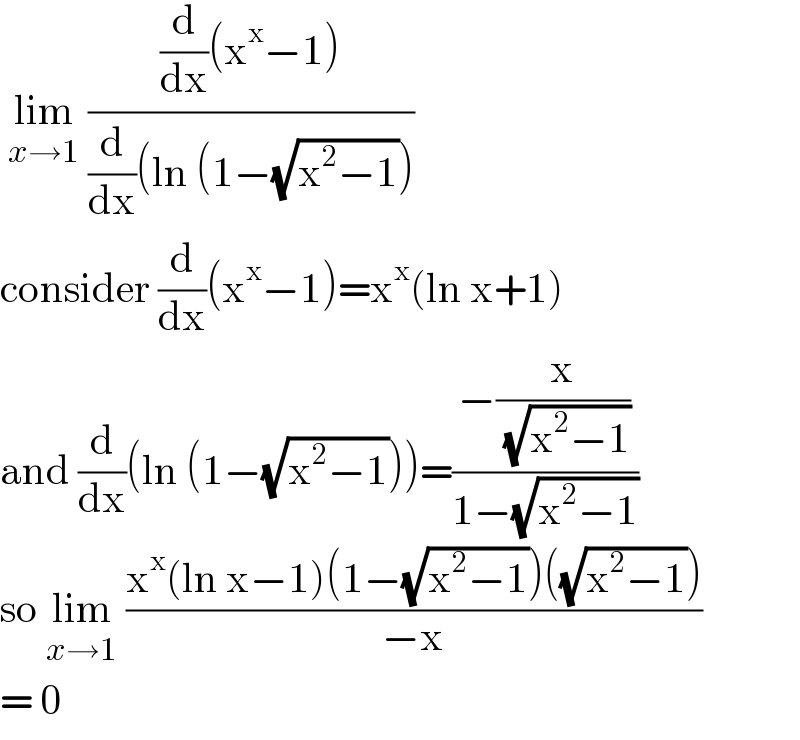
$$\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\frac{\mathrm{d}}{\mathrm{dx}}\left(\mathrm{x}^{\mathrm{x}} −\mathrm{1}\right)}{\frac{\mathrm{d}}{\mathrm{dx}}\left(\mathrm{ln}\:\left(\mathrm{1}−\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\right)\right.}\: \\ $$$$\mathrm{consider}\:\frac{\mathrm{d}}{\mathrm{dx}}\left(\mathrm{x}^{\mathrm{x}} −\mathrm{1}\right)=\mathrm{x}^{\mathrm{x}} \left(\mathrm{ln}\:\mathrm{x}+\mathrm{1}\right) \\ $$$$\mathrm{and}\:\frac{\mathrm{d}}{\mathrm{dx}}\left(\mathrm{ln}\:\left(\mathrm{1}−\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\right)\right)=\frac{−\frac{\mathrm{x}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}}}{\mathrm{1}−\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}}\: \\ $$$$\mathrm{so}\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\mathrm{x}^{\mathrm{x}} \left(\mathrm{ln}\:\mathrm{x}−\mathrm{1}\right)\left(\mathrm{1}−\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\right)\left(\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\right)}{−\mathrm{x}} \\ $$$$=\:\mathrm{0}\: \\ $$
Commented by phally last updated on 29/Jun/21

$$\:\:\:\:\mathrm{thank}\:\mathrm{brother} \\ $$
