Question Number 144777 by Nhozie last updated on 29/Jun/21

Answered by som(math1967) last updated on 29/Jun/21
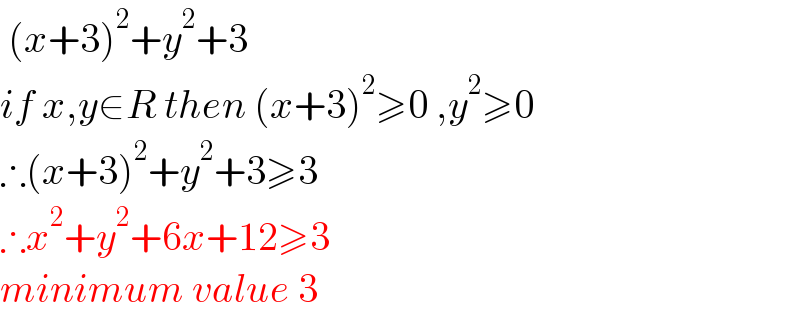
$$\:\left({x}+\mathrm{3}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{3} \\ $$$${if}\:{x},{y}\in{R}\:{then}\:\left({x}+\mathrm{3}\right)^{\mathrm{2}} \geqslant\mathrm{0}\:,{y}^{\mathrm{2}} \geqslant\mathrm{0} \\ $$$$\therefore\left({x}+\mathrm{3}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{3}\geqslant\mathrm{3} \\ $$$$\therefore{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{6}{x}+\mathrm{12}\geqslant\mathrm{3} \\ $$$${minimum}\:{value}\:\mathrm{3} \\ $$
Answered by imjagoll last updated on 29/Jun/21
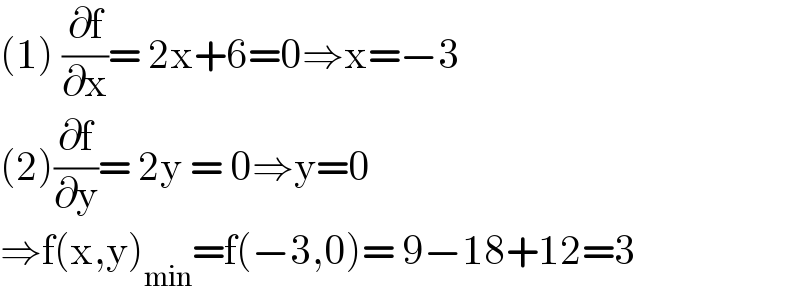
$$\left(\mathrm{1}\right)\:\frac{\partial\mathrm{f}}{\partial\mathrm{x}}=\:\mathrm{2x}+\mathrm{6}=\mathrm{0}\Rightarrow\mathrm{x}=−\mathrm{3} \\ $$$$\left(\mathrm{2}\right)\frac{\partial\mathrm{f}}{\partial\mathrm{y}}=\:\mathrm{2y}\:=\:\mathrm{0}\Rightarrow\mathrm{y}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{x},\mathrm{y}\right)_{\mathrm{min}} =\mathrm{f}\left(−\mathrm{3},\mathrm{0}\right)=\:\mathrm{9}−\mathrm{18}+\mathrm{12}=\mathrm{3} \\ $$
