Question Number 144815 by mnjuly1970 last updated on 29/Jun/21

Answered by mindispower last updated on 30/Jun/21
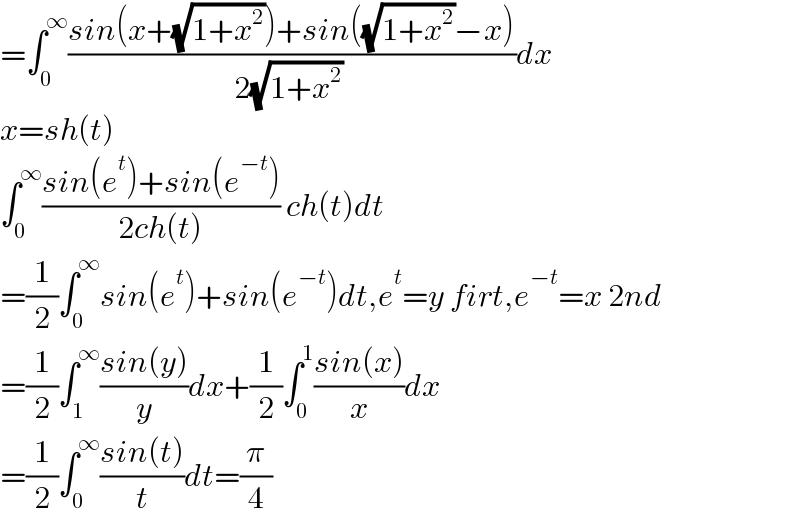
$$=\int_{\mathrm{0}} ^{\infty} \frac{{sin}\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)+{sin}\left(\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }−{x}\right)}{\mathrm{2}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:}{dx} \\ $$$${x}={sh}\left({t}\right) \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{sin}\left({e}^{{t}} \right)+{sin}\left({e}^{−{t}} \right)}{\mathrm{2}{ch}\left({t}\right)}\:{ch}\left({t}\right){dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} {sin}\left({e}^{{t}} \right)+{sin}\left({e}^{−{t}} \right){dt},{e}^{{t}} ={y}\:{firt},{e}^{−{t}} ={x}\:\mathrm{2}{nd} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{1}} ^{\infty} \frac{{sin}\left({y}\right)}{{y}}{dx}+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{sin}\left({x}\right)}{{x}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{{sin}\left({t}\right)}{{t}}{dt}=\frac{\pi}{\mathrm{4}} \\ $$
