Question Number 144875 by lapache last updated on 30/Jun/21

Answered by Dwaipayan Shikari last updated on 30/Jun/21
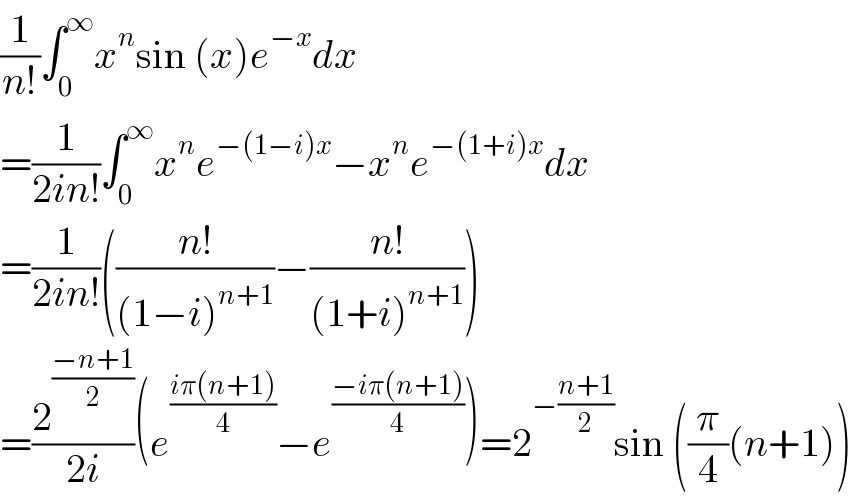
$$\frac{\mathrm{1}}{{n}!}\int_{\mathrm{0}} ^{\infty} {x}^{{n}} \mathrm{sin}\:\left({x}\right){e}^{−{x}} {dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{in}!}\int_{\mathrm{0}} ^{\infty} {x}^{{n}} {e}^{−\left(\mathrm{1}−{i}\right){x}} −{x}^{{n}} {e}^{−\left(\mathrm{1}+{i}\right){x}} {dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{in}!}\left(\frac{{n}!}{\left(\mathrm{1}−{i}\right)^{{n}+\mathrm{1}} }−\frac{{n}!}{\left(\mathrm{1}+{i}\right)^{{n}+\mathrm{1}} }\right) \\ $$$$=\frac{\mathrm{2}^{\frac{−{n}+\mathrm{1}}{\mathrm{2}}} }{\mathrm{2}{i}}\left({e}^{\frac{{i}\pi\left({n}+\mathrm{1}\right)}{\mathrm{4}}} −{e}^{\frac{−{i}\pi\left({n}+\mathrm{1}\right)}{\mathrm{4}}} \right)=\mathrm{2}^{−\frac{{n}+\mathrm{1}}{\mathrm{2}}} \mathrm{sin}\:\left(\frac{\pi}{\mathrm{4}}\left({n}+\mathrm{1}\right)\right) \\ $$
