Question Number 144936 by mathdanisur last updated on 30/Jun/21

Answered by mindispower last updated on 30/Jun/21
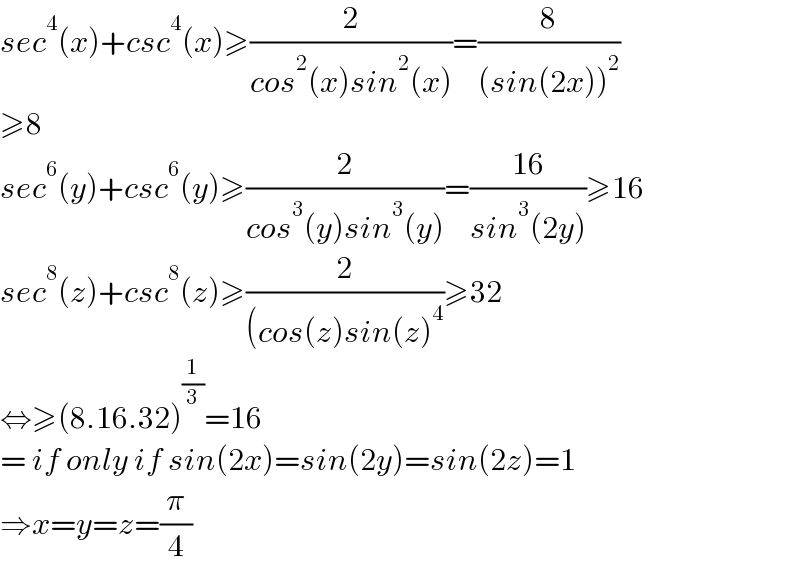
$${sec}^{\mathrm{4}} \left({x}\right)+{csc}^{\mathrm{4}} \left({x}\right)\geqslant\frac{\mathrm{2}}{{cos}^{\mathrm{2}} \left({x}\right){sin}^{\mathrm{2}} \left({x}\right)}=\frac{\mathrm{8}}{\left({sin}\left(\mathrm{2}{x}\right)\right)^{\mathrm{2}} } \\ $$$$\geqslant\mathrm{8} \\ $$$${sec}^{\mathrm{6}} \left({y}\right)+{csc}^{\mathrm{6}} \left({y}\right)\geqslant\frac{\mathrm{2}}{{cos}^{\mathrm{3}} \left({y}\right){sin}^{\mathrm{3}} \left({y}\right)}=\frac{\mathrm{16}}{{sin}^{\mathrm{3}} \left(\mathrm{2}{y}\right)}\geqslant\mathrm{16} \\ $$$${sec}^{\mathrm{8}} \left({z}\right)+{csc}^{\mathrm{8}} \left({z}\right)\geqslant\frac{\mathrm{2}}{\left({cos}\left({z}\right){sin}\left({z}\right)^{\mathrm{4}} \right.}\geqslant\mathrm{32} \\ $$$$\Leftrightarrow\geqslant\left(\mathrm{8}.\mathrm{16}.\mathrm{32}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} =\mathrm{16} \\ $$$$=\:{if}\:{only}\:{if}\:{sin}\left(\mathrm{2}{x}\right)={sin}\left(\mathrm{2}{y}\right)={sin}\left(\mathrm{2}{z}\right)=\mathrm{1} \\ $$$$\Rightarrow{x}={y}={z}=\frac{\pi}{\mathrm{4}} \\ $$
Commented by mathdanisur last updated on 30/Jun/21
$${a}\:{lot}\:{cool}\:{Ser}\:{thanks} \\ $$
