Question Number 144959 by mathdanisur last updated on 30/Jun/21

Answered by Ar Brandon last updated on 01/Jul/21
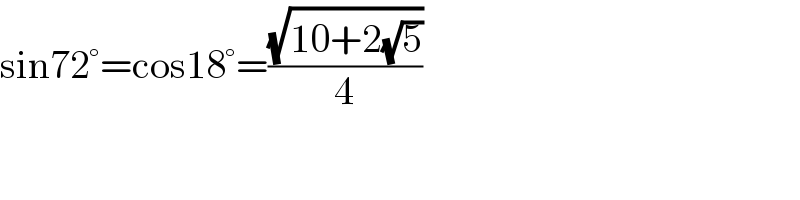
$$\mathrm{sin72}°=\mathrm{cos18}°=\frac{\sqrt{\mathrm{10}+\mathrm{2}\sqrt{\mathrm{5}}}}{\mathrm{4}} \\ $$
Commented by Ar Brandon last updated on 01/Jul/21
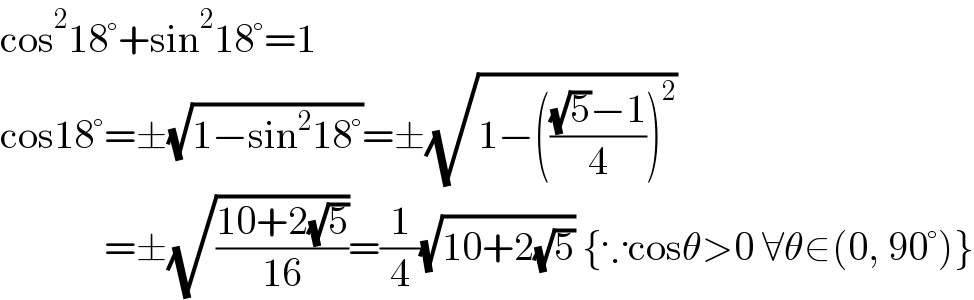
$$\mathrm{cos}^{\mathrm{2}} \mathrm{18}°+\mathrm{sin}^{\mathrm{2}} \mathrm{18}°=\mathrm{1} \\ $$$$\mathrm{cos18}°=\pm\sqrt{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \mathrm{18}°}=\pm\sqrt{\mathrm{1}−\left(\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\pm\sqrt{\frac{\mathrm{10}+\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{16}}}=\frac{\mathrm{1}}{\mathrm{4}}\sqrt{\mathrm{10}+\mathrm{2}\sqrt{\mathrm{5}}}\:\left\{\because\mathrm{cos}\theta>\mathrm{0}\:\forall\theta\in\left(\mathrm{0},\:\mathrm{90}°\right)\right\} \\ $$
Commented by mathdanisur last updated on 01/Jul/21
$${cool}\:{thankyou}\:{Sir} \\ $$
Answered by imjagoll last updated on 01/Jul/21
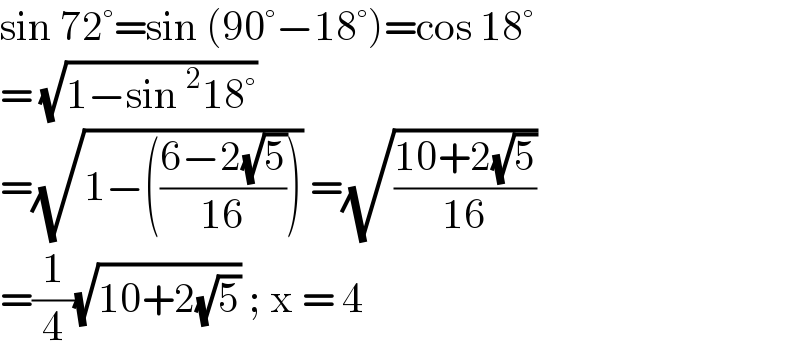
$$\mathrm{sin}\:\mathrm{72}°=\mathrm{sin}\:\left(\mathrm{90}°−\mathrm{18}°\right)=\mathrm{cos}\:\mathrm{18}° \\ $$$$=\:\sqrt{\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} \mathrm{18}°} \\ $$$$=\sqrt{\mathrm{1}−\left(\frac{\mathrm{6}−\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{16}}\right)}\:=\sqrt{\frac{\mathrm{10}+\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{16}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\sqrt{\mathrm{10}+\mathrm{2}\sqrt{\mathrm{5}}}\:;\:\mathrm{x}\:=\:\mathrm{4} \\ $$
Commented by mathdanisur last updated on 01/Jul/21

$${cool}\:{thanks}\:{Sir} \\ $$
