Question Number 144975 by mim24 last updated on 01/Jul/21
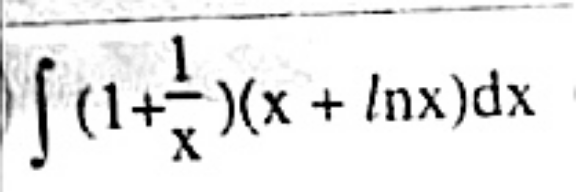
Answered by ArielVyny last updated on 01/Jul/21
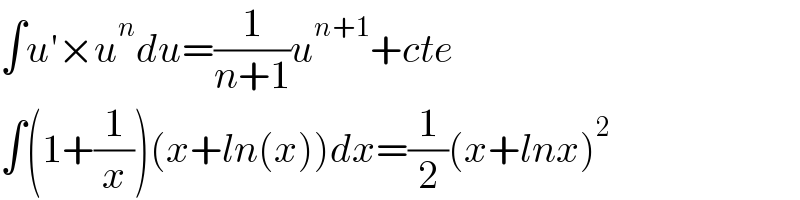
$$\int{u}'×{u}^{{n}} {du}=\frac{\mathrm{1}}{{n}+\mathrm{1}}{u}^{{n}+\mathrm{1}} +{cte} \\ $$$$\int\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)\left({x}+{ln}\left({x}\right)\right){dx}=\frac{\mathrm{1}}{\mathrm{2}}\left({x}+{lnx}\right)^{\mathrm{2}} \\ $$
Answered by som(math1967) last updated on 01/Jul/21
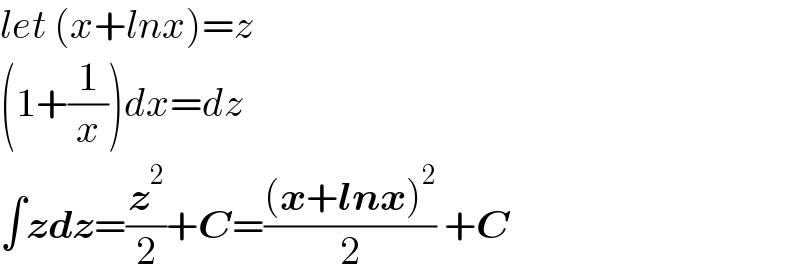
$${let}\:\left({x}+{lnx}\right)={z} \\ $$$$\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right){dx}={dz} \\ $$$$\int\boldsymbol{{zdz}}=\frac{\boldsymbol{{z}}^{\mathrm{2}} }{\mathrm{2}}+\boldsymbol{{C}}=\frac{\left(\boldsymbol{{x}}+\boldsymbol{{lnx}}\right)^{\mathrm{2}} }{\mathrm{2}}\:+\boldsymbol{{C}} \\ $$
Answered by imjagoll last updated on 01/Jul/21
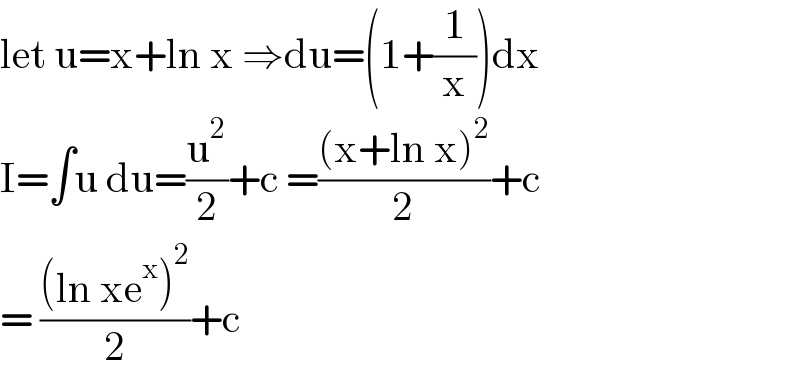
$$\mathrm{let}\:\mathrm{u}=\mathrm{x}+\mathrm{ln}\:\mathrm{x}\:\Rightarrow\mathrm{du}=\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}}\right)\mathrm{dx} \\ $$$$\mathrm{I}=\int\mathrm{u}\:\mathrm{du}=\frac{\mathrm{u}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{c}\:=\frac{\left(\mathrm{x}+\mathrm{ln}\:\mathrm{x}\right)^{\mathrm{2}} }{\mathrm{2}}+\mathrm{c} \\ $$$$=\:\frac{\left(\mathrm{ln}\:\mathrm{xe}^{\mathrm{x}} \right)^{\mathrm{2}} }{\mathrm{2}}+\mathrm{c}\: \\ $$
