Question Number 145009 by mim24 last updated on 01/Jul/21

Answered by ArielVyny last updated on 01/Jul/21
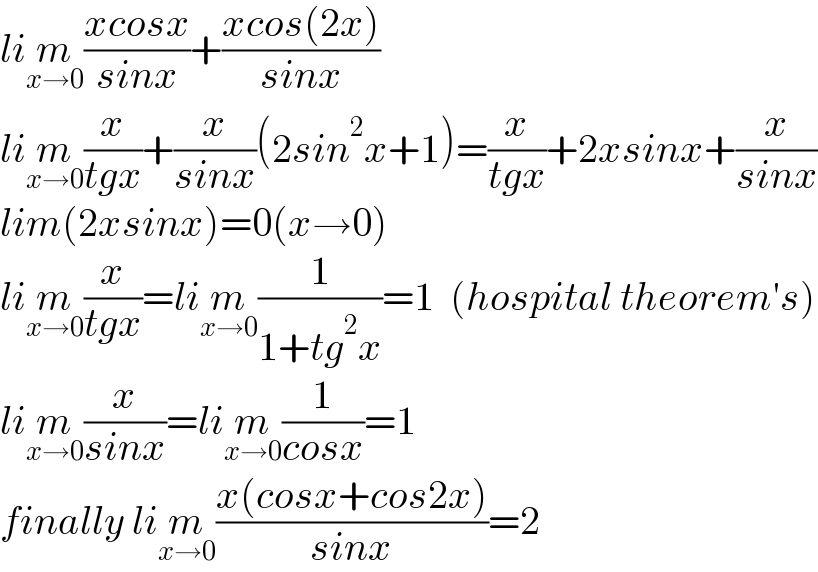
$${li}\underset{{x}\rightarrow\mathrm{0}} {{m}}\frac{{xcosx}}{{sinx}}+\frac{{xcos}\left(\mathrm{2}{x}\right)}{{sinx}} \\ $$$${li}\underset{{x}\rightarrow\mathrm{0}} {{m}}\frac{{x}}{{tgx}}+\frac{{x}}{{sinx}}\left(\mathrm{2}{sin}^{\mathrm{2}} {x}+\mathrm{1}\right)=\frac{{x}}{{tgx}}+\mathrm{2}{xsinx}+\frac{{x}}{{sinx}} \\ $$$${lim}\left(\mathrm{2}{xsinx}\right)=\mathrm{0}\left({x}\rightarrow\mathrm{0}\right) \\ $$$${li}\underset{{x}\rightarrow\mathrm{0}} {{m}}\frac{{x}}{{tgx}}={li}\underset{{x}\rightarrow\mathrm{0}} {{m}}\frac{\mathrm{1}}{\mathrm{1}+{tg}^{\mathrm{2}} {x}}=\mathrm{1}\:\:\left({hospital}\:{theorem}'{s}\right) \\ $$$${li}\underset{{x}\rightarrow\mathrm{0}} {{m}}\frac{{x}}{{sinx}}={li}\underset{{x}\rightarrow\mathrm{0}} {{m}}\frac{\mathrm{1}}{{cosx}}=\mathrm{1} \\ $$$${finally}\:{li}\underset{{x}\rightarrow\mathrm{0}} {{m}}\frac{{x}\left({cosx}+{cos}\mathrm{2}{x}\right)}{{sinx}}=\mathrm{2} \\ $$
Answered by Rasheed.Sindhi last updated on 01/Jul/21
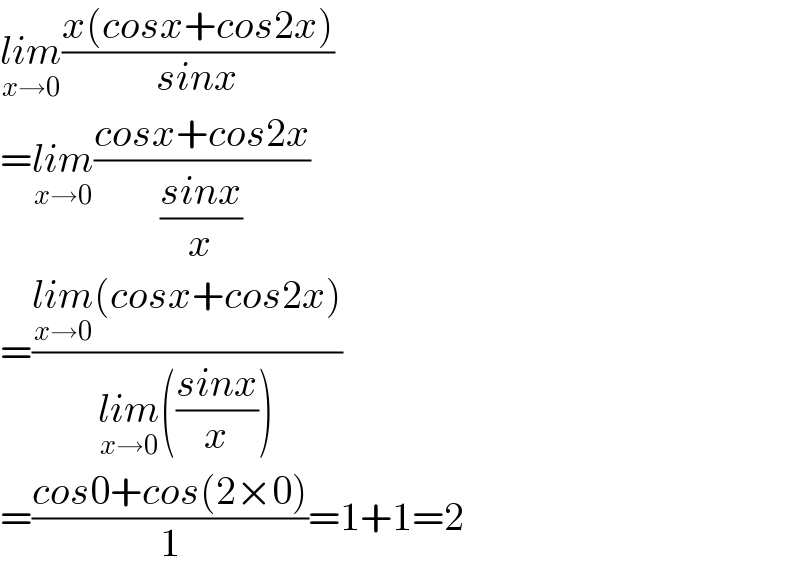
$$\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{{x}\left({cosx}+{cos}\mathrm{2}{x}\right)}{{sinx}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{{cosx}+{cos}\mathrm{2}{x}}{\frac{{sinx}}{{x}}} \\ $$$$=\frac{\underset{{x}\rightarrow\mathrm{0}} {{lim}}\left({cosx}+{cos}\mathrm{2}{x}\right)}{\underset{{x}\rightarrow\mathrm{0}} {{lim}}\left(\frac{{sinx}}{{x}}\right)} \\ $$$$=\frac{{cos}\mathrm{0}+{cos}\left(\mathrm{2}×\mathrm{0}\right)}{\mathrm{1}}=\mathrm{1}+\mathrm{1}=\mathrm{2} \\ $$
Commented by greg_ed last updated on 01/Jul/21

$$\mathrm{cool},\:\mathrm{sir}\:\mathrm{Rasheed}\:! \\ $$
Commented by Rasheed.Sindhi last updated on 01/Jul/21
$$\boldsymbol{\mathcal{T}{h}\alpha{n}\mathcal{X}}\:\:\mathrm{sir}\:\mathrm{greg\_ed}! \\ $$
Answered by mathmax by abdo last updated on 01/Jul/21

$$\mathrm{we}\:\mathrm{know}\:\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \:\frac{\mathrm{sinx}}{\mathrm{x}}=\mathrm{1}\:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \frac{\mathrm{x}}{\mathrm{sinx}}=\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{x}\smile\mathrm{0}} \frac{\mathrm{x}\left(\mathrm{cosx}\:+\mathrm{cos}\left(\mathrm{2x}\right)\right)}{\mathrm{sinx}}=\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \frac{\mathrm{x}}{\mathrm{sinx}}×\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \left(\mathrm{cosx}\:+\mathrm{cos}\left(\mathrm{2x}\right)\right) \\ $$$$=\mathrm{1}×\left(\mathrm{1}+\mathrm{1}\right)=\mathrm{2} \\ $$
