Question Number 14523 by 1kanika# last updated on 01/Jun/17

Answered by linkelly0615 last updated on 01/Jun/17
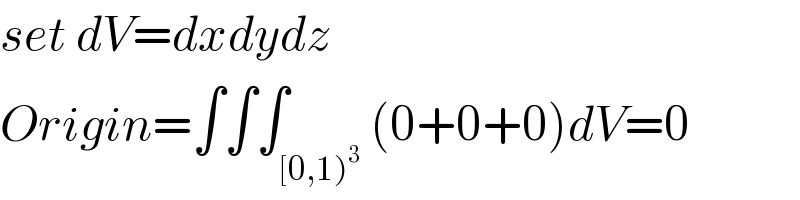
$${set}\:{dV}={dxdydz} \\ $$$${Origin}=\int\int\int_{\left[\mathrm{0},\mathrm{1}\right)^{\mathrm{3}} } \left(\mathrm{0}+\mathrm{0}+\mathrm{0}\right){dV}=\mathrm{0} \\ $$
Commented by 1kanika# last updated on 01/Jun/17

$$\mathrm{sir}\:\mathrm{the}\:\mathrm{ans}.\:\:\mathrm{is}\:\:\mathrm{3} \\ $$
Commented by linkelly0615 last updated on 02/Jun/17
![sorry....I have an overlook on the definition of [∗] . Origin=∫∫∫_((0,1]^3 ) (1+1+1)dV=3](https://www.tinkutara.com/question/Q14545.png)
$$\mathrm{sorry}….\mathrm{I}\:\mathrm{have}\:\mathrm{an}\:\mathrm{overlook} \\ $$$$\mathrm{on}\:\mathrm{the}\:\mathrm{definition}\:\mathrm{of}\:\left[\ast\right]\:. \\ $$$$ \\ $$$${Origin}=\int\int\int_{\left(\mathrm{0},\mathrm{1}\right]^{\mathrm{3}} } \left(\mathrm{1}+\mathrm{1}+\mathrm{1}\right){dV}=\mathrm{3} \\ $$
Commented by 1kanika# last updated on 02/Jun/17
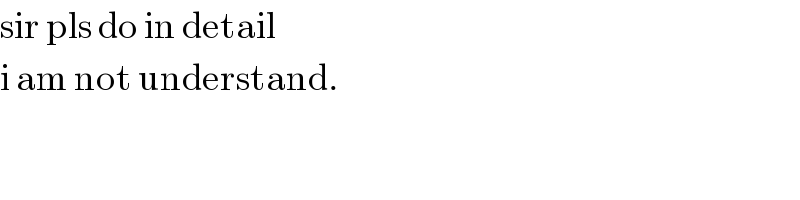
$$\mathrm{sir}\:\mathrm{pls}\:\mathrm{do}\:\mathrm{in}\:\mathrm{detail}\: \\ $$$$\mathrm{i}\:\mathrm{am}\:\mathrm{not}\:\mathrm{understand}. \\ $$
Answered by linkelly0615 last updated on 02/Jun/17
![Hint:∫_a ^a f(x)dx=0 {[x]=[y]=[z]=0, when x,y,z=0 [x]=[y]=[z]=1, when x,y,z∈(0,1]} origin= ∫_0 ^1 ∫_0 ^1 ∫_0 ^1 ([x]+[y]+[z])dxdydz {Hint:∫_0 ^1 f(x)dx=∫_0 ^a f(x)dx+∫_a ^1 f(x)dx} =lim_(h→0^+ ) {∫_0 ^h ∫_0 ^h ∫_0 ^h ([x]+[y]+[z])dxdydz+∫_h ^1 ∫_0 ^h ∫_0 ^h ([x]+[y]+[z])dxdydz +∫_0 ^h ∫_h ^1 ∫_0 ^h ([x]+[y]+[z])dxdydz+∫_0 ^h ∫_0 ^h ∫_h ^1 ([x]+[y]+[z])dxdydz +∫_h ^1 ∫_h ^1 ∫_0 ^h ([x]+[y]+[z])dxdydz+∫_0 ^h ∫_h ^1 ∫_h ^1 ([x]+[y]+[z])dxdydz +∫_h ^1 ∫_0 ^h ∫_h ^1 ([x]+[y]+[z])dxdydz+∫_h ^1 ∫_h ^1 ∫_h ^1 ([x]+[y]+[z])dxdydz } = ∫_0 ^0^+ ∫_0 ^0^+ ∫_0 ^0^+ (0+0+0)dxdydz+∫_0^+ ^1 ∫_0 ^0^+ ∫_0 ^0^+ (0+0+1)dxdydz +∫_0 ^0^+ ∫_0^+ ^1 ∫_0 ^0^+ (0+1+0)dxdydz+∫_0 ^0^+ ∫_0 ^0^+ ∫_0^+ ^1 (1+0+0)dxdydz +∫_0^+ ^1 ∫_0^+ ^1 ∫_0 ^0^+ (0+1+1)dxdydz+∫_0 ^0^+ ∫_0^+ ^1 ∫_0^+ ^1 (1+1+0)dxdydz +∫_0^+ ^1 ∫_0 ^0^+ ∫_0^+ ^1 (1+0+1)dxdydz+∫_0^+ ^1 ∫_0^+ ^1 ∫_0^+ ^1 (1+1+1)dxdydz = 0+0+0+0+0+0+0+3 =3](https://www.tinkutara.com/question/Q14549.png)
$${Hint}:\int_{{a}} ^{{a}} {f}\left({x}\right){dx}=\mathrm{0} \\ $$$$\left\{\left[{x}\right]=\left[{y}\right]=\left[{z}\right]=\mathrm{0},\:{when}\:{x},{y},{z}=\mathrm{0}\right. \\ $$$$\left.\left[{x}\right]=\left[{y}\right]=\left[{z}\right]=\mathrm{1},\:{when}\:{x},{y},{z}\in\left(\mathrm{0},\mathrm{1}\right]\right\} \\ $$$${origin}= \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{1}} \left(\left[{x}\right]+\left[{y}\right]+\left[{z}\right]\right){dxdydz} \\ $$$$\left\{{Hint}:\int_{\mathrm{0}} ^{\mathrm{1}} {f}\left({x}\right){dx}=\int_{\mathrm{0}} ^{{a}} {f}\left({x}\right){dx}+\int_{{a}} ^{\mathrm{1}} {f}\left({x}\right){dx}\right\} \\ $$$$=\underset{{h}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\left\{\int_{\mathrm{0}} ^{{h}} \int_{\mathrm{0}} ^{{h}} \int_{\mathrm{0}} ^{{h}} \left(\left[{x}\right]+\left[{y}\right]+\left[{z}\right]\right){dxdydz}+\int_{{h}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{{h}} \int_{\mathrm{0}} ^{{h}} \left(\left[{x}\right]+\left[{y}\right]+\left[{z}\right]\right){dxdydz}\right. \\ $$$$+\int_{\mathrm{0}} ^{{h}} \int_{{h}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{{h}} \left(\left[{x}\right]+\left[{y}\right]+\left[{z}\right]\right){dxdydz}+\int_{\mathrm{0}} ^{{h}} \int_{\mathrm{0}} ^{{h}} \int_{{h}} ^{\mathrm{1}} \left(\left[{x}\right]+\left[{y}\right]+\left[{z}\right]\right){dxdydz} \\ $$$$+\int_{{h}} ^{\mathrm{1}} \int_{{h}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{{h}} \left(\left[{x}\right]+\left[{y}\right]+\left[{z}\right]\right){dxdydz}+\int_{\mathrm{0}} ^{{h}} \int_{{h}} ^{\mathrm{1}} \int_{{h}} ^{\mathrm{1}} \left(\left[{x}\right]+\left[{y}\right]+\left[{z}\right]\right){dxdydz} \\ $$$$\left.+\int_{{h}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{{h}} \int_{{h}} ^{\mathrm{1}} \left(\left[{x}\right]+\left[{y}\right]+\left[{z}\right]\right){dxdydz}+\int_{{h}} ^{\mathrm{1}} \int_{{h}} ^{\mathrm{1}} \int_{{h}} ^{\mathrm{1}} \left(\left[{x}\right]+\left[{y}\right]+\left[{z}\right]\right){dxdydz}\:\right\} \\ $$$$ \\ $$$$= \\ $$$$\int_{\mathrm{0}} ^{\mathrm{0}^{+} } \int_{\mathrm{0}} ^{\mathrm{0}^{+} } \int_{\mathrm{0}} ^{\mathrm{0}^{+} } \left(\mathrm{0}+\mathrm{0}+\mathrm{0}\right){dxdydz}+\int_{\mathrm{0}^{+} } ^{\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{0}^{+} } \int_{\mathrm{0}} ^{\mathrm{0}^{+} } \left(\mathrm{0}+\mathrm{0}+\mathrm{1}\right){dxdydz} \\ $$$$+\int_{\mathrm{0}} ^{\mathrm{0}^{+} } \int_{\mathrm{0}^{+} } ^{\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{0}^{+} } \left(\mathrm{0}+\mathrm{1}+\mathrm{0}\right){dxdydz}+\int_{\mathrm{0}} ^{\mathrm{0}^{+} } \int_{\mathrm{0}} ^{\mathrm{0}^{+} } \int_{\mathrm{0}^{+} } ^{\mathrm{1}} \left(\mathrm{1}+\mathrm{0}+\mathrm{0}\right){dxdydz} \\ $$$$+\int_{\mathrm{0}^{+} } ^{\mathrm{1}} \int_{\mathrm{0}^{+} } ^{\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{0}^{+} } \left(\mathrm{0}+\mathrm{1}+\mathrm{1}\right){dxdydz}+\int_{\mathrm{0}} ^{\mathrm{0}^{+} } \int_{\mathrm{0}^{+} } ^{\mathrm{1}} \int_{\mathrm{0}^{+} } ^{\mathrm{1}} \left(\mathrm{1}+\mathrm{1}+\mathrm{0}\right){dxdydz} \\ $$$$+\int_{\mathrm{0}^{+} } ^{\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{0}^{+} } \int_{\mathrm{0}^{+} } ^{\mathrm{1}} \left(\mathrm{1}+\mathrm{0}+\mathrm{1}\right){dxdydz}+\int_{\mathrm{0}^{+} } ^{\mathrm{1}} \int_{\mathrm{0}^{+} } ^{\mathrm{1}} \int_{\mathrm{0}^{+} } ^{\mathrm{1}} \left(\mathrm{1}+\mathrm{1}+\mathrm{1}\right){dxdydz} \\ $$$$ \\ $$$$= \\ $$$$\mathrm{0}+\mathrm{0}+\mathrm{0}+\mathrm{0}+\mathrm{0}+\mathrm{0}+\mathrm{0}+\mathrm{3} \\ $$$$=\mathrm{3} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by 1kanika# last updated on 02/Jun/17

$$\mathrm{Thanks}\:\mathrm{sir} \\ $$
Commented by 1kanika# last updated on 02/Jun/17
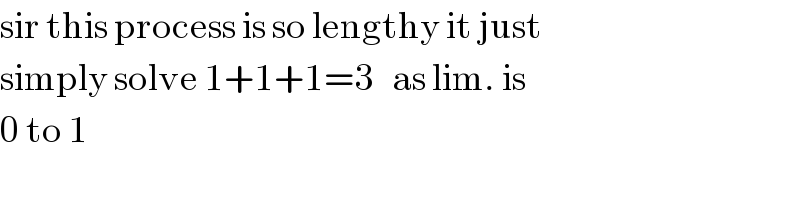
$$\mathrm{sir}\:\mathrm{this}\:\mathrm{process}\:\mathrm{is}\:\mathrm{so}\:\mathrm{lengthy}\:\mathrm{it}\:\mathrm{just}\: \\ $$$$\mathrm{simply}\:\mathrm{solve}\:\mathrm{1}+\mathrm{1}+\mathrm{1}=\mathrm{3}\:\:\:\mathrm{as}\:\mathrm{lim}.\:\mathrm{is}\: \\ $$$$\mathrm{0}\:\mathrm{to}\:\mathrm{1} \\ $$
