Question Number 145316 by imjagoll last updated on 04/Jul/21

Commented by imjagoll last updated on 04/Jul/21

$$\mathrm{interesting}\:\mathrm{problem} \\ $$$$\neq\mathrm{geometry} \\ $$
Commented by imjagoll last updated on 04/Jul/21

$$\mathrm{can}\:\mathrm{anyone}\:\mathrm{solve}\:\mathrm{this}? \\ $$
Answered by ajfour last updated on 04/Jul/21

Commented by ajfour last updated on 04/Jul/21

$${let}\:{B}\:{be}\:{the}\:{origin}\:{and}\:{x}-{axis} \\ $$$${leftwards}.\:{A}\left(\mathrm{0},{d}\right) \\ $$$${eq}.\:{of}\:{first}\:{circles} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={r}^{\mathrm{2}} \:\:\: \\ $$$$\left({x}−{d}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{1} \\ $$$${subtracting}\:{the}\:{two}\:{for}\: \\ $$$${x}\:{coordinate}\:{of}\:{point}\:{of} \\ $$$${intersection}. \\ $$$${d}\left(\mathrm{2}{p}−{d}\right)={r}^{\mathrm{2}} −\mathrm{1} \\ $$$${p}=\frac{{r}^{\mathrm{2}} +{d}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}{d}} \\ $$$${q}=\pm\sqrt{{r}^{\mathrm{2}} −{p}^{\mathrm{2}} } \\ $$$${m}=\left(\frac{{dy}}{{dx}}\right)_{{r}} =−\frac{{p}}{{q}}\: \\ $$$${s}=\left(\frac{{dy}}{{dx}}\right)_{\mathrm{2}} =\frac{{d}−{p}}{{q}} \\ $$$$\frac{{m}−{s}}{\mathrm{1}+{ms}}=\sqrt{\mathrm{3}}\:\:\:\:\:\:\left(=\mathrm{tan}\:\mathrm{60}°\right) \\ $$$${m}−{s}=\sqrt{\mathrm{3}}+\sqrt{\mathrm{3}}{ms} \\ $$$$−\frac{{p}}{{q}}−\frac{{d}−{p}}{{q}}=\sqrt{\mathrm{3}}−\sqrt{\mathrm{3}}\left(\frac{{p}}{{q}}\right)\left(\frac{{d}−{p}}{{q}}\right) \\ $$$${dq}=\sqrt{\mathrm{3}}\left({dp}−{p}^{\mathrm{2}} −{q}^{\mathrm{2}} \right) \\ $$$${d}\sqrt{{r}^{\mathrm{2}} −{p}^{\mathrm{2}} }=\sqrt{\mathrm{3}}\left({dp}−{p}^{\mathrm{2}} −{r}^{\mathrm{2}} +{p}^{\mathrm{2}} \right) \\ $$$$\Rightarrow\:{d}\sqrt{{r}^{\mathrm{2}} −{p}^{\mathrm{2}} }=\sqrt{\mathrm{3}}\left({dp}−{r}^{\mathrm{2}} \right) \\ $$$$\:\:{d}^{\mathrm{2}} \left\{{r}^{\mathrm{2}} −\left(\frac{{r}^{\mathrm{2}} +{d}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}{d}}\right)^{\mathrm{2}} \right\} \\ $$$$\:\:\:\:=\mathrm{3}\left(\frac{{r}^{\mathrm{2}} +{d}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}}−{r}^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\:{r}^{\mathrm{2}} {d}^{\mathrm{2}} −\frac{\left({r}^{\mathrm{2}} +{d}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\:\:=\frac{\mathrm{3}}{\mathrm{4}}\left({r}^{\mathrm{2}} +{d}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} +\mathrm{3}{r}^{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:−\mathrm{3}{r}^{\mathrm{2}} \left({r}^{\mathrm{2}} +{d}^{\mathrm{2}} −\mathrm{1}\right) \\ $$$$\Rightarrow \\ $$$$\left({r}^{\mathrm{2}} +{d}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} +\mathrm{3}{r}^{\mathrm{4}} \\ $$$$\:\:\:\:\:=\mathrm{3}{r}^{\mathrm{2}} \left({r}^{\mathrm{2}} +{d}^{\mathrm{2}} −\mathrm{1}\right)+{r}^{\mathrm{2}} {d}^{\mathrm{2}} \\ $$$${let}\:\:\:{d}^{\mathrm{2}} −\mathrm{1}={kr}^{\mathrm{2}} \:\:\Rightarrow \\ $$$$\left(\mathrm{1}+{k}\right)^{\mathrm{2}} +\mathrm{3}=\mathrm{3}\left(\mathrm{1}+{k}\right)+\frac{\mathrm{1}}{{r}^{\mathrm{2}} }+{k} \\ $$$$\Rightarrow\:\:{k}^{\mathrm{2}} −\mathrm{2}{k}+\mathrm{1}=\frac{\mathrm{1}}{{r}^{\mathrm{2}} }\:\:\:\:{or} \\ $$$${r}=\frac{\mathrm{1}}{{k}−\mathrm{1}} \\ $$$${d}^{\mathrm{2}} =\mathrm{1}+\left(\mathrm{1}+\frac{\mathrm{1}}{{r}}\right){r}^{\mathrm{2}} \\ $$$${d}^{\mathrm{2}} =\mathrm{1}+{r}^{\mathrm{2}} +{r} \\ $$$$\:{d}^{\mathrm{2}} =\left({r}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}} \\ $$$${d}\:{is}\:{minimum}\:{for}\:{r}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\:\:{d}_{{min}} =\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$
Answered by mr W last updated on 04/Jul/21
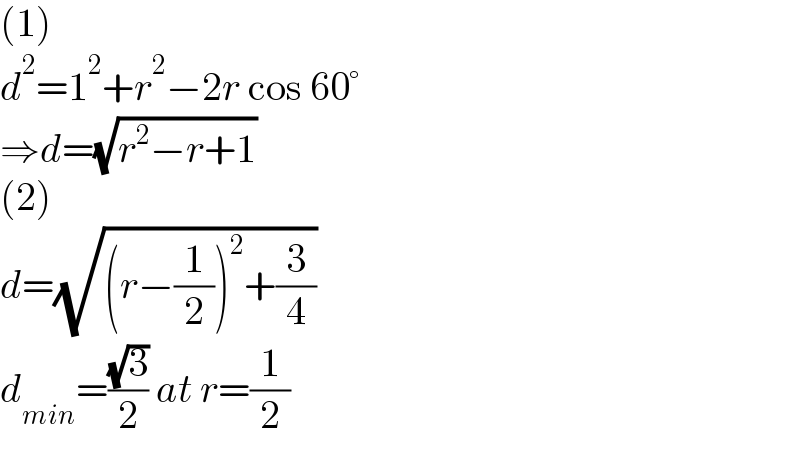
$$\left(\mathrm{1}\right) \\ $$$${d}^{\mathrm{2}} =\mathrm{1}^{\mathrm{2}} +{r}^{\mathrm{2}} −\mathrm{2}{r}\:\mathrm{cos}\:\mathrm{60}° \\ $$$$\Rightarrow{d}=\sqrt{{r}^{\mathrm{2}} −{r}+\mathrm{1}} \\ $$$$\left(\mathrm{2}\right) \\ $$$${d}=\sqrt{\left({r}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}} \\ $$$${d}_{{min}} =\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:{at}\:{r}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by mr W last updated on 04/Jul/21

Commented by mr W last updated on 04/Jul/21

$$\left(\mathrm{3}\right) \\ $$$${area}\:{of}\:{intersection}: \\ $$$$\frac{\pi}{\mathrm{2}}×\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{1}^{\mathrm{2}} }{\mathrm{2}}\left(\frac{\pi}{\mathrm{3}}−\mathrm{sin}\:\frac{\pi}{\mathrm{3}}\right) \\ $$$$=\frac{\mathrm{7}\pi}{\mathrm{24}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{4}} \\ $$
