Menu Close

Question-14535

Tinku Tara 0 Comments
Pin




Question Number 14535 by b.e.h.i.8.3.4.1.7@gmail.com last updated on 01/Jun/17
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 01/Jun/17
hello dears. this is an ancient system of equiations that have not solved by any one yet. but i think by studing several ways that used for solveing Q.14157,now we can attack this. note:it is a first time in world that quistions such that Q.14157,solved. Congraglotion to evry one in this forum! by puting: (p=x^2 ,q=y^2 ) we can write that system as below: { ((x^2 +y=a^2 )),((x+y^2 =b^2 )) :} (A) i have an idea for solving system(A). but at first i have one numeric case: { ((p+(√q)=5)),(((√p)+q=3)) :} p−4+(√q)=1⇒((√p)−2)((√p)+2)+(√q)−1=0 ((√p)−2)+((√q)−1)((√q)+1)=0⇒ ((√p)−2)=−((√q)−1)((√q)+1)⇒ −((√q)−1)((√q)+1)((√p)+2)+(√q)−1=0 ((√q)−1)(−((√q)+1)((√p)+2)+1)=0 ⇒(√q)−1=0⇒(q=1⇒p=4) but we can not use this numeric way for parameters: a^2 ,b^2 . geometric ways can useful for this. by writing system as (A),and adding equations ,we have: x^2 +x+y^2 +y=a^2 +b^2 ⇒ ⇒(x+(1/2))^2 +(y+(1/2))^2 =a^2 +b^2 +(1/2). i.e :answers of system are located on the premeter of a circle whit center point: M(((−1)/2),((−1)/2)) and radius of:R=(√(a^2 +b^2 +(1/2).)) i have a drawing in commenet below. and i want members of this forum continue my way to geting answers, or another ideas that you have. excuse me for long commenet.
$${hello}\:{dears}. \\ $$$${this}\:{is}\:{an}\:{ancient}\:{system}\:{of}\:{equiations} \\ $$$${that}\:{have}\:{not}\:{solved}\:{by}\:{any}\:{one}\:{yet}. \\ $$$${but}\:{i}\:{think}\:{by}\:{studing}\:{several}\:{ways} \\ $$$${that}\:{used}\:{for}\:{solveing}\:{Q}.\mathrm{14157},{now}\: \\ $$$${we}\:{can}\:{attack}\:{this}. \\ $$$${note}:{it}\:{is}\:{a}\:{first}\:{time}\:{in}\:{world}\:{that} \\ $$$${quistions}\:{such}\:{that}\:{Q}.\mathrm{14157},{solved}. \\ $$$${Congraglotion}\:{to}\:{evry}\:\:{one}\:{in}\:{this}\:{forum}! \\ $$$${by}\:{puting}:\:\left({p}={x}^{\mathrm{2}} ,{q}={y}^{\mathrm{2}} \right)\:{we}\:{can}\:{write} \\ $$$${that}\:{system}\:{as}\:{below}: \\ $$$$\begin{cases}{{x}^{\mathrm{2}} +{y}={a}^{\mathrm{2}} }\\{{x}+{y}^{\mathrm{2}} ={b}^{\mathrm{2}} }\end{cases}\:\:\:\:\left({A}\right) \\ $$$${i}\:{have}\:{an}\:{idea}\:{for}\:{solving}\:{system}\left({A}\right). \\ $$$${but}\:{at}\:{first}\:{i}\:{have}\:{one}\:{numeric}\:{case}: \\ $$$$\begin{cases}{{p}+\sqrt{{q}}=\mathrm{5}}\\{\sqrt{{p}}+{q}=\mathrm{3}}\end{cases} \\ $$$${p}−\mathrm{4}+\sqrt{{q}}=\mathrm{1}\Rightarrow\left(\sqrt{{p}}−\mathrm{2}\right)\left(\sqrt{{p}}+\mathrm{2}\right)+\sqrt{{q}}−\mathrm{1}=\mathrm{0} \\ $$$$\left(\sqrt{{p}}−\mathrm{2}\right)+\left(\sqrt{{q}}−\mathrm{1}\right)\left(\sqrt{{q}}+\mathrm{1}\right)=\mathrm{0}\Rightarrow \\ $$$$\left(\sqrt{{p}}−\mathrm{2}\right)=−\left(\sqrt{{q}}−\mathrm{1}\right)\left(\sqrt{{q}}+\mathrm{1}\right)\Rightarrow \\ $$$$−\left(\sqrt{{q}}−\mathrm{1}\right)\left(\sqrt{{q}}+\mathrm{1}\right)\left(\sqrt{{p}}+\mathrm{2}\right)+\sqrt{{q}}−\mathrm{1}=\mathrm{0} \\ $$$$\left(\sqrt{{q}}−\mathrm{1}\right)\left(−\left(\sqrt{{q}}+\mathrm{1}\right)\left(\sqrt{{p}}+\mathrm{2}\right)+\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow\sqrt{{q}}−\mathrm{1}=\mathrm{0}\Rightarrow\left({q}=\mathrm{1}\Rightarrow{p}=\mathrm{4}\right) \\ $$$${but}\:{we}\:{can}\:{not}\:{use}\:{this}\:{numeric}\:{way} \\ $$$${for}\:{parameters}:\:{a}^{\mathrm{2}} \:,{b}^{\mathrm{2}} . \\ $$$${geometric}\:{ways}\:{can}\:{useful}\:{for}\:{this}. \\ $$$${by}\:{writing}\:{system}\:{as}\:\left({A}\right),{and}\:{adding} \\ $$$${equations}\:,{we}\:{have}: \\ $$$${x}^{\mathrm{2}} +{x}+{y}^{\mathrm{2}} +{y}={a}^{\mathrm{2}} +{b}^{\mathrm{2}} \Rightarrow \\ $$$$\Rightarrow\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left({y}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}. \\ $$$${i}.{e}\::{answers}\:{of}\:{system}\:{are}\:{located}\:{on} \\ $$$${the}\:{premeter}\:{of}\:{a}\:{circle}\:{whit}\:{center} \\ $$$${point}:\:{M}\left(\frac{−\mathrm{1}}{\mathrm{2}},\frac{−\mathrm{1}}{\mathrm{2}}\right)\:{and}\:{radius}\:{of}:{R}=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}.} \\ $$$${i}\:{have}\:{a}\:{drawing}\:{in}\:{commenet}\:{below}. \\ $$$${and}\:{i}\:{want}\:{members}\:{of}\:{this}\:{forum} \\ $$$${continue}\:{my}\:{way}\:{to}\:{geting}\:{answers}, \\ $$$${or}\:{another}\:{ideas}\:{that}\:{you}\:{have}. \\ $$$${excuse}\:{me}\:{for}\:{long}\:{commenet}. \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 01/Jun/17
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 02/Jun/17
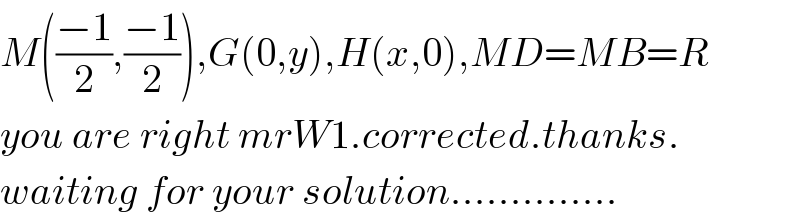
M(((−1)/2),((−1)/2)),G(0,y),H(x,0),MD=MB=R you are right mrW1.corrected.thanks. waiting for your solution..............
$${M}\left(\frac{−\mathrm{1}}{\mathrm{2}},\frac{−\mathrm{1}}{\mathrm{2}}\right),{G}\left(\mathrm{0},{y}\right),{H}\left({x},\mathrm{0}\right),{MD}={MB}={R} \\ $$$${you}\:{are}\:{right}\:{mrW}\mathrm{1}.{corrected}.{thanks}. \\ $$$${waiting}\:{for}\:{your}\:{solution}………….. \\ $$
Commented by ajfour last updated on 03/Jun/17
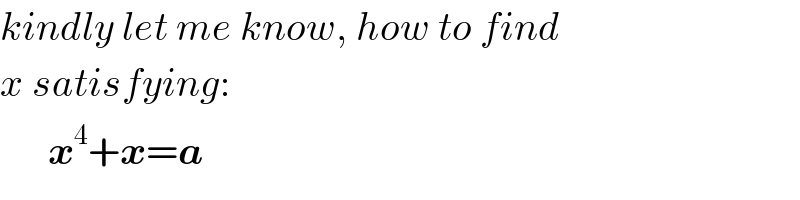
kindly let me know, how to find x satisfying: x^4 +x=a
$${kindly}\:{let}\:{me}\:{know},\:{how}\:{to}\:{find} \\ $$$${x}\:{satisfying}: \\ $$$$\:\:\:\:\:\:\boldsymbol{{x}}^{\mathrm{4}} +\boldsymbol{{x}}=\boldsymbol{{a}}\: \\ $$
Commented by mrW1 last updated on 02/Jun/17
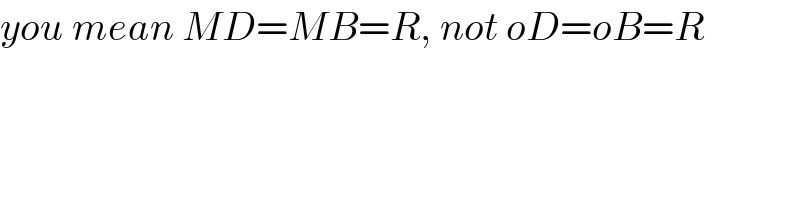
you mean MD=MB=R, not oD=oB=R
$${you}\:{mean}\:{MD}={MB}={R},\:{not}\:{oD}={oB}={R} \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 03/Jun/17
it is not easy.if a is a number,numeric methods,such that:trial and error,newton−raphson drawing a graph,my be helpful.by factrizing to: x(x+1)(x^2 −x+1)=a,and this fact that :a should dividable by x,x+1,x^2 −x+1,you can find answers. x(x+1)(x^2 −x+1)=(x^2 +x)(x^2 −x+1)= (x^2 +x)(x^2 +x−2x+1)= ⇒(x^2 +x)^2 −(2x−1)(x^2 +x)−a=0 x^2 +x=((2x−1±(√((2x−1)^2 +4a)))/2) 2x^2 +2x=2x−1±(√((2x−1)^2 +4a)) ⇒(2x^2 +1)^2 =(2x−1)^2 +(2(√a))^2 now you have a right angle triangle with sids of: 2x^2 +1,2x−1,2(√a). my be have a geometric way......
$${it}\:{is}\:{not}\:{easy}.{if}\:{a}\:{is}\:{a}\:{number},{numeric} \\ $$$${methods},{such}\:{that}:{trial}\:{and}\:{error},{newton}−{raphson} \\ $$$${drawing}\:{a}\:{graph},{my}\:{be}\:{helpful}.{by} \\ $$$${factrizing}\:{to}:\:{x}\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)={a},{and} \\ $$$${this}\:{fact}\:{that}\::{a}\:{should}\:{dividable}\:{by} \\ $$$${x},{x}+\mathrm{1},{x}^{\mathrm{2}} −{x}+\mathrm{1},{you}\:{can}\:{find}\:{answers}. \\ $$$${x}\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)=\left({x}^{\mathrm{2}} +{x}\right)\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)= \\ $$$$\left({x}^{\mathrm{2}} +{x}\right)\left({x}^{\mathrm{2}} +{x}−\mathrm{2}{x}+\mathrm{1}\right)= \\ $$$$\Rightarrow\left({x}^{\mathrm{2}} +{x}\right)^{\mathrm{2}} −\left(\mathrm{2}{x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +{x}\right)−{a}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} +{x}=\frac{\mathrm{2}{x}−\mathrm{1}\pm\sqrt{\left(\mathrm{2}{x}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{4}{a}}}{\mathrm{2}} \\ $$$$\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}{x}=\mathrm{2}{x}−\mathrm{1}\pm\sqrt{\left(\mathrm{2}{x}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{4}{a}} \\ $$$$\Rightarrow\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} =\left(\mathrm{2}{x}−\mathrm{1}\right)^{\mathrm{2}} +\left(\mathrm{2}\sqrt{{a}}\right)^{\mathrm{2}} \\ $$$${now}\:{you}\:{have}\:{a}\:{right}\:{angle}\:{triangle} \\ $$$${with}\:{sids}\:{of}:\:\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1},\mathrm{2}{x}−\mathrm{1},\mathrm{2}\sqrt{{a}}. \\ $$$${my}\:{be}\:{have}\:{a}\:{geometric}\:{way}…… \\ $$
Answered by ajfour last updated on 03/Jun/17
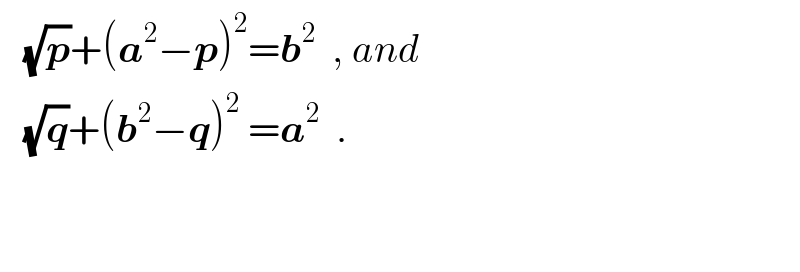
(√p)+(a^2 −p)^2 =b^2 , and (√q)+(b^2 −q)^2 =a^2 .
$$\:\:\:\sqrt{\boldsymbol{{p}}}+\left(\boldsymbol{{a}}^{\mathrm{2}} −\boldsymbol{{p}}\right)^{\mathrm{2}} =\boldsymbol{{b}}^{\mathrm{2}} \:\:,\:{and} \\ $$$$\:\:\:\sqrt{\boldsymbol{{q}}}+\left(\boldsymbol{{b}}^{\mathrm{2}} −\boldsymbol{{q}}\right)^{\mathrm{2}} \:=\boldsymbol{{a}}^{\mathrm{2}} \:\:. \\ $$$$ \\ $$$$ \\ $$
Commented by ajfour last updated on 03/Jun/17
Commented by ajfour last updated on 03/Jun/17
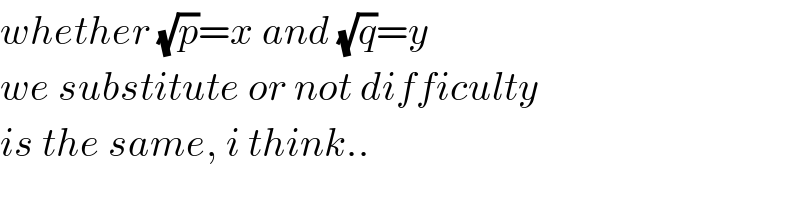
whether (√p)=x and (√q)=y we substitute or not difficulty is the same, i think..
$${whether}\:\sqrt{{p}}={x}\:{and}\:\sqrt{{q}}={y} \\ $$$${we}\:{substitute}\:{or}\:{not}\:{difficulty} \\ $$$${is}\:{the}\:{same},\:{i}\:{think}.. \\ $$
Commented by ajfour last updated on 03/Jun/17
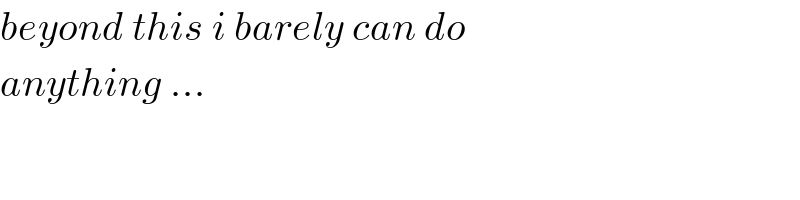
beyond this i barely can do anything ...
$${beyond}\:{this}\:{i}\:{barely}\:{can}\:{do} \\ $$$${anything}\:… \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 03/Jun/17
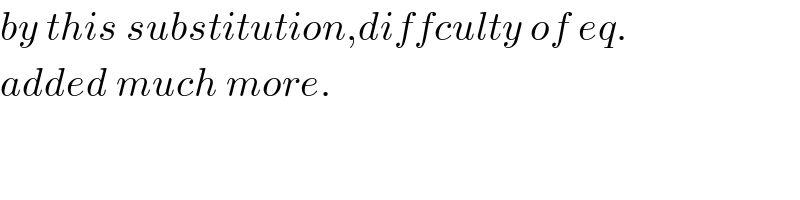
by this substitution,diffculty of eq. added much more.
$${by}\:{this}\:{substitution},{diffculty}\:{of}\:{eq}. \\ $$$${added}\:{much}\:{more}. \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 03/Jun/17
very nice pic.mrAjfour!i think there is a footage of ′golden ratio′ that can be explored.but i don′t know where and how?
$${very}\:{nice}\:{pic}.{mrAjfour}!{i}\:{think}\:{there} \\ $$$${is}\:{a}\:{footage}\:{of}\:\:'{golden}\:{ratio}'\:{that}\:{can}\:{be} \\ $$$${explored}.{but}\:{i}\:{don}'{t}\:{know}\:{where}\:{and} \\ $$$${how}? \\ $$
Commented by ajfour last updated on 03/Jun/17
thanks, can you not let me know a more definite answer to this question; what golden ratio, i have heard not.
$${thanks},\:{can}\:{you}\:{not}\:{let}\:{me}\:{know} \\ $$$${a}\:{more}\:{definite}\:\:{answer}\:{to}\:{this} \\ $$$${question};\:\:{what}\:\:{golden}\:{ratio}, \\ $$$${i}\:{have}\:{heard}\:{not}. \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 03/Jun/17
in a simple word,′golden ratio′ is the positive root of equation: ϕ(ϕ−1)=1 ϕ=((1+(√(1+4)))/2)=(((√5)+1)/2)#1.618 golden ratio is obtained when a line AB is divided by 2 part whit lengths of :a &b ,(a>b)such that ratio of greater part to whole AB is equal to ratio of smaller part to greater part.i.e:(b/(a+b))=(a/b) ⇒b^2 −ab−a^2 =0⇒b=((a+(√(5a^2 )))/2)=(((√5)+1)/2)a or: (b/a)=(((√5)+1)/2) =1.618 . golden ratio is used in very part of science and art. in architecture,design and drawing of human budy, etc..... a rectangle that have golden ratio between its sides,named as: golden rectangle.......
$${in}\:{a}\:{simple}\:{word},'{golden}\:{ratio}'\:{is}\:{the} \\ $$$${positive}\:{root}\:{of}\:{equation}:\:\:\varphi\left(\varphi−\mathrm{1}\right)=\mathrm{1} \\ $$$$\varphi=\frac{\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{4}}}{\mathrm{2}}=\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{2}}#\mathrm{1}.\mathrm{618} \\ $$$${golden}\:{ratio}\:{is}\:{obtained}\:{when}\:{a} \\ $$$${line}\:{AB}\:{is}\:{divided}\:{by}\:\mathrm{2}\:{part}\: \\ $$$${whit}\:{lengths}\:{of}\::{a}\:\&{b}\:,\left({a}>{b}\right){such}\:{that} \\ $$$${ratio}\:{of}\:{greater}\:{part}\:{to}\:{whole}\:{AB} \\ $$$${is}\:{equal}\:{to}\:{ratio}\:{of}\:{smaller}\:{part}\:{to}\: \\ $$$${greater}\:{part}.{i}.{e}:\frac{{b}}{{a}+{b}}=\frac{{a}}{{b}} \\ $$$$\Rightarrow{b}^{\mathrm{2}} −{ab}−{a}^{\mathrm{2}} =\mathrm{0}\Rightarrow{b}=\frac{{a}+\sqrt{\mathrm{5}{a}^{\mathrm{2}} }}{\mathrm{2}}=\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{2}}{a} \\ $$$${or}:\:\:\frac{{b}}{{a}}=\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{2}}\:\:=\mathrm{1}.\mathrm{618}\:. \\ $$$${golden}\:{ratio}\:{is}\:{used}\:\:{in} \\ $$$${very}\:{part}\:{of}\:{science}\:{and}\:{art}.\: \\ $$$${in}\:{architecture},{design}\:{and}\:{drawing} \\ $$$${of}\:{human}\:{budy},\:{etc}….. \\ $$$${a}\:{rectangle}\:{that}\:{have}\:{golden}\:{ratio}\: \\ $$$${between}\:{its}\:{sides},{named}\:{as}: \\ $$$${golden}\:{rectangle}……. \\ $$
Answered by mr W last updated on 05/Aug/19
let x=(√p), y=(√q) let u=a^2 , v=b^2 x^2 +y=u x+y^2 =v x+(u−x^2 )^2 =v ⇒x^4 −2ux^2 +x+u^2 −v=0 trying to use method from ajfour sir: a=−2u b=1 c=u^2 −v ⇒x^2 −px+(1/2)(−2u+p^2 +(1/p))=0 ⇒x=(1/2)(p±(√(4u−p^2 −(2/p)))) where p^2 =P with P^3 −4uP^2 +4vP−1=0 let P=Q+((4u)/3) Q^3 +3(((4u)/3))Q^2 +3(((4u)/3))^2 Q+(((4u)/3))^3 −4u[Q^2 +2(((4u)/3))Q+(((4u)/3))^2 ]+4v(Q+((4u)/3))−1=0 Q^3 +4(v−((4u^2 )/3))Q+((16uv)/3)−1=0 Δ=[(4/3)(v−((4u^2 )/3))]^3 +[(1/2)(((16uv)/3)−1)]^2 Δ=((64)/(729))(3v−4u^2 )^3 +(1/(36))(16uv−3)^2 >0, say Q=(((√Δ)−(1/6)(16uv−3)))^(1/3) −(((√Δ)+(1/6)(16uv−3)))^(1/3) P=p^2 =((4u)/3)+(((√Δ)−(1/6)(16uv−3)))^(1/3) −(((√Δ)+(1/6)(16uv−3)))^(1/3) ⇒p=±(√(((4u)/3)+(((√Δ)−(1/6)(16uv−3)))^(1/3) −(((√Δ)+(1/6)(16uv−3)))^(1/3) )) ⇒x=(1/2){±(√(((4u)/3)+(((√Δ)−(1/6)(16uv−3)))^(1/3) −(((√Δ)+(1/6)(16uv−3)))^(1/3) ))±(√(((8u)/3)−(((√Δ)−(1/6)(16uv−3)))^(1/3) +(((√Δ)+(1/6)(16uv−3)))^(1/3) ∓(2/( (√(((4u)/3)+(((√Δ)−(1/6)(16uv−3)))^(1/3) −(((√Δ)+(1/6)(16uv−3)))^(1/3) ))))))} ⇒p=(1/4){±(√(((4a^2 )/3)+(((√Δ)−(1/6)(16a^2 b^2 −3)))^(1/3) −(((√Δ)+(1/6)(16a^2 b^2 −3)))^(1/3) ))±(√(((8a^2 )/3)−(((√Δ)−(1/6)(16a^2 b^2 −3)))^(1/3) +(((√Δ)+(1/6)(16a^2 b^2 −3)))^(1/3) ∓(2/( (√(((4a^2 )/3)+(((√Δ)−(1/6)(16a^2 b^2 −3)))^(1/3) −(((√Δ)+(1/6)(16a^2 b^2 −3)))^(1/3) ))))))}^2 with Δ=((64)/(729))(3b^2 −4a^4 )^3 +(1/(36))(16a^2 b^2 −3)^2
$${let}\:{x}=\sqrt{{p}},\:{y}=\sqrt{{q}} \\ $$$${let}\:{u}={a}^{\mathrm{2}} ,\:{v}={b}^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} +{y}={u} \\ $$$${x}+{y}^{\mathrm{2}} ={v} \\ $$$${x}+\left({u}−{x}^{\mathrm{2}} \right)^{\mathrm{2}} ={v} \\ $$$$\Rightarrow{x}^{\mathrm{4}} −\mathrm{2}{ux}^{\mathrm{2}} +{x}+{u}^{\mathrm{2}} −{v}=\mathrm{0} \\ $$$${trying}\:{to}\:{use}\:{method}\:{from}\:{ajfour}\:{sir}: \\ $$$${a}=−\mathrm{2}{u} \\ $$$${b}=\mathrm{1} \\ $$$${c}={u}^{\mathrm{2}} −{v} \\ $$$$\Rightarrow{x}^{\mathrm{2}} −{px}+\frac{\mathrm{1}}{\mathrm{2}}\left(−\mathrm{2}{u}+{p}^{\mathrm{2}} +\frac{\mathrm{1}}{{p}}\right)=\mathrm{0} \\ $$$$\Rightarrow{x}=\frac{\mathrm{1}}{\mathrm{2}}\left({p}\pm\sqrt{\mathrm{4}{u}−{p}^{\mathrm{2}} −\frac{\mathrm{2}}{{p}}}\right) \\ $$$${where}\:{p}^{\mathrm{2}} ={P}\:{with} \\ $$$${P}^{\mathrm{3}} −\mathrm{4}{uP}^{\mathrm{2}} +\mathrm{4}{vP}−\mathrm{1}=\mathrm{0} \\ $$$${let}\:{P}={Q}+\frac{\mathrm{4}{u}}{\mathrm{3}} \\ $$$${Q}^{\mathrm{3}} +\mathrm{3}\left(\frac{\mathrm{4}{u}}{\mathrm{3}}\right){Q}^{\mathrm{2}} +\mathrm{3}\left(\frac{\mathrm{4}{u}}{\mathrm{3}}\right)^{\mathrm{2}} {Q}+\left(\frac{\mathrm{4}{u}}{\mathrm{3}}\right)^{\mathrm{3}} −\mathrm{4}{u}\left[{Q}^{\mathrm{2}} +\mathrm{2}\left(\frac{\mathrm{4}{u}}{\mathrm{3}}\right){Q}+\left(\frac{\mathrm{4}{u}}{\mathrm{3}}\right)^{\mathrm{2}} \right]+\mathrm{4}{v}\left({Q}+\frac{\mathrm{4}{u}}{\mathrm{3}}\right)−\mathrm{1}=\mathrm{0} \\ $$$${Q}^{\mathrm{3}} +\mathrm{4}\left({v}−\frac{\mathrm{4}{u}^{\mathrm{2}} }{\mathrm{3}}\right){Q}+\frac{\mathrm{16}{uv}}{\mathrm{3}}−\mathrm{1}=\mathrm{0} \\ $$$$\Delta=\left[\frac{\mathrm{4}}{\mathrm{3}}\left({v}−\frac{\mathrm{4}{u}^{\mathrm{2}} }{\mathrm{3}}\right)\right]^{\mathrm{3}} +\left[\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{16}{uv}}{\mathrm{3}}−\mathrm{1}\right)\right]^{\mathrm{2}} \\ $$$$\Delta=\frac{\mathrm{64}}{\mathrm{729}}\left(\mathrm{3}{v}−\mathrm{4}{u}^{\mathrm{2}} \right)^{\mathrm{3}} +\frac{\mathrm{1}}{\mathrm{36}}\left(\mathrm{16}{uv}−\mathrm{3}\right)^{\mathrm{2}} >\mathrm{0},\:{say} \\ $$$${Q}=\sqrt[{\mathrm{3}}]{\sqrt{\Delta}−\frac{\mathrm{1}}{\mathrm{6}}\left(\mathrm{16}{uv}−\mathrm{3}\right)}−\sqrt[{\mathrm{3}}]{\sqrt{\Delta}+\frac{\mathrm{1}}{\mathrm{6}}\left(\mathrm{16}{uv}−\mathrm{3}\right)} \\ $$$${P}={p}^{\mathrm{2}} =\frac{\mathrm{4}{u}}{\mathrm{3}}+\sqrt[{\mathrm{3}}]{\sqrt{\Delta}−\frac{\mathrm{1}}{\mathrm{6}}\left(\mathrm{16}{uv}−\mathrm{3}\right)}−\sqrt[{\mathrm{3}}]{\sqrt{\Delta}+\frac{\mathrm{1}}{\mathrm{6}}\left(\mathrm{16}{uv}−\mathrm{3}\right)} \\ $$$$\Rightarrow{p}=\pm\sqrt{\frac{\mathrm{4}{u}}{\mathrm{3}}+\sqrt[{\mathrm{3}}]{\sqrt{\Delta}−\frac{\mathrm{1}}{\mathrm{6}}\left(\mathrm{16}{uv}−\mathrm{3}\right)}−\sqrt[{\mathrm{3}}]{\sqrt{\Delta}+\frac{\mathrm{1}}{\mathrm{6}}\left(\mathrm{16}{uv}−\mathrm{3}\right)}} \\ $$$$\Rightarrow{x}=\frac{\mathrm{1}}{\mathrm{2}}\left\{\pm\sqrt{\frac{\mathrm{4}{u}}{\mathrm{3}}+\sqrt[{\mathrm{3}}]{\sqrt{\Delta}−\frac{\mathrm{1}}{\mathrm{6}}\left(\mathrm{16}{uv}−\mathrm{3}\right)}−\sqrt[{\mathrm{3}}]{\sqrt{\Delta}+\frac{\mathrm{1}}{\mathrm{6}}\left(\mathrm{16}{uv}−\mathrm{3}\right)}}\pm\sqrt{\frac{\mathrm{8}{u}}{\mathrm{3}}−\sqrt[{\mathrm{3}}]{\sqrt{\Delta}−\frac{\mathrm{1}}{\mathrm{6}}\left(\mathrm{16}{uv}−\mathrm{3}\right)}+\sqrt[{\mathrm{3}}]{\sqrt{\Delta}+\frac{\mathrm{1}}{\mathrm{6}}\left(\mathrm{16}{uv}−\mathrm{3}\right)}\mp\frac{\mathrm{2}}{\:\sqrt{\frac{\mathrm{4}{u}}{\mathrm{3}}+\sqrt[{\mathrm{3}}]{\sqrt{\Delta}−\frac{\mathrm{1}}{\mathrm{6}}\left(\mathrm{16}{uv}−\mathrm{3}\right)}−\sqrt[{\mathrm{3}}]{\sqrt{\Delta}+\frac{\mathrm{1}}{\mathrm{6}}\left(\mathrm{16}{uv}−\mathrm{3}\right)}}}}\right\} \\ $$$$\Rightarrow{p}=\frac{\mathrm{1}}{\mathrm{4}}\left\{\pm\sqrt{\frac{\mathrm{4}{a}^{\mathrm{2}} }{\mathrm{3}}+\sqrt[{\mathrm{3}}]{\sqrt{\Delta}−\frac{\mathrm{1}}{\mathrm{6}}\left(\mathrm{16}{a}^{\mathrm{2}} {b}^{\mathrm{2}} −\mathrm{3}\right)}−\sqrt[{\mathrm{3}}]{\sqrt{\Delta}+\frac{\mathrm{1}}{\mathrm{6}}\left(\mathrm{16}{a}^{\mathrm{2}} {b}^{\mathrm{2}} −\mathrm{3}\right)}}\pm\sqrt{\frac{\mathrm{8}{a}^{\mathrm{2}} }{\mathrm{3}}−\sqrt[{\mathrm{3}}]{\sqrt{\Delta}−\frac{\mathrm{1}}{\mathrm{6}}\left(\mathrm{16}{a}^{\mathrm{2}} {b}^{\mathrm{2}} −\mathrm{3}\right)}+\sqrt[{\mathrm{3}}]{\sqrt{\Delta}+\frac{\mathrm{1}}{\mathrm{6}}\left(\mathrm{16}{a}^{\mathrm{2}} {b}^{\mathrm{2}} −\mathrm{3}\right)}\mp\frac{\mathrm{2}}{\:\sqrt{\frac{\mathrm{4}{a}^{\mathrm{2}} }{\mathrm{3}}+\sqrt[{\mathrm{3}}]{\sqrt{\Delta}−\frac{\mathrm{1}}{\mathrm{6}}\left(\mathrm{16}{a}^{\mathrm{2}} {b}^{\mathrm{2}} −\mathrm{3}\right)}−\sqrt[{\mathrm{3}}]{\sqrt{\Delta}+\frac{\mathrm{1}}{\mathrm{6}}\left(\mathrm{16}{a}^{\mathrm{2}} {b}^{\mathrm{2}} −\mathrm{3}\right)}}}}\right\}^{\mathrm{2}} \\ $$$${with}\:\Delta=\frac{\mathrm{64}}{\mathrm{729}}\left(\mathrm{3}{b}^{\mathrm{2}} −\mathrm{4}{a}^{\mathrm{4}} \right)^{\mathrm{3}} +\frac{\mathrm{1}}{\mathrm{36}}\left(\mathrm{16}{a}^{\mathrm{2}} {b}^{\mathrm{2}} −\mathrm{3}\right)^{\mathrm{2}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *