Question Number 145423 by olalekan2 last updated on 04/Jul/21

Answered by Olaf_Thorendsen last updated on 04/Jul/21
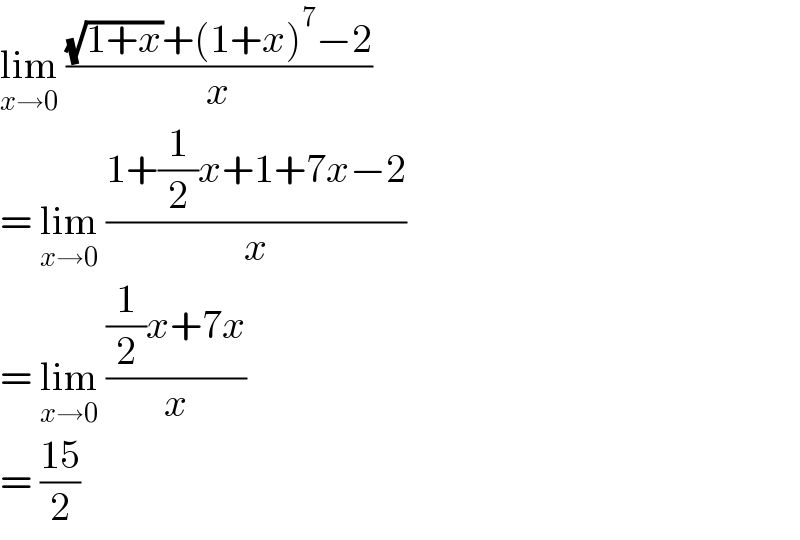
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{1}+{x}}+\left(\mathrm{1}+{x}\right)^{\mathrm{7}} −\mathrm{2}}{{x}} \\ $$$$=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}{x}+\mathrm{1}+\mathrm{7}{x}−\mathrm{2}}{{x}} \\ $$$$=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{\mathrm{1}}{\mathrm{2}}{x}+\mathrm{7}{x}}{{x}} \\ $$$$=\:\frac{\mathrm{15}}{\mathrm{2}} \\ $$
Answered by puissant last updated on 04/Jul/21
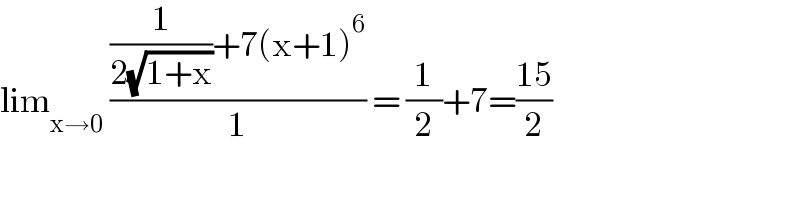
$$\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \:\frac{\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{1}+\mathrm{x}}}+\mathrm{7}\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{6}} }{\mathrm{1}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{7}=\frac{\mathrm{15}}{\mathrm{2}} \\ $$
