Question-145588

Question Number 145588 by naka3546 last updated on 06/Jul/21

Answered by chengulapetrom last updated on 06/Jul/21

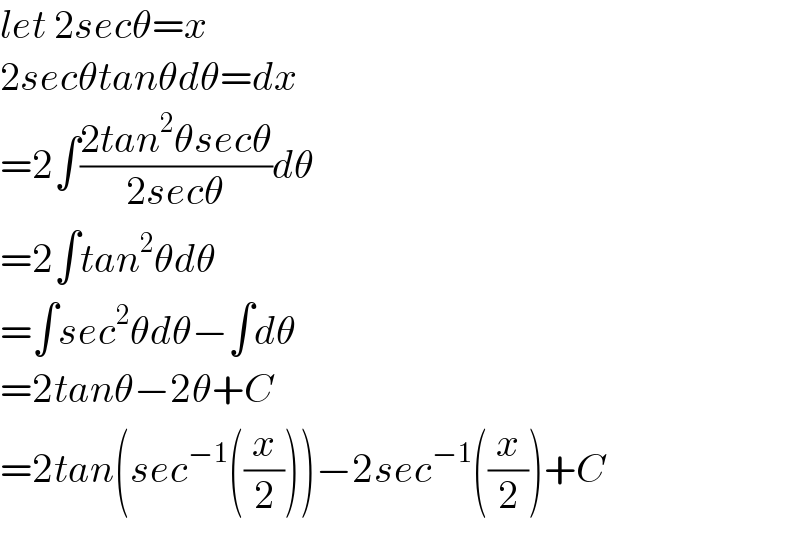
let 2secθ=x 2secθtanθdθ=dx =2∫((2tan^2 θsecθ)/(2secθ))dθ =2∫tan^2 θdθ =∫sec^2 θdθ−∫dθ =2tanθ−2θ+C =2tan(sec^(−1) ((x/2)))−2sec^(−1) ((x/2))+C

$${let}\:\mathrm{2}{sec}\theta={x} \\ $$$$\mathrm{2}{sec}\theta{tan}\theta{d}\theta={dx} \\ $$$$=\mathrm{2}\int\frac{\mathrm{2}{tan}^{\mathrm{2}} \theta{sec}\theta}{\mathrm{2}{sec}\theta}{d}\theta \\ $$$$=\mathrm{2}\int{tan}^{\mathrm{2}} \theta{d}\theta \\ $$$$=\int{sec}^{\mathrm{2}} \theta{d}\theta−\int{d}\theta \\ $$$$=\mathrm{2}{tan}\theta−\mathrm{2}\theta+{C} \\ $$$$=\mathrm{2}{tan}\left({sec}^{−\mathrm{1}} \left(\frac{{x}}{\mathrm{2}}\right)\right)−\mathrm{2}{sec}^{−\mathrm{1}} \left(\frac{{x}}{\mathrm{2}}\right)+{C} \\ $$

Answered by qaz last updated on 06/Jul/21

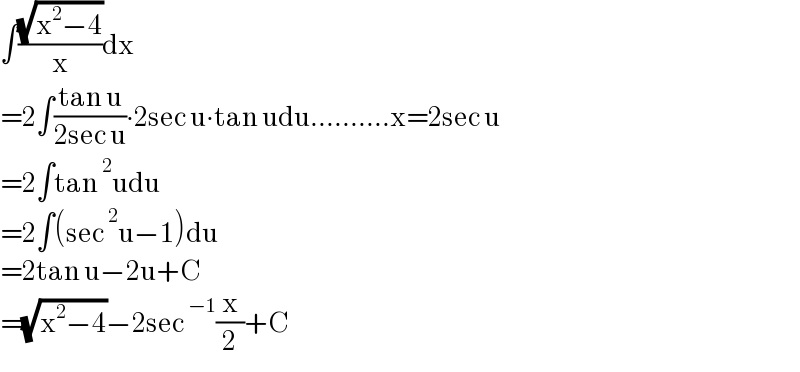
∫((√(x^2 −4))/x)dx =2∫((tan u)/(2sec u))∙2sec u∙tan udu..........x=2sec u =2∫tan^2 udu =2∫(sec^2 u−1)du =2tan u−2u+C =(√(x^2 −4))−2sec^(−1) (x/2)+C

$$\int\frac{\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{4}}}{\mathrm{x}}\mathrm{dx} \\ $$$$=\mathrm{2}\int\frac{\mathrm{tan}\:\mathrm{u}}{\mathrm{2sec}\:\mathrm{u}}\centerdot\mathrm{2sec}\:\mathrm{u}\centerdot\mathrm{tan}\:\mathrm{udu}……….\mathrm{x}=\mathrm{2sec}\:\mathrm{u} \\ $$$$=\mathrm{2}\int\mathrm{tan}\:^{\mathrm{2}} \mathrm{udu} \\ $$$$=\mathrm{2}\int\left(\mathrm{sec}\:^{\mathrm{2}} \mathrm{u}−\mathrm{1}\right)\mathrm{du} \\ $$$$=\mathrm{2tan}\:\mathrm{u}−\mathrm{2u}+\mathrm{C} \\ $$$$=\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{4}}−\mathrm{2sec}\:^{−\mathrm{1}} \frac{\mathrm{x}}{\mathrm{2}}+\mathrm{C} \\ $$

Answered by puissant last updated on 06/Jul/21

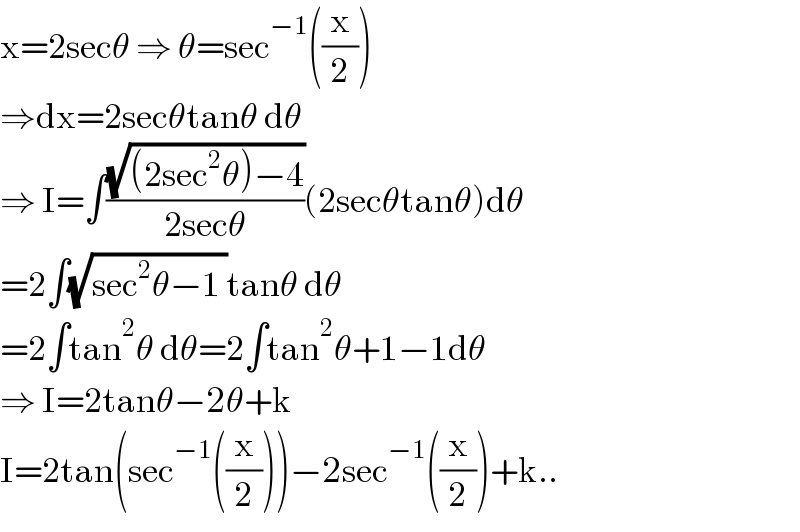
x=2secθ ⇒ θ=sec^(−1) ((x/2)) ⇒dx=2secθtanθ dθ ⇒ I=∫((√((2sec^2 θ)−4))/(2secθ))(2secθtanθ)dθ =2∫(√(sec^2 θ−1 ))tanθ dθ =2∫tan^2 θ dθ=2∫tan^2 θ+1−1dθ ⇒ I=2tanθ−2θ+k I=2tan(sec^(−1) ((x/2)))−2sec^(−1) ((x/2))+k..

$$\mathrm{x}=\mathrm{2sec}\theta\:\Rightarrow\:\theta=\mathrm{sec}^{−\mathrm{1}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right) \\ $$$$\Rightarrow\mathrm{dx}=\mathrm{2sec}\theta\mathrm{tan}\theta\:\mathrm{d}\theta \\ $$$$\Rightarrow\:\mathrm{I}=\int\frac{\sqrt{\left(\mathrm{2sec}^{\mathrm{2}} \theta\right)−\mathrm{4}}}{\mathrm{2sec}\theta}\left(\mathrm{2sec}\theta\mathrm{tan}\theta\right)\mathrm{d}\theta \\ $$$$=\mathrm{2}\int\sqrt{\mathrm{sec}^{\mathrm{2}} \theta−\mathrm{1}\:}\mathrm{tan}\theta\:\mathrm{d}\theta \\ $$$$=\mathrm{2}\int\mathrm{tan}^{\mathrm{2}} \theta\:\mathrm{d}\theta=\mathrm{2}\int\mathrm{tan}^{\mathrm{2}} \theta+\mathrm{1}−\mathrm{1d}\theta \\ $$$$\Rightarrow\:\mathrm{I}=\mathrm{2tan}\theta−\mathrm{2}\theta+\mathrm{k} \\ $$$$\mathrm{I}=\mathrm{2tan}\left(\mathrm{sec}^{−\mathrm{1}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right)\right)−\mathrm{2sec}^{−\mathrm{1}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right)+\mathrm{k}.. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply