Question Number 145660 by imjagoll last updated on 07/Jul/21

Answered by Olaf_Thorendsen last updated on 08/Jul/21
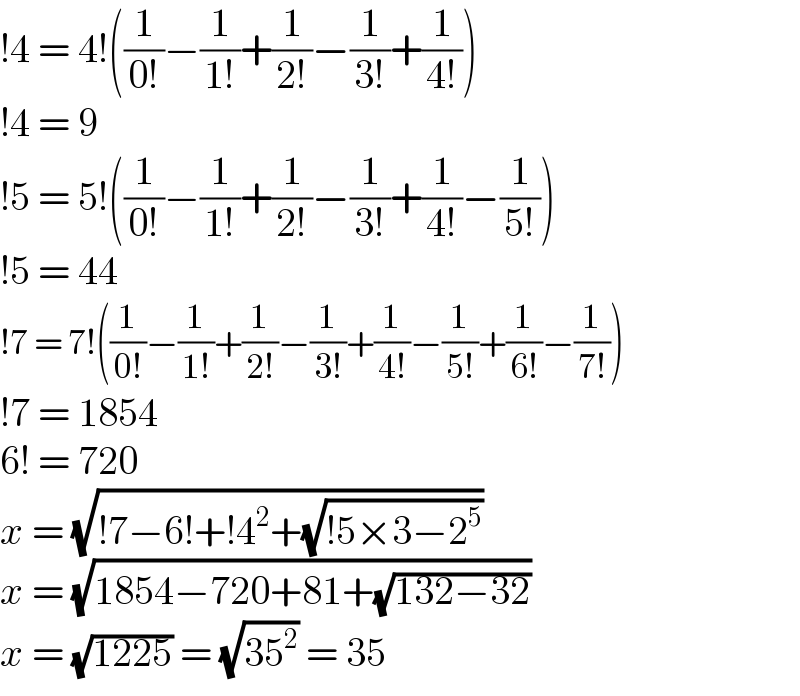
$$!\mathrm{4}\:=\:\mathrm{4}!\left(\frac{\mathrm{1}}{\mathrm{0}!}−\frac{\mathrm{1}}{\mathrm{1}!}+\frac{\mathrm{1}}{\mathrm{2}!}−\frac{\mathrm{1}}{\mathrm{3}!}+\frac{\mathrm{1}}{\mathrm{4}!}\right) \\ $$$$!\mathrm{4}\:=\:\mathrm{9} \\ $$$$!\mathrm{5}\:=\:\mathrm{5}!\left(\frac{\mathrm{1}}{\mathrm{0}!}−\frac{\mathrm{1}}{\mathrm{1}!}+\frac{\mathrm{1}}{\mathrm{2}!}−\frac{\mathrm{1}}{\mathrm{3}!}+\frac{\mathrm{1}}{\mathrm{4}!}−\frac{\mathrm{1}}{\mathrm{5}!}\right) \\ $$$$!\mathrm{5}\:=\:\mathrm{44} \\ $$$$!\mathrm{7}\:=\:\mathrm{7}!\left(\frac{\mathrm{1}}{\mathrm{0}!}−\frac{\mathrm{1}}{\mathrm{1}!}+\frac{\mathrm{1}}{\mathrm{2}!}−\frac{\mathrm{1}}{\mathrm{3}!}+\frac{\mathrm{1}}{\mathrm{4}!}−\frac{\mathrm{1}}{\mathrm{5}!}+\frac{\mathrm{1}}{\mathrm{6}!}−\frac{\mathrm{1}}{\mathrm{7}!}\right) \\ $$$$!\mathrm{7}\:=\:\mathrm{1854} \\ $$$$\mathrm{6}!\:=\:\mathrm{720} \\ $$$${x}\:=\:\sqrt{!\mathrm{7}−\mathrm{6}!+!\mathrm{4}^{\mathrm{2}} +\sqrt{!\mathrm{5}×\mathrm{3}−\mathrm{2}^{\mathrm{5}} }} \\ $$$${x}\:=\:\sqrt{\mathrm{1854}−\mathrm{720}+\mathrm{81}+\sqrt{\mathrm{132}−\mathrm{32}}} \\ $$$${x}\:=\:\sqrt{\mathrm{1225}}\:=\:\sqrt{\mathrm{35}^{\mathrm{2}} }\:=\:\mathrm{35} \\ $$
