Menu Close

Question-145715

Tinku Tara 0 Comments
Pin




Question Number 145715 by Mrsof last updated on 07/Jul/21
Commented by Mrsof last updated on 07/Jul/21
????
$$???? \\ $$
Answered by Dwaipayan Shikari last updated on 07/Jul/21
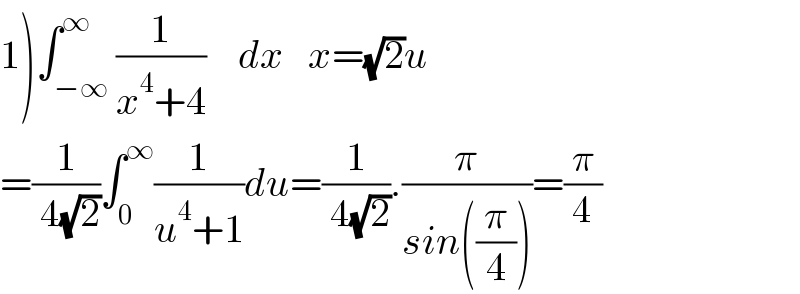
1)∫_(−∞) ^∞ (1/(x^4 +4)) dx x=(√2)u =(1/( 4(√2)))∫_0 ^∞ (1/(u^4 +1))du=(1/( 4(√2))).(π/(sin((π/4))))=(π/4)
$$\left.\mathrm{1}\right)\int_{−\infty} ^{\infty} \frac{\mathrm{1}}{{x}^{\mathrm{4}} +\mathrm{4}}\:\:\:\:{dx}\:\:\:{x}=\sqrt{\mathrm{2}}{u} \\ $$$$=\frac{\mathrm{1}}{\:\mathrm{4}\sqrt{\mathrm{2}}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{{u}^{\mathrm{4}} +\mathrm{1}}{du}=\frac{\mathrm{1}}{\:\mathrm{4}\sqrt{\mathrm{2}}}.\frac{\pi}{{sin}\left(\frac{\pi}{\mathrm{4}}\right)}=\frac{\pi}{\mathrm{4}} \\ $$
Answered by Dwaipayan Shikari last updated on 07/Jul/21
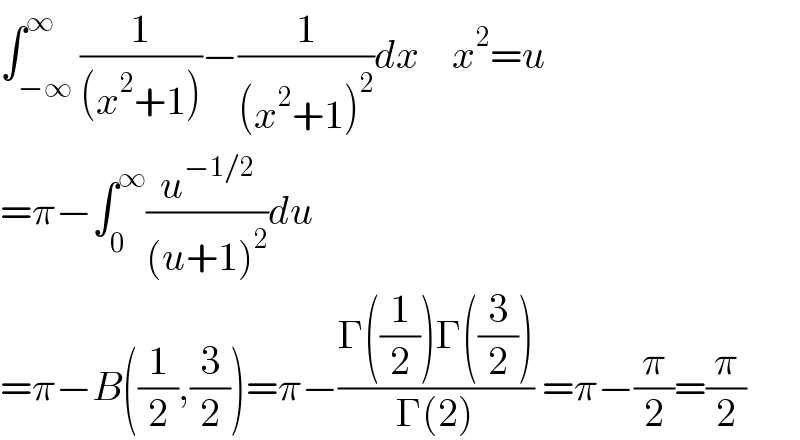
∫_(−∞) ^∞ (1/((x^2 +1)))−(1/((x^2 +1)^2 ))dx x^2 =u =π−∫_0 ^∞ (u^(−1/2) /((u+1)^2 ))du =π−B((1/2),(3/2))=π−((Γ((1/2))Γ((3/2)))/(Γ(2))) =π−(π/2)=(π/2)
$$\int_{−\infty} ^{\infty} \frac{\mathrm{1}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)}−\frac{\mathrm{1}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dx}\:\:\:\:{x}^{\mathrm{2}} ={u} \\ $$$$=\pi−\int_{\mathrm{0}} ^{\infty} \frac{{u}^{−\mathrm{1}/\mathrm{2}} }{\left({u}+\mathrm{1}\right)^{\mathrm{2}} }{du}\:\: \\ $$$$=\pi−{B}\left(\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{3}}{\mathrm{2}}\right)=\pi−\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)}{\Gamma\left(\mathrm{2}\right)}\:=\pi−\frac{\pi}{\mathrm{2}}=\frac{\pi}{\mathrm{2}} \\ $$
Answered by mathmax by abdo last updated on 07/Jul/21
2)∫_(−∞) ^(+∞) (x^2 /((x^2 +1)^2 ))dx =∫_(−∞) ^(+∞) ((x^2 +1−1)/((x^2 +1)^2 ))dx=∫_(−∞) ^(+∞) (dx/(x^2 +1))−∫_(−∞) ^(+∞) (dx/((x^2 +1)^2 )) ∫_(−∞) ^(+∞) (dx/(x^2 +1))=[arctanx]_(−∞) ^(+∞) =π ∫_(−∞) ^(+∞) (dx/((1+x^2 )^2 ))=_(x=tanθ) ∫_(−(π/2)) ^(π/2) (((1+tan^2 θ))/((1+tan^2 θ)^2 ))dθ=∫_(−(π/2)) ^(π/2) (dθ/(1+tan^2 θ)) =2∫_0 ^(π/2) cos^2 θ dθ =∫_0 ^(π/2) (1+cos(2θ))dθ =(π/2) +[(1/2)sin(2θ)]_0 ^(π/2) =(π/2) ⇒∫_(−∞) ^(+∞) (x^2 /((x^2 +1)^2 ))=π−(π/2)=(π/2)
$$\left.\mathrm{2}\right)\int_{−\infty} ^{+\infty} \:\frac{\mathrm{x}^{\mathrm{2}} }{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}\:=\int_{−\infty} ^{+\infty} \:\frac{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}−\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}=\int_{−\infty} ^{+\infty} \:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}−\int_{−\infty} ^{+\infty} \:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\int_{−\infty} ^{+\infty} \:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}=\left[\mathrm{arctanx}\right]_{−\infty} ^{+\infty} \:=\pi \\ $$$$\int_{−\infty} ^{+\infty} \:\frac{\mathrm{dx}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }=_{\mathrm{x}=\mathrm{tan}\theta} \:\:\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta\right)}{\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta\right)^{\mathrm{2}} }\mathrm{d}\theta=\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{d}\theta}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{cos}^{\mathrm{2}} \theta\:\mathrm{d}\theta\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\left(\mathrm{1}+\mathrm{cos}\left(\mathrm{2}\theta\right)\right)\mathrm{d}\theta\:=\frac{\pi}{\mathrm{2}}\:+\left[\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\left(\mathrm{2}\theta\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:=\frac{\pi}{\mathrm{2}} \\ $$$$\Rightarrow\int_{−\infty} ^{+\infty} \:\frac{\mathrm{x}^{\mathrm{2}} }{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }=\pi−\frac{\pi}{\mathrm{2}}=\frac{\pi}{\mathrm{2}} \\ $$
Answered by mathmax by abdo last updated on 07/Jul/21
1)Υ=∫_(−∞) ^(+∞) (dx/(x^4 +4)) ⇒Ψ=_(x=(√2)t) ∫_(−∞) ^(+∞) (((√2)dt)/(4(1+t^4 ))) =((√2)/4)∫_(−∞) ^(+∞) (dt/(t^4 +1)) let ϕ(z)=(1/(z^4 +1)) ⇒ϕ(z)=(1/((z^2 −i)(z^2 +i))) =(1/((z−e^((iπ)/4) )(z+e^((iπ)/4) )(z−e^(−((iπ)/4)) )(z+e^((iπ)/4) ))) so the poles are +^− e^((iπ)/4) and +^− e^(−((iπ)/4)) ∫_R ϕ(z)dz=2iπ{Res(ϕ,e^((iπ)/4) ) +Res(ϕ,−e^(−((iπ)/4)) )} Res(ϕ,e^((iπ)/4) )=(1/(2e^((iπ)/4) (2i)))=(1/(4i))e^(−((iπ)/4)) Res(ϕ,−e^(−((iπ)/4)) )=(1/((−2e^(−((iπ)/4)) )(−2i)))=(1/(4i))e^((iπ)/4) ⇒ ∫_R ϕ(z)dz=2iπ{(1/(4i))e^(−((iπ)/4)) +(1/(4i))e^((iπ)/4) }=(π/2)(2cos((π/4)))=(π/( (√2))) ⇒ Ψ=((√2)/4)×(π/( (√2)))⇒Ψ=(π/4)
$$\left.\mathrm{1}\right)\Upsilon=\int_{−\infty} ^{+\infty} \:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{4}} \:+\mathrm{4}}\:\Rightarrow\Psi=_{\mathrm{x}=\sqrt{\mathrm{2}}\mathrm{t}} \:\:\int_{−\infty} ^{+\infty} \:\frac{\sqrt{\mathrm{2}}\mathrm{dt}}{\mathrm{4}\left(\mathrm{1}+\mathrm{t}^{\mathrm{4}} \right)} \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\int_{−\infty} ^{+\infty} \:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{4}} \:+\mathrm{1}}\:\mathrm{let}\:\varphi\left(\mathrm{z}\right)=\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{4}} \:+\mathrm{1}}\:\Rightarrow\varphi\left(\mathrm{z}\right)=\frac{\mathrm{1}}{\left(\mathrm{z}^{\mathrm{2}} −\mathrm{i}\right)\left(\mathrm{z}^{\mathrm{2}} +\mathrm{i}\right)} \\ $$$$=\frac{\mathrm{1}}{\left(\mathrm{z}−\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)\left(\mathrm{z}+\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)\left(\mathrm{z}−\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)\left(\mathrm{z}+\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)}\:\mathrm{so}\:\mathrm{the}\:\mathrm{poles}\:\mathrm{are}\:\overset{−} {+}\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} \:\mathrm{and}\:\overset{−} {+}\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \\ $$$$\int_{\mathrm{R}} \varphi\left(\mathrm{z}\right)\mathrm{dz}=\mathrm{2i}\pi\left\{\mathrm{Res}\left(\varphi,\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)\:+\mathrm{Res}\left(\varphi,−\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)\right\} \\ $$$$\mathrm{Res}\left(\varphi,\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)=\frac{\mathrm{1}}{\mathrm{2e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} \left(\mathrm{2i}\right)}=\frac{\mathrm{1}}{\mathrm{4i}}\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \\ $$$$\mathrm{Res}\left(\varphi,−\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)=\frac{\mathrm{1}}{\left(−\mathrm{2e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)\left(−\mathrm{2i}\right)}=\frac{\mathrm{1}}{\mathrm{4i}}\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} \:\Rightarrow \\ $$$$\int_{\mathrm{R}} \varphi\left(\mathrm{z}\right)\mathrm{dz}=\mathrm{2i}\pi\left\{\frac{\mathrm{1}}{\mathrm{4i}}\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \:+\frac{\mathrm{1}}{\mathrm{4i}}\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} \right\}=\frac{\pi}{\mathrm{2}}\left(\mathrm{2cos}\left(\frac{\pi}{\mathrm{4}}\right)\right)=\frac{\pi}{\:\sqrt{\mathrm{2}}}\:\Rightarrow \\ $$$$\Psi=\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}×\frac{\pi}{\:\sqrt{\mathrm{2}}}\Rightarrow\Psi=\frac{\pi}{\mathrm{4}} \\ $$
Commented by mathmax by abdo last updated on 07/Jul/21
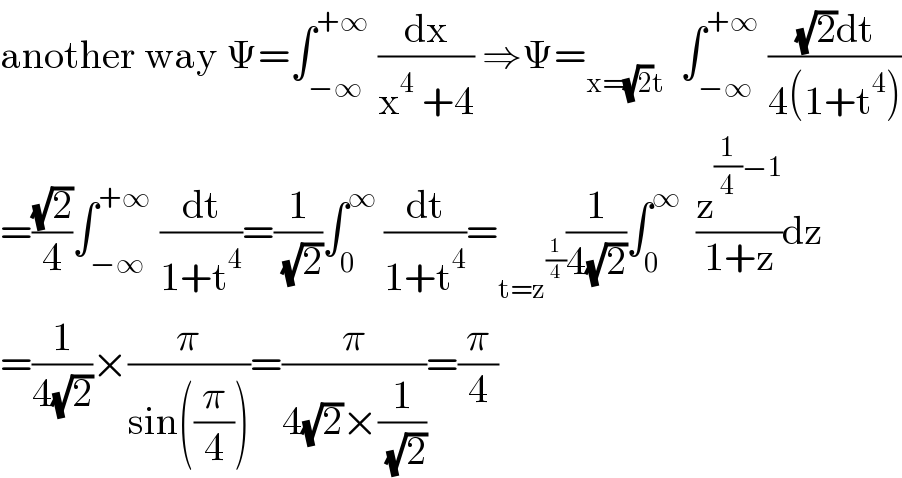
another way Ψ=∫_(−∞) ^(+∞) (dx/(x^4 +4)) ⇒Ψ=_(x=(√2)t) ∫_(−∞) ^(+∞) (((√2)dt)/(4(1+t^4 ))) =((√2)/4)∫_(−∞) ^(+∞) (dt/(1+t^4 ))=(1/( (√2)))∫_0 ^∞ (dt/(1+t^4 ))=_(t=z^(1/4) ) (1/(4(√2)))∫_0 ^∞ (z^((1/4)−1) /(1+z))dz =(1/(4(√2)))×(π/(sin((π/4))))=(π/(4(√2)×(1/( (√2)))))=(π/4)
$$\mathrm{another}\:\mathrm{way}\:\Psi=\int_{−\infty} ^{+\infty} \:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{4}} \:+\mathrm{4}}\:\Rightarrow\Psi=_{\mathrm{x}=\sqrt{\mathrm{2}}\mathrm{t}} \:\:\int_{−\infty} ^{+\infty} \:\frac{\sqrt{\mathrm{2}}\mathrm{dt}}{\mathrm{4}\left(\mathrm{1}+\mathrm{t}^{\mathrm{4}} \right)} \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\int_{−\infty} ^{+\infty} \:\frac{\mathrm{dt}}{\mathrm{1}+\mathrm{t}^{\mathrm{4}} }=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{dt}}{\mathrm{1}+\mathrm{t}^{\mathrm{4}} }=_{\mathrm{t}=\mathrm{z}^{\frac{\mathrm{1}}{\mathrm{4}}} } \frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{z}^{\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{1}} }{\mathrm{1}+\mathrm{z}}\mathrm{dz} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}×\frac{\pi}{\mathrm{sin}\left(\frac{\pi}{\mathrm{4}}\right)}=\frac{\pi}{\mathrm{4}\sqrt{\mathrm{2}}×\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}}=\frac{\pi}{\mathrm{4}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *