Question-145944

Question Number 145944 by alcohol last updated on 09/Jul/21

Commented by alcohol last updated on 10/Jul/21

$${no}\:{body}? \\ $$

Answered by mathmax by abdo last updated on 10/Jul/21

1) { ((u_0 =−6)),((u_(n+1) =(1/3)(u_n −2v_n ) and { ((v_0 =1)),((v_(n+1) =(1/2)(u_n +3v_n ))) :})) :} w_n =u_n +v_n (w_(n+1) /w_n )=((u_(n+1) +v_(n+1) )/(u_n +v_n ))=(((1/3)(u_n −2v_n )+(1/2)(u_n +3v_n ))/(u_n +v_n )) =(((5/6)u_n +(−(2/3)+(3/2))v_n )/(u_n +v_n ))=(5/6)×((u_n +v_n )/(u_n +v_n ))=(5/6) ⇒ w_n is geometric with q=(5/6) w_n =w_0 q^n and w0=u_0 +v_0 =−5 ⇒w_n =−5((5/6))^n 2) we have ∣(5/6)∣<1 ⇒lim_(n→∞) w_n =0

$$\left.\mathrm{1}\right)\:\:\begin{cases}{\mathrm{u}_{\mathrm{0}} =−\mathrm{6}}\\{\mathrm{u}_{\mathrm{n}+\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{u}_{\mathrm{n}} −\mathrm{2v}_{\mathrm{n}} \right)\:\:\:\mathrm{and}\:\:\:\begin{cases}{\mathrm{v}_{\mathrm{0}} =\mathrm{1}}\\{\mathrm{v}_{\mathrm{n}+\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{u}_{\mathrm{n}} +\mathrm{3v}_{\mathrm{n}} \right)}\end{cases}}\end{cases} \\ $$$$\mathrm{w}_{\mathrm{n}} =\mathrm{u}_{\mathrm{n}} +\mathrm{v}_{\mathrm{n}} \\ $$$$\frac{\mathrm{w}_{\mathrm{n}+\mathrm{1}} }{\mathrm{w}_{\mathrm{n}} }=\frac{\mathrm{u}_{\mathrm{n}+\mathrm{1}} +\mathrm{v}_{\mathrm{n}+\mathrm{1}} }{\mathrm{u}_{\mathrm{n}} +\mathrm{v}_{\mathrm{n}} }=\frac{\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{u}_{\mathrm{n}} −\mathrm{2v}_{\mathrm{n}} \right)+\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{u}_{\mathrm{n}} +\mathrm{3v}_{\mathrm{n}} \right)}{\mathrm{u}_{\mathrm{n}} +\mathrm{v}_{\mathrm{n}} } \\ $$$$=\frac{\frac{\mathrm{5}}{\mathrm{6}}\mathrm{u}_{\mathrm{n}} +\left(−\frac{\mathrm{2}}{\mathrm{3}}+\frac{\mathrm{3}}{\mathrm{2}}\right)\mathrm{v}_{\mathrm{n}} }{\mathrm{u}_{\mathrm{n}} +\mathrm{v}_{\mathrm{n}} }=\frac{\mathrm{5}}{\mathrm{6}}×\frac{\mathrm{u}_{\mathrm{n}} +\mathrm{v}_{\mathrm{n}} }{\mathrm{u}_{\mathrm{n}} +\mathrm{v}_{\mathrm{n}} }=\frac{\mathrm{5}}{\mathrm{6}}\:\Rightarrow \\ $$$$\mathrm{w}_{\mathrm{n}} \mathrm{is}\:\mathrm{geometric}\:\:\mathrm{with}\:\mathrm{q}=\frac{\mathrm{5}}{\mathrm{6}} \\ $$$$\mathrm{w}_{\mathrm{n}} =\mathrm{w}_{\mathrm{0}} \mathrm{q}^{\mathrm{n}} \:\:\:\:\mathrm{and}\:\mathrm{w0}=\mathrm{u}_{\mathrm{0}} +\mathrm{v}_{\mathrm{0}} =−\mathrm{5}\:\Rightarrow\mathrm{w}_{\mathrm{n}} =−\mathrm{5}\left(\frac{\mathrm{5}}{\mathrm{6}}\right)^{\mathrm{n}} \\ $$$$\left.\mathrm{2}\right)\:\mathrm{we}\:\mathrm{have}\:\mid\frac{\mathrm{5}}{\mathrm{6}}\mid<\mathrm{1}\:\Rightarrow\mathrm{lim}_{\mathrm{n}\rightarrow\infty} \mathrm{w}_{\mathrm{n}} =\mathrm{0} \\ $$

Commented by physicstutes last updated on 11/Jul/21

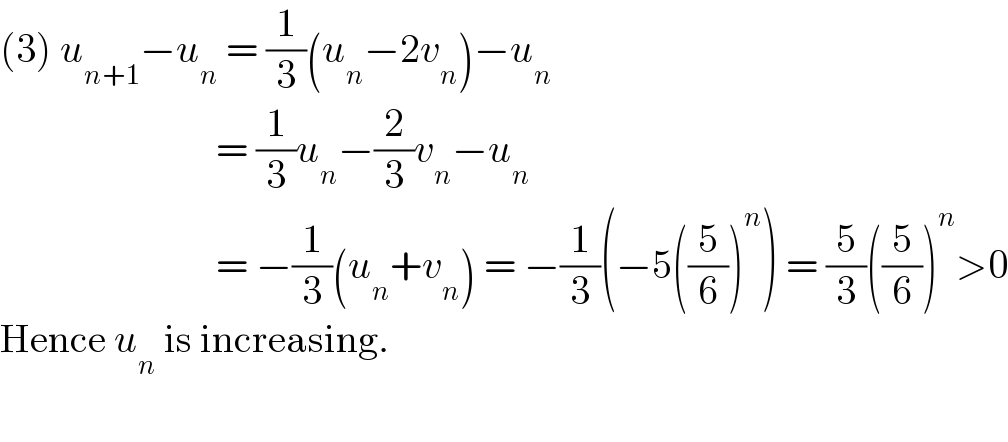
(3) u_(n+1) −u_n = (1/3)(u_n −2v_n )−u_n = (1/3)u_n −(2/3)v_n −u_n = −(1/3)(u_n +v_n ) = −(1/3)(−5((5/6))^n ) = (5/3)((5/6))^n >0 Hence u_n is increasing.

$$\left(\mathrm{3}\right)\:{u}_{{n}+\mathrm{1}} −{u}_{{n}} \:=\:\frac{\mathrm{1}}{\mathrm{3}}\left({u}_{{n}} −\mathrm{2}{v}_{{n}} \right)−{u}_{{n}} \: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{3}}{u}_{{n}} −\frac{\mathrm{2}}{\mathrm{3}}{v}_{{n}} −{u}_{{n}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:−\frac{\mathrm{1}}{\mathrm{3}}\left({u}_{{n}} +{v}_{{n}} \right)\:=\:−\frac{\mathrm{1}}{\mathrm{3}}\left(−\mathrm{5}\left(\frac{\mathrm{5}}{\mathrm{6}}\right)^{{n}} \right)\:=\:\frac{\mathrm{5}}{\mathrm{3}}\left(\frac{\mathrm{5}}{\mathrm{6}}\right)^{{n}} >\mathrm{0} \\ $$$$\mathrm{Hence}\:{u}_{{n}} \:\mathrm{is}\:\mathrm{increasing}. \\ $$$$ \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply