Question Number 146026 by ajfour last updated on 10/Jul/21
Commented by ajfour last updated on 10/Jul/21
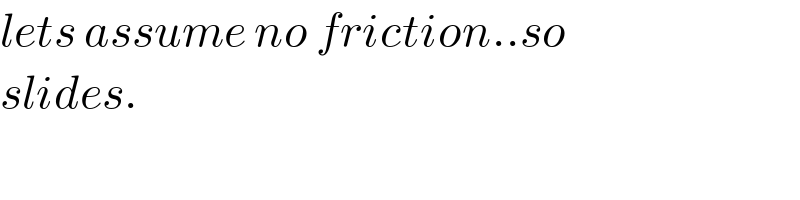
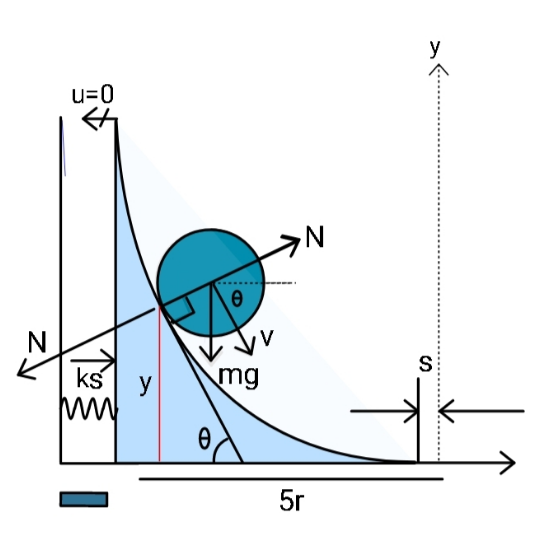
$${lets}\:{assume}\:{no}\:{friction}..{so} \\ $$$${slides}. \\ $$
Commented by ajfour last updated on 10/Jul/21

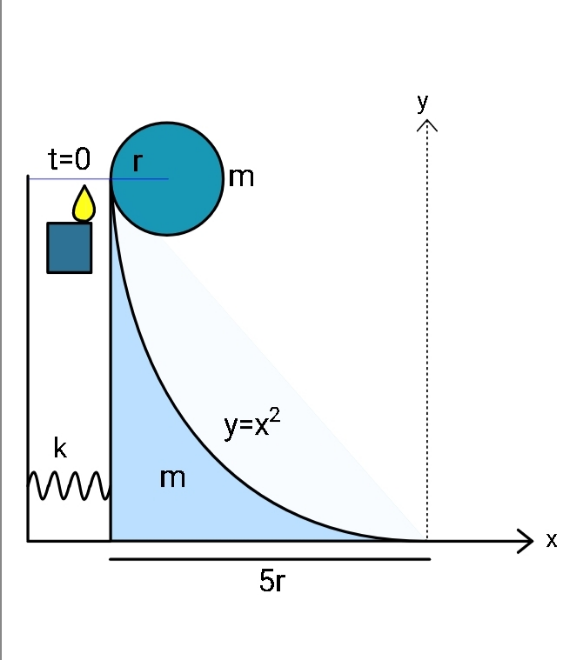
$${A}\:{parabolic}\:{wedge}\:{rests}\:{on}\:{a} \\ $$$${frictionless}\:{ground}.\:{Now}\:{a} \\ $$$${cylinder}\:{of}\:{an}\:{equal}\:{mass}\:{is} \\ $$$${released}\:{onto}\:{the}\:{wedge}-{top}. \\ $$$${Find}\:{maximum}\:{compression} \\ $$$${of}\:{the}\:{spring}\:\left({by}\:{the}\:{time}\:{the}\right. \\ $$$${cylinder}\:{loses}\:{contact}\:{with} \\ $$$${the}\:{curved}\:{surface}\:{the}\:{first} \\ $$$$\left.{time}\right). \\ $$
Commented by mr W last updated on 10/Jul/21
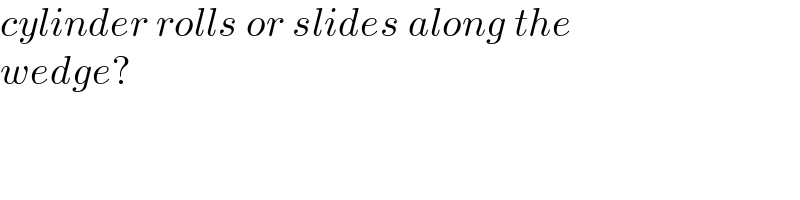
$${cylinder}\:{rolls}\:{or}\:{slides}\:{along}\:{the}\: \\ $$$${wedge}? \\ $$
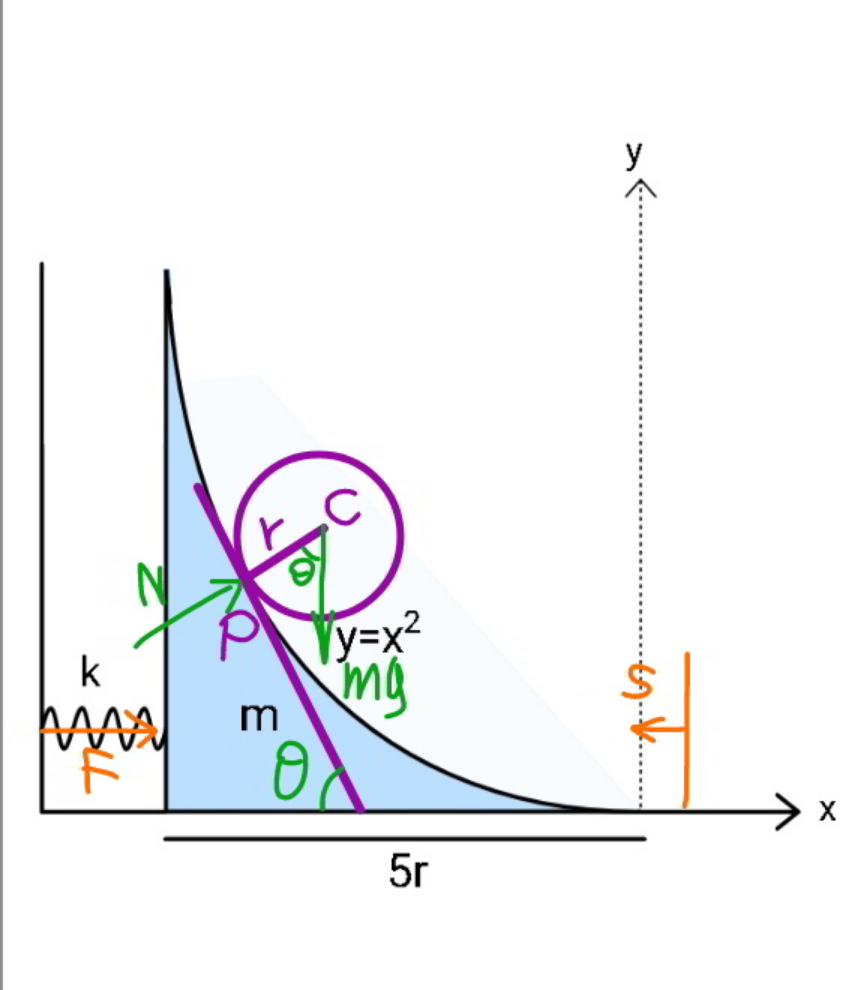
Answered by mr W last updated on 10/Jul/21
Commented by mr W last updated on 11/Jul/21
![at time t displacement of wedge is s P(p,kp^2 ) with k=1 tan θ=2kp U=(ds/dt) u=(dp/dt) x_C =s+p−r sin θ=s+p−((2rkp)/( (√(1+(2kp)^2 )))) y_C =kp^2 +r cos θ=kp^2 +(r/( (√(1+(2kp)^2 )))) v_x =U+[1−((2rk)/( (√(1+(2kp)^2 ))))+((8rk^3 p^2 )/((1+(2kp)^2 )^(3/2) ))]u v_y =2kp[1−((2rk)/((1+(2kp)^2 )^(3/2) ))]u .....](https://www.tinkutara.com/question/Q146175.png)
$${at}\:{time}\:{t} \\ $$$${displacement}\:{of}\:{wedge}\:{is}\:{s} \\ $$$${P}\left({p},{kp}^{\mathrm{2}} \right)\:{with}\:{k}=\mathrm{1} \\ $$$$\mathrm{tan}\:\theta=\mathrm{2}{kp} \\ $$$${U}=\frac{{ds}}{{dt}} \\ $$$${u}=\frac{{dp}}{{dt}} \\ $$$${x}_{{C}} ={s}+{p}−{r}\:\mathrm{sin}\:\theta={s}+{p}−\frac{\mathrm{2}{rkp}}{\:\sqrt{\mathrm{1}+\left(\mathrm{2}{kp}\right)^{\mathrm{2}} }} \\ $$$${y}_{{C}} ={kp}^{\mathrm{2}} +{r}\:\mathrm{cos}\:\theta={kp}^{\mathrm{2}} +\frac{{r}}{\:\sqrt{\mathrm{1}+\left(\mathrm{2}{kp}\right)^{\mathrm{2}} }} \\ $$$${v}_{{x}} ={U}+\left[\mathrm{1}−\frac{\mathrm{2}{rk}}{\:\sqrt{\mathrm{1}+\left(\mathrm{2}{kp}\right)^{\mathrm{2}} }}+\frac{\mathrm{8}{rk}^{\mathrm{3}} {p}^{\mathrm{2}} }{\left(\mathrm{1}+\left(\mathrm{2}{kp}\right)^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} }\right]{u} \\ $$$${v}_{{y}} =\mathrm{2}{kp}\left[\mathrm{1}−\frac{\mathrm{2}{rk}}{\left(\mathrm{1}+\left(\mathrm{2}{kp}\right)^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} }\right]{u} \\ $$$$….. \\ $$
Answered by ajfour last updated on 10/Jul/21