Question Number 146043 by liberty last updated on 10/Jul/21
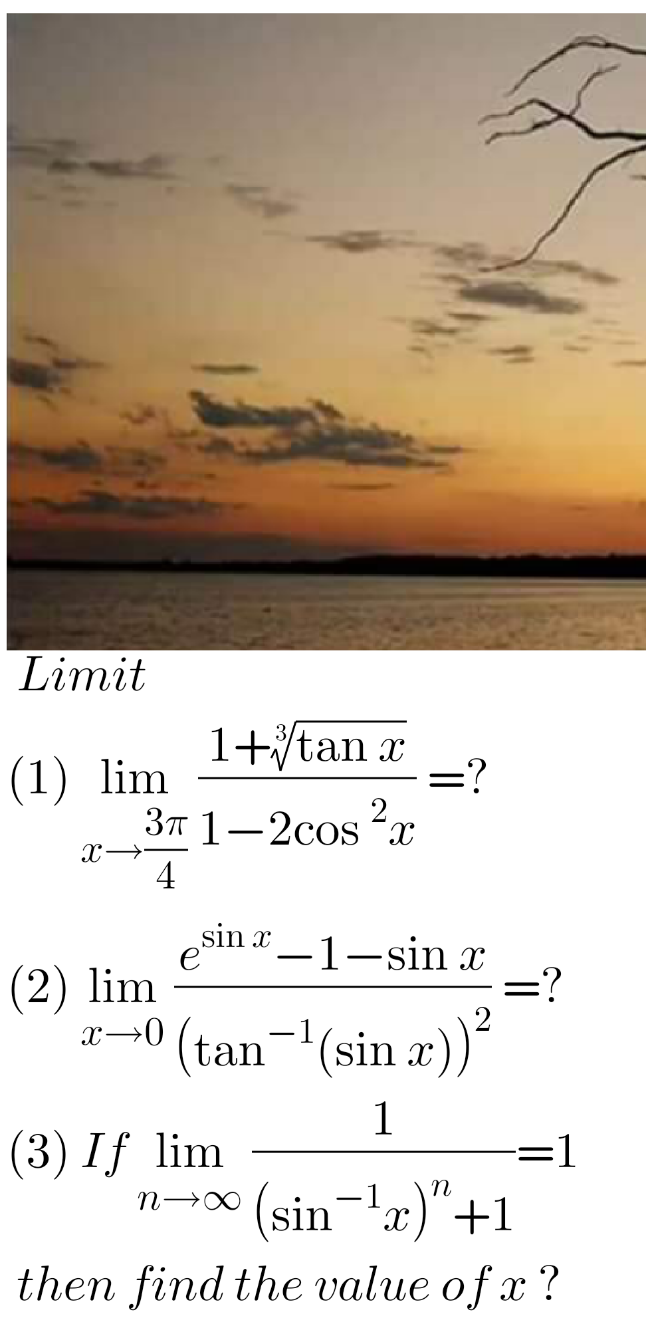
Answered by iloveisrael last updated on 10/Jul/21
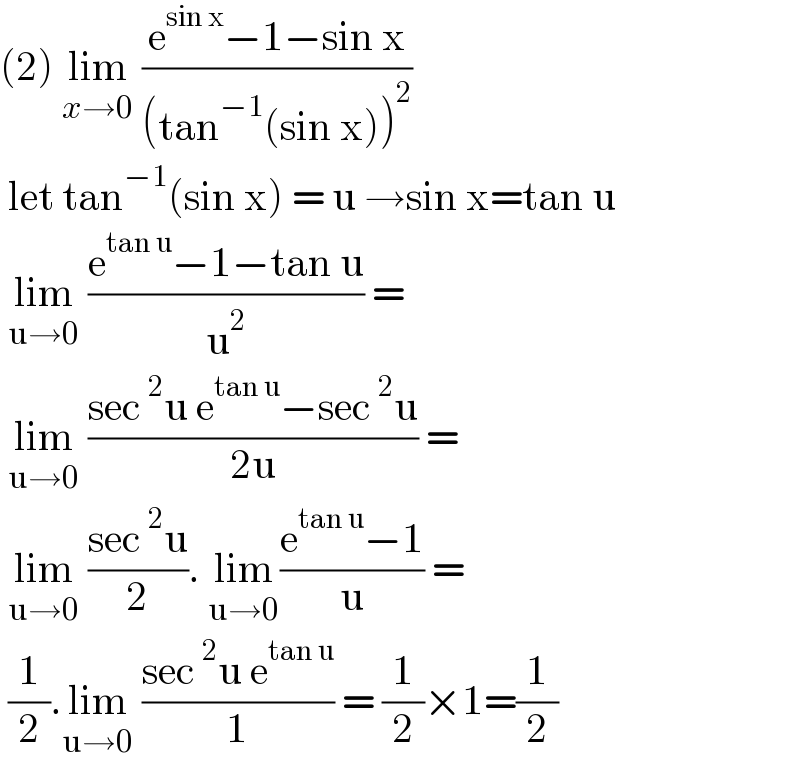
$$\left(\mathrm{2}\right)\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{e}^{\mathrm{sin}\:\mathrm{x}} −\mathrm{1}−\mathrm{sin}\:\mathrm{x}}{\left(\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{sin}\:\mathrm{x}\right)\right)^{\mathrm{2}} } \\ $$$$\:\mathrm{let}\:\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{sin}\:\mathrm{x}\right)\:=\:\mathrm{u}\:\rightarrow\mathrm{sin}\:\mathrm{x}=\mathrm{tan}\:\mathrm{u}\: \\ $$$$\:\underset{\mathrm{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{e}^{\mathrm{tan}\:\mathrm{u}} −\mathrm{1}−\mathrm{tan}\:\mathrm{u}}{\mathrm{u}^{\mathrm{2}} }\:= \\ $$$$\:\underset{\mathrm{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sec}\:^{\mathrm{2}} \mathrm{u}\:\mathrm{e}^{\mathrm{tan}\:\mathrm{u}} −\mathrm{sec}\:^{\mathrm{2}} \mathrm{u}}{\mathrm{2u}}\:= \\ $$$$\:\underset{\mathrm{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sec}\:^{\mathrm{2}} \mathrm{u}}{\mathrm{2}}.\:\underset{\mathrm{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{e}^{\mathrm{tan}\:\mathrm{u}} −\mathrm{1}}{\mathrm{u}}\:= \\ $$$$\:\frac{\mathrm{1}}{\mathrm{2}}.\underset{\mathrm{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sec}\:^{\mathrm{2}} \mathrm{u}\:\mathrm{e}^{\mathrm{tan}\:\mathrm{u}} }{\mathrm{1}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{1}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Answered by iloveisrael last updated on 10/Jul/21

$$\left(\mathrm{1}\right)\:\underset{{x}\rightarrow\frac{\mathrm{3}\pi}{\mathrm{4}}} {\mathrm{lim}}\:\frac{\mathrm{1}+\sqrt[{\mathrm{3}}]{\mathrm{tan}\:\mathrm{x}}}{\mathrm{1}−\mathrm{2cos}\:^{\mathrm{2}} \mathrm{x}}\: \\ $$$$\:\:\:=\:\underset{{x}\rightarrow\frac{\mathrm{3}\pi}{\mathrm{4}}} {\mathrm{lim}}\:\frac{\mathrm{1}+\mathrm{tan}\:\mathrm{x}}{\mathrm{1}−\mathrm{2cos}\:^{\mathrm{2}} \mathrm{x}}\:.\underset{{x}\rightarrow\frac{\mathrm{3}\pi}{\mathrm{4}}} {\mathrm{lim}}\:\:\frac{\mathrm{1}}{\mathrm{1}+\sqrt[{\mathrm{3}}]{\mathrm{tan}\:^{\mathrm{2}} \mathrm{x}}−\sqrt[{\mathrm{3}}]{\mathrm{tan}\:\mathrm{x}}}\: \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{3}}×\underset{{x}\rightarrow\frac{\mathrm{3}\pi}{\mathrm{4}}} {\mathrm{lim}}\:\frac{\mathrm{cos}\:\mathrm{x}+\mathrm{sin}\:\mathrm{x}}{\mathrm{cos}\:\mathrm{x}\left(−\mathrm{cos}\:\mathrm{2x}\right)} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{3}}×\underset{{x}\rightarrow\frac{\mathrm{3}\pi}{\mathrm{4}}} {\mathrm{lim}}\:\frac{\mathrm{1}}{\mathrm{cos}\:\mathrm{x}\left(\mathrm{cos}\:\mathrm{x}−\mathrm{sin}\:\mathrm{x}\right)} \\ $$$$=\:−\frac{\mathrm{1}}{\mathrm{3}}×\frac{\mathrm{1}}{−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left(−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}×\frac{\mathrm{1}}{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}.\frac{\mathrm{2}}{\:\sqrt{\mathrm{2}}}}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$
