Question Number 146183 by tabata last updated on 11/Jul/21
Commented by tabata last updated on 11/Jul/21

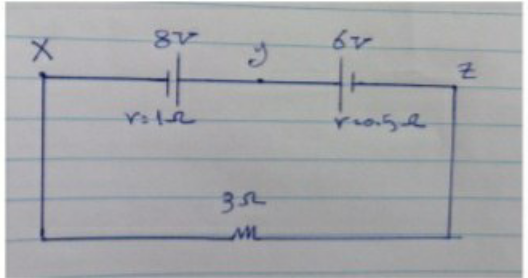
$${in}\:{the}\:{adjacent}\:{figure}\:,{calculate}\: \\ $$$$ \\ $$$$\left(\mathrm{1}\right)\:{the}\:{intensity}\:{of}\:{the}\:{current}\:{passing}\:{throuph}\:{the}\:{circuit} \\ $$$$ \\ $$$$\left(\mathrm{2}\right){the}\:{potential}\:{difference}\:{between}\:{the}\:{two}\:{points}\:{x},{y} \\ $$$$ \\ $$$$\left(\mathrm{3}\right){the}\:{potential}\:{difference}\:{between}\:{the}\:{two}\:{points}\:{y},{x} \\ $$
Answered by Olaf_Thorendsen last updated on 11/Jul/21
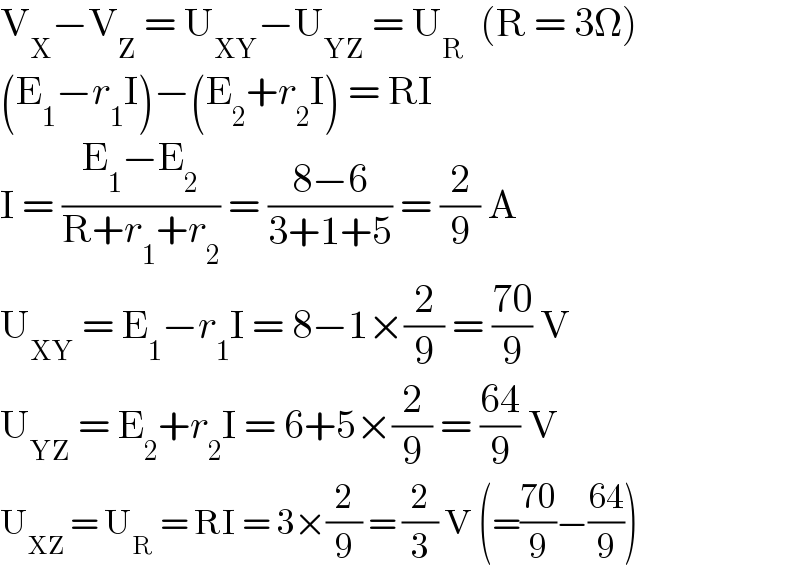
$$\mathrm{V}_{\mathrm{X}} −\mathrm{V}_{\mathrm{Z}} \:=\:\mathrm{U}_{\mathrm{XY}} −\mathrm{U}_{\mathrm{YZ}} \:=\:\mathrm{U}_{\mathrm{R}} \:\:\left(\mathrm{R}\:=\:\mathrm{3}\Omega\right) \\ $$$$\left(\mathrm{E}_{\mathrm{1}} −{r}_{\mathrm{1}} \mathrm{I}\right)−\left(\mathrm{E}_{\mathrm{2}} +{r}_{\mathrm{2}} \mathrm{I}\right)\:=\:\mathrm{RI} \\ $$$$\mathrm{I}\:=\:\frac{\mathrm{E}_{\mathrm{1}} −\mathrm{E}_{\mathrm{2}} }{\mathrm{R}+{r}_{\mathrm{1}} +{r}_{\mathrm{2}} }\:=\:\frac{\mathrm{8}−\mathrm{6}}{\mathrm{3}+\mathrm{1}+\mathrm{5}}\:=\:\frac{\mathrm{2}}{\mathrm{9}}\:\mathrm{A} \\ $$$$\mathrm{U}_{\mathrm{XY}} \:=\:\mathrm{E}_{\mathrm{1}} −{r}_{\mathrm{1}} \mathrm{I}\:=\:\mathrm{8}−\mathrm{1}×\frac{\mathrm{2}}{\mathrm{9}}\:=\:\frac{\mathrm{70}}{\mathrm{9}}\:\mathrm{V} \\ $$$$\mathrm{U}_{\mathrm{YZ}} \:=\:\mathrm{E}_{\mathrm{2}} +{r}_{\mathrm{2}} \mathrm{I}\:=\:\mathrm{6}+\mathrm{5}×\frac{\mathrm{2}}{\mathrm{9}}\:=\:\frac{\mathrm{64}}{\mathrm{9}}\:\mathrm{V} \\ $$$$\mathrm{U}_{\mathrm{XZ}} \:=\:\mathrm{U}_{\mathrm{R}} \:=\:\mathrm{RI}\:=\:\mathrm{3}×\frac{\mathrm{2}}{\mathrm{9}}\:=\:\frac{\mathrm{2}}{\mathrm{3}}\:\mathrm{V}\:\left(=\frac{\mathrm{70}}{\mathrm{9}}−\frac{\mathrm{64}}{\mathrm{9}}\right) \\ $$
Commented by Olaf_Thorendsen last updated on 11/Jul/21
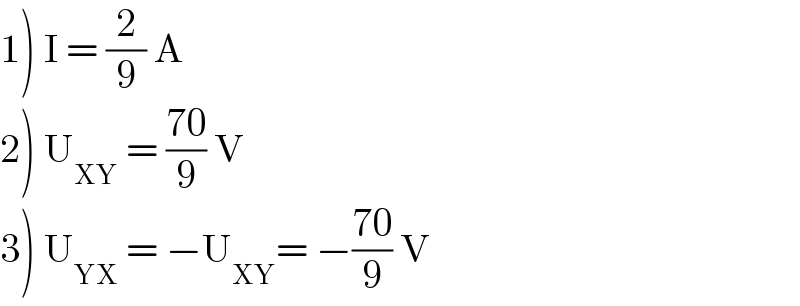
$$\left.\mathrm{1}\right)\:\mathrm{I}\:=\:\frac{\mathrm{2}}{\mathrm{9}}\:\mathrm{A} \\ $$$$\left.\mathrm{2}\right)\:\mathrm{U}_{\mathrm{XY}} \:=\:\frac{\mathrm{70}}{\mathrm{9}}\:\mathrm{V} \\ $$$$\left.\mathrm{3}\right)\:\mathrm{U}_{\mathrm{YX}} \:=\:−\mathrm{U}_{\mathrm{XY}} =\:−\frac{\mathrm{70}}{\mathrm{9}}\:\mathrm{V} \\ $$
