Menu Close

Question-146300

Tinku Tara 0 Comments
Pin




Question Number 146300 by akolade last updated on 12/Jul/21
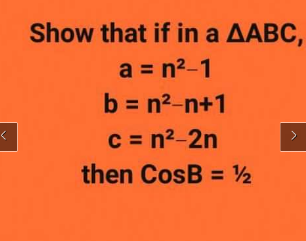
Answered by nimnim last updated on 12/Jul/21
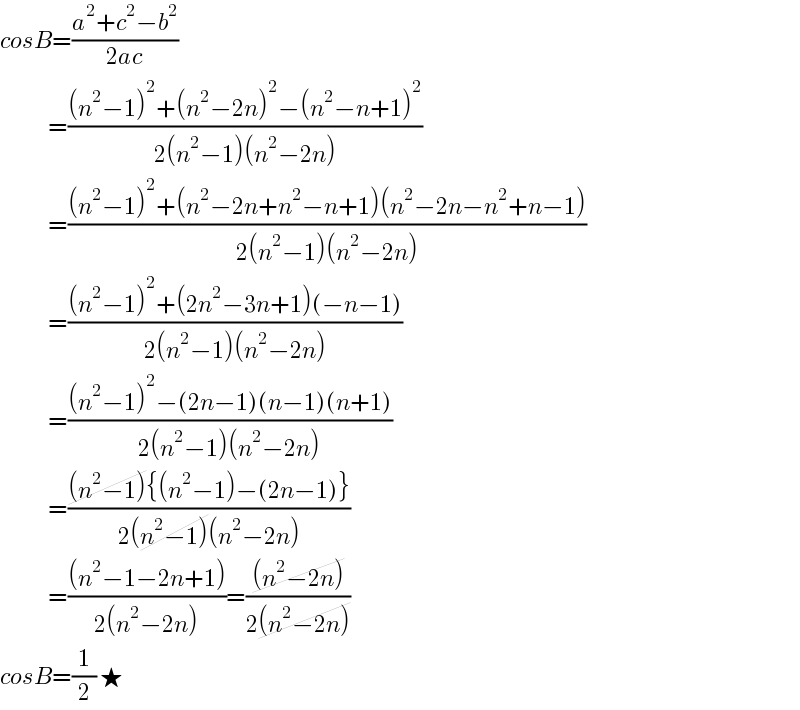
cosB=((a^2 +c^2 −b^2 )/(2ac)) =(((n^2 −1)^2 +(n^2 −2n)^2 −(n^2 −n+1)^2 )/(2(n^2 −1)(n^2 −2n))) =(((n^2 −1)^2 +(n^2 −2n+n^2 −n+1)(n^2 −2n−n^2 +n−1))/(2(n^2 −1)(n^2 −2n))) =(((n^2 −1)^2 +(2n^2 −3n+1)(−n−1))/(2(n^2 −1)(n^2 −2n))) =(((n^2 −1)^2 −(2n−1)(n−1)(n+1))/(2(n^2 −1)(n^2 −2n))) =(((n^2 −1){(n^2 −1)−(2n−1)})/(2(n^2 −1)(n^2 −2n))) =(((n^2 −1−2n+1))/(2(n^2 −2n)))=(((n^2 −2n))/(2(n^2 −2n))) cosB=(1/2) ★
$${cosB}=\frac{{a}^{\mathrm{2}} +{c}^{\mathrm{2}} −{b}^{\mathrm{2}} }{\mathrm{2}{ac}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\left({n}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} +\left({n}^{\mathrm{2}} −\mathrm{2}{n}\right)^{\mathrm{2}} −\left({n}^{\mathrm{2}} −{n}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{2}\left({n}^{\mathrm{2}} −\mathrm{1}\right)\left({n}^{\mathrm{2}} −\mathrm{2}{n}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\left({n}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} +\left({n}^{\mathrm{2}} −\mathrm{2}{n}+{n}^{\mathrm{2}} −{n}+\mathrm{1}\right)\left({n}^{\mathrm{2}} −\mathrm{2}{n}−{n}^{\mathrm{2}} +{n}−\mathrm{1}\right)}{\mathrm{2}\left({n}^{\mathrm{2}} −\mathrm{1}\right)\left({n}^{\mathrm{2}} −\mathrm{2}{n}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\left({n}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} +\left(\mathrm{2}{n}^{\mathrm{2}} −\mathrm{3}{n}+\mathrm{1}\right)\left(−{n}−\mathrm{1}\right)}{\mathrm{2}\left({n}^{\mathrm{2}} −\mathrm{1}\right)\left({n}^{\mathrm{2}} −\mathrm{2}{n}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\left({n}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} −\left(\mathrm{2}{n}−\mathrm{1}\right)\left({n}−\mathrm{1}\right)\left({n}+\mathrm{1}\right)}{\mathrm{2}\left({n}^{\mathrm{2}} −\mathrm{1}\right)\left({n}^{\mathrm{2}} −\mathrm{2}{n}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\cancel{\left({n}^{\mathrm{2}} −\mathrm{1}\right)}\left\{\left({n}^{\mathrm{2}} −\mathrm{1}\right)−\left(\mathrm{2}{n}−\mathrm{1}\right)\right\}}{\mathrm{2}\left(\cancel{{n}^{\mathrm{2}} −\mathrm{1}\right)}\left({n}^{\mathrm{2}} −\mathrm{2}{n}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\left({n}^{\mathrm{2}} −\mathrm{1}−\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{2}\left({n}^{\mathrm{2}} −\mathrm{2}{n}\right)}=\frac{\cancel{\left({n}^{\mathrm{2}} −\mathrm{2}{n}\right)}}{\mathrm{2}\cancel{\left({n}^{\mathrm{2}} −\mathrm{2}{n}\right)}} \\ $$$${cosB}=\frac{\mathrm{1}}{\mathrm{2}}\:\bigstar \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *