Question Number 146315 by mnjuly1970 last updated on 12/Jul/21
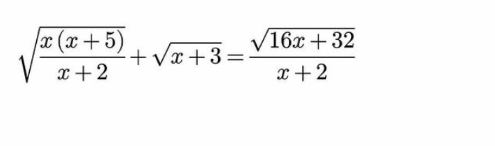
Answered by Olaf_Thorendsen last updated on 13/Jul/21
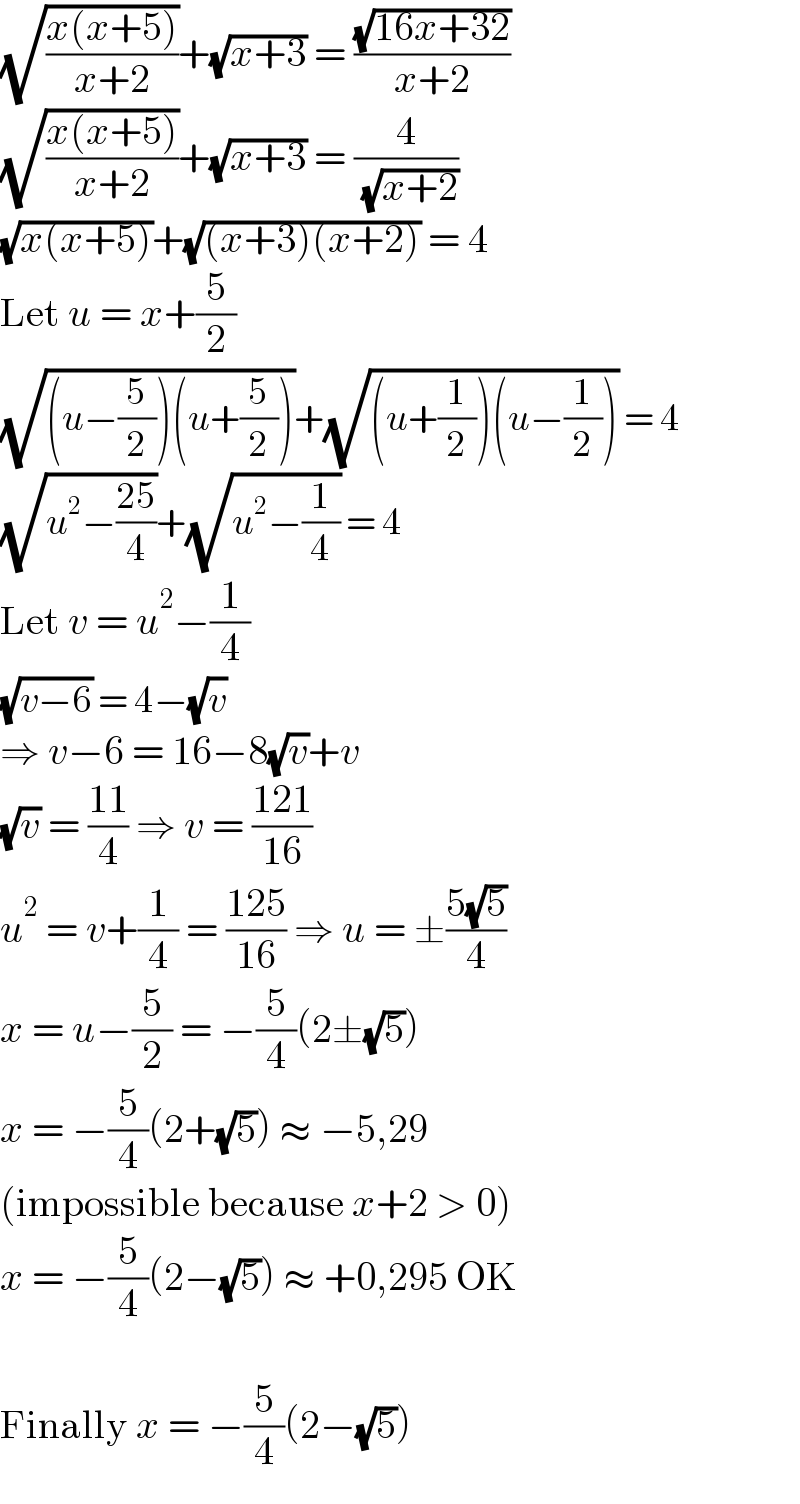
$$\sqrt{\frac{{x}\left({x}+\mathrm{5}\right)}{{x}+\mathrm{2}}}+\sqrt{{x}+\mathrm{3}}\:=\:\frac{\sqrt{\mathrm{16}{x}+\mathrm{32}}}{{x}+\mathrm{2}} \\ $$$$\sqrt{\frac{{x}\left({x}+\mathrm{5}\right)}{{x}+\mathrm{2}}}+\sqrt{{x}+\mathrm{3}}\:=\:\frac{\mathrm{4}}{\:\sqrt{{x}+\mathrm{2}}} \\ $$$$\sqrt{{x}\left({x}+\mathrm{5}\right)}+\sqrt{\left({x}+\mathrm{3}\right)\left({x}+\mathrm{2}\right)}\:=\:\mathrm{4} \\ $$$$\mathrm{Let}\:{u}\:=\:{x}+\frac{\mathrm{5}}{\mathrm{2}} \\ $$$$\sqrt{\left({u}−\frac{\mathrm{5}}{\mathrm{2}}\right)\left({u}+\frac{\mathrm{5}}{\mathrm{2}}\right)}+\sqrt{\left({u}+\frac{\mathrm{1}}{\mathrm{2}}\right)\left({u}−\frac{\mathrm{1}}{\mathrm{2}}\right)}\:=\:\mathrm{4} \\ $$$$\sqrt{{u}^{\mathrm{2}} −\frac{\mathrm{25}}{\mathrm{4}}}+\sqrt{{u}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}}\:=\:\mathrm{4} \\ $$$$\mathrm{Let}\:{v}\:=\:{u}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\sqrt{{v}−\mathrm{6}}\:=\:\mathrm{4}−\sqrt{{v}} \\ $$$$\Rightarrow\:{v}−\mathrm{6}\:=\:\mathrm{16}−\mathrm{8}\sqrt{{v}}+{v} \\ $$$$\sqrt{{v}}\:=\:\frac{\mathrm{11}}{\mathrm{4}}\:\Rightarrow\:{v}\:=\:\frac{\mathrm{121}}{\mathrm{16}} \\ $$$${u}^{\mathrm{2}} \:=\:{v}+\frac{\mathrm{1}}{\mathrm{4}}\:=\:\frac{\mathrm{125}}{\mathrm{16}}\:\Rightarrow\:{u}\:=\:\pm\frac{\mathrm{5}\sqrt{\mathrm{5}}}{\mathrm{4}} \\ $$$${x}\:=\:{u}−\frac{\mathrm{5}}{\mathrm{2}}\:=\:−\frac{\mathrm{5}}{\mathrm{4}}\left(\mathrm{2}\pm\sqrt{\mathrm{5}}\right) \\ $$$${x}\:=\:−\frac{\mathrm{5}}{\mathrm{4}}\left(\mathrm{2}+\sqrt{\mathrm{5}}\right)\:\approx\:−\mathrm{5},\mathrm{29} \\ $$$$\left(\mathrm{impossible}\:\mathrm{because}\:{x}+\mathrm{2}\:>\:\mathrm{0}\right) \\ $$$${x}\:=\:−\frac{\mathrm{5}}{\mathrm{4}}\left(\mathrm{2}−\sqrt{\mathrm{5}}\right)\:\approx\:+\mathrm{0},\mathrm{295}\:\mathrm{OK} \\ $$$$ \\ $$$$\mathrm{Finally}\:{x}\:=\:−\frac{\mathrm{5}}{\mathrm{4}}\left(\mathrm{2}−\sqrt{\mathrm{5}}\right) \\ $$
Commented by mnjuly1970 last updated on 13/Jul/21
$${thank}\:{you}\:{mr}\:{olaf} \\ $$
