Question-146316

Question Number 146316 by mathdanisur last updated on 12/Jul/21

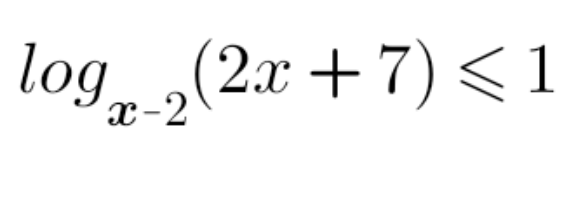
Answered by Ar Brandon last updated on 12/Jul/21

$$\mathrm{log}_{\mathrm{x}−\mathrm{2}} \left(\mathrm{2x}+\mathrm{7}\right)\leqslant\mathrm{1} \\ $$$$\mathrm{Conditions}; \\ $$$$\mathrm{2x}+\mathrm{7}>\mathrm{0}\:\wedge\:\mathrm{1}\neq\mathrm{x}−\mathrm{2}>\mathrm{0}, \\ $$$$\Rightarrow\left(\mathrm{x}>−\frac{\mathrm{7}}{\mathrm{2}}\right)\:\wedge\left(\:\mathrm{0}<\mathrm{x}−\mathrm{2}<\mathrm{1}\cup\mathrm{x}−\mathrm{2}>\mathrm{1}\right) \\ $$$$\Rightarrow\left(\mathrm{x}>−\frac{\mathrm{7}}{\mathrm{2}}\right)\wedge\left(\mathrm{2}<\mathrm{x}<\mathrm{3}\cup\mathrm{x}>\mathrm{3}\right) \\ $$$$\mathrm{Case}\:\mathrm{1}:\:\mathrm{2}<\mathrm{x}<\mathrm{3} \\ $$$$\mathrm{log}_{\mathrm{x}−\mathrm{2}} \left(\mathrm{2x}+\mathrm{7}\right)\leqslant\mathrm{1}\Rightarrow\mathrm{2x}+\mathrm{7}\geqslant\mathrm{x}−\mathrm{2}\Rightarrow\mathrm{x}\geqslant−\mathrm{9} \\ $$$$\Rightarrow\mathrm{x}\in\left(\mathrm{2},\:\mathrm{3}\right)\:\mathrm{by}\:\mathrm{hypothesis}. \\ $$$$\mathrm{Case}\:\mathrm{2}:\:\mathrm{x}>\mathrm{3} \\ $$$$\mathrm{log}_{\mathrm{x}−\mathrm{2}} \left(\mathrm{2x}+\mathrm{7}\right)\leqslant\mathrm{1}\:\Rightarrow\mathrm{2x}+\mathrm{7}\leqslant\mathrm{x}−\mathrm{2}\Rightarrow\mathrm{x}\leqslant−\mathrm{9} \\ $$$$\mathrm{Absurd},\:\mathrm{since}\:\mathrm{x}>\mathrm{3}\:\mathrm{by}\:\mathrm{hypothesis} \\ $$$$\mathrm{Unique}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{2}<\mathrm{x}<\mathrm{3} \\ $$

Commented by mathdanisur last updated on 12/Jul/21

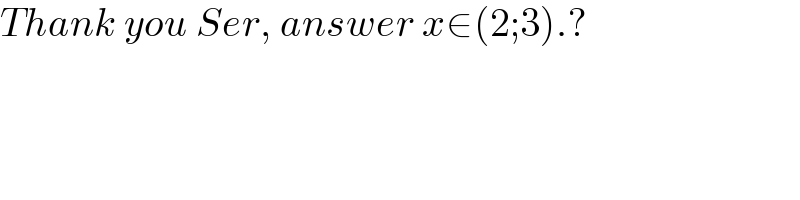
$${Thank}\:{you}\:{Ser},\:{answer}\:{x}\in\left(\mathrm{2};\mathrm{3}\right).? \\ $$

Commented by Ar Brandon last updated on 12/Jul/21

$$\mathrm{Yes} \\ $$$$\left.\mathrm{x}\in\left(\mathrm{2},\:\mathrm{3}\right)\Leftrightarrow\mathrm{2}<\mathrm{x}<\mathrm{3}\:\Leftrightarrow\:\mathrm{x}\in\right]\mathrm{2},\:\mathrm{3}\left[\right. \\ $$

Commented by mathdanisur last updated on 12/Jul/21

$${cool}\:{thanks}\:{Ser} \\ $$

Answered by iloveisrael last updated on 13/Jul/21

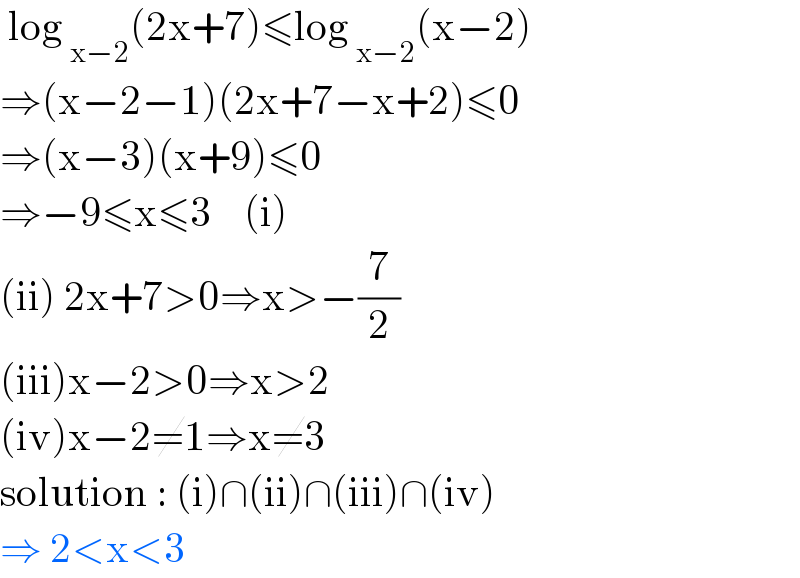
$$\:\mathrm{log}\:_{\mathrm{x}−\mathrm{2}} \left(\mathrm{2x}+\mathrm{7}\right)\leqslant\mathrm{log}\:_{\mathrm{x}−\mathrm{2}} \left(\mathrm{x}−\mathrm{2}\right) \\ $$$$\Rightarrow\left(\mathrm{x}−\mathrm{2}−\mathrm{1}\right)\left(\mathrm{2x}+\mathrm{7}−\mathrm{x}+\mathrm{2}\right)\leqslant\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{x}−\mathrm{3}\right)\left(\mathrm{x}+\mathrm{9}\right)\leqslant\mathrm{0}\: \\ $$$$\Rightarrow−\mathrm{9}\leqslant\mathrm{x}\leqslant\mathrm{3}\:\:\:\:\left(\mathrm{i}\right) \\ $$$$\left(\mathrm{ii}\right)\:\mathrm{2x}+\mathrm{7}>\mathrm{0}\Rightarrow\mathrm{x}>−\frac{\mathrm{7}}{\mathrm{2}} \\ $$$$\left(\mathrm{iii}\right)\mathrm{x}−\mathrm{2}>\mathrm{0}\Rightarrow\mathrm{x}>\mathrm{2} \\ $$$$\left(\mathrm{iv}\right)\mathrm{x}−\mathrm{2}\neq\mathrm{1}\Rightarrow\mathrm{x}\neq\mathrm{3} \\ $$$$\mathrm{solution}\::\:\left(\mathrm{i}\right)\cap\left(\mathrm{ii}\right)\cap\left(\mathrm{iii}\right)\cap\left(\mathrm{iv}\right) \\ $$$$\Rightarrow\:\mathrm{2}<\mathrm{x}<\mathrm{3} \\ $$

Commented by mathdanisur last updated on 13/Jul/21

$${thanks}\:{Ser} \\ $$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com