Question Number 146334 by tabata last updated on 12/Jul/21

Commented by tabata last updated on 12/Jul/21
$${help}\:{me}\:{sir}\:{questiin}\:\mathrm{1}\:{and}\:\mathrm{3} \\ $$
Answered by Olaf_Thorendsen last updated on 12/Jul/21
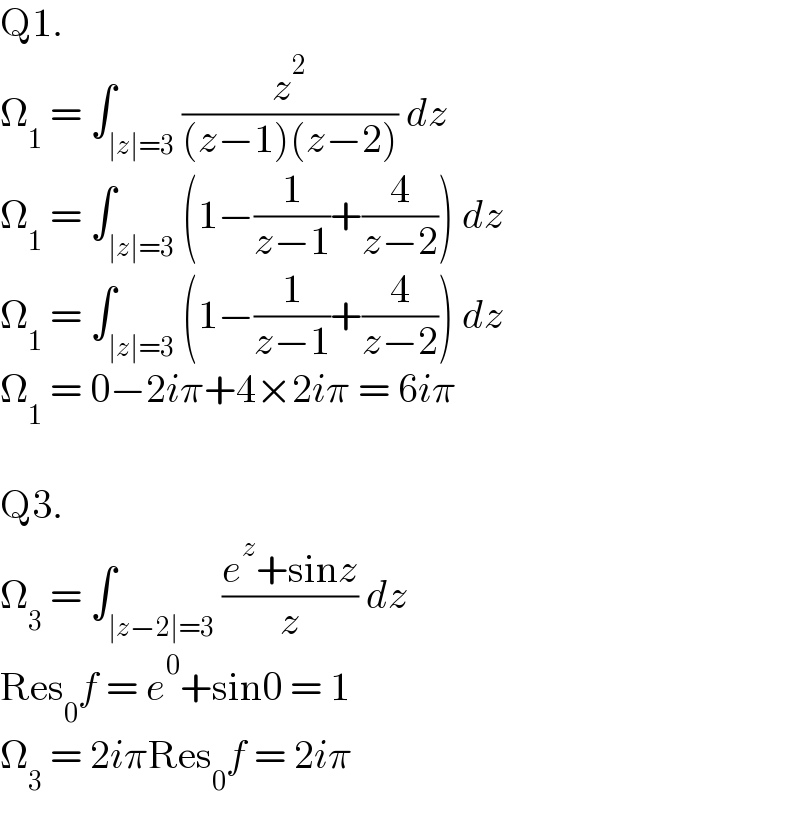
$$\mathrm{Q1}. \\ $$$$\Omega_{\mathrm{1}} \:=\:\int_{\mid{z}\mid=\mathrm{3}} \frac{{z}^{\mathrm{2}} }{\left({z}−\mathrm{1}\right)\left({z}−\mathrm{2}\right)}\:{dz} \\ $$$$\Omega_{\mathrm{1}} \:=\:\int_{\mid{z}\mid=\mathrm{3}} \left(\mathrm{1}−\frac{\mathrm{1}}{{z}−\mathrm{1}}+\frac{\mathrm{4}}{{z}−\mathrm{2}}\right)\:{dz} \\ $$$$\Omega_{\mathrm{1}} \:=\:\int_{\mid{z}\mid=\mathrm{3}} \left(\mathrm{1}−\frac{\mathrm{1}}{{z}−\mathrm{1}}+\frac{\mathrm{4}}{{z}−\mathrm{2}}\right)\:{dz} \\ $$$$\Omega_{\mathrm{1}} \:=\:\mathrm{0}−\mathrm{2}{i}\pi+\mathrm{4}×\mathrm{2}{i}\pi\:=\:\mathrm{6}{i}\pi \\ $$$$ \\ $$$$\mathrm{Q3}. \\ $$$$\Omega_{\mathrm{3}} \:=\:\int_{\mid{z}−\mathrm{2}\mid=\mathrm{3}} \frac{{e}^{{z}} +\mathrm{sin}{z}}{{z}}\:{dz} \\ $$$$\mathrm{Res}_{\mathrm{0}} {f}\:=\:{e}^{\mathrm{0}} +\mathrm{sin0}\:=\:\mathrm{1} \\ $$$$\Omega_{\mathrm{3}} \:=\:\mathrm{2}{i}\pi\mathrm{Res}_{\mathrm{0}} {f}\:=\:\mathrm{2}{i}\pi \\ $$
Answered by mathmax by abdo last updated on 13/Jul/21
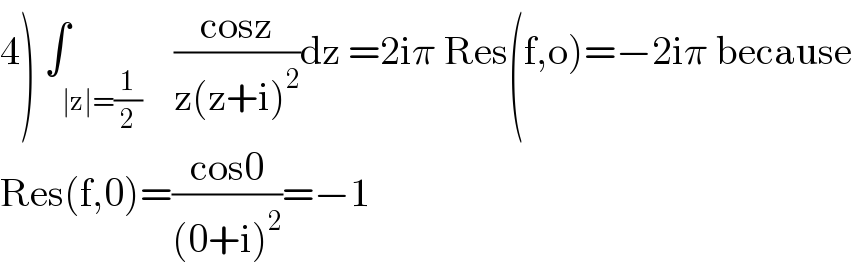
$$\left.\mathrm{4}\right)\:\int_{\mid\mathrm{z}\mid=\frac{\mathrm{1}}{\mathrm{2}}} \:\:\:\frac{\mathrm{cosz}}{\mathrm{z}\left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{2}} }\mathrm{dz}\:=\mathrm{2i}\pi\:\mathrm{Res}\left(\mathrm{f},\mathrm{o}\right)=−\mathrm{2i}\pi\:\mathrm{because} \\ $$$$\mathrm{Res}\left(\mathrm{f},\mathrm{0}\right)=\frac{\mathrm{cos0}}{\left(\mathrm{0}+\mathrm{i}\right)^{\mathrm{2}} }=−\mathrm{1} \\ $$
Answered by mathmax by abdo last updated on 13/Jul/21
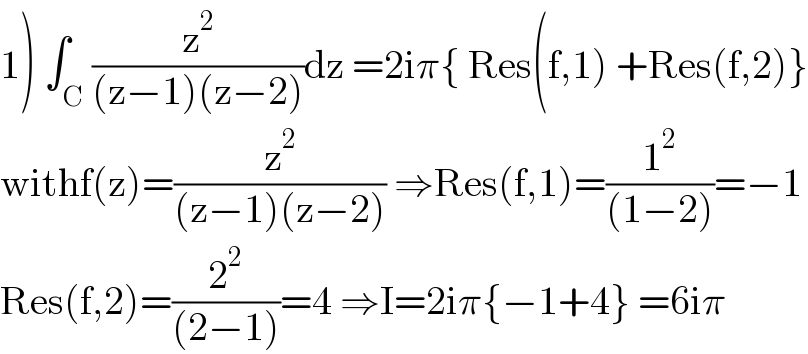
$$\left.\mathrm{1}\right)\:\int_{\mathrm{C}} \frac{\mathrm{z}^{\mathrm{2}} }{\left(\mathrm{z}−\mathrm{1}\right)\left(\mathrm{z}−\mathrm{2}\right)}\mathrm{dz}\:=\mathrm{2i}\pi\left\{\:\mathrm{Res}\left(\mathrm{f},\mathrm{1}\right)\:+\mathrm{Res}\left(\mathrm{f},\mathrm{2}\right)\right\} \\ $$$$\mathrm{withf}\left(\mathrm{z}\right)=\frac{\mathrm{z}^{\mathrm{2}} }{\left(\mathrm{z}−\mathrm{1}\right)\left(\mathrm{z}−\mathrm{2}\right)}\:\Rightarrow\mathrm{Res}\left(\mathrm{f},\mathrm{1}\right)=\frac{\mathrm{1}^{\mathrm{2}} }{\left(\mathrm{1}−\mathrm{2}\right)}=−\mathrm{1} \\ $$$$\mathrm{Res}\left(\mathrm{f},\mathrm{2}\right)=\frac{\mathrm{2}^{\mathrm{2}} }{\left(\mathrm{2}−\mathrm{1}\right)}=\mathrm{4}\:\Rightarrow\mathrm{I}=\mathrm{2i}\pi\left\{−\mathrm{1}+\mathrm{4}\right\}\:=\mathrm{6i}\pi \\ $$
Answered by mathmax by abdo last updated on 13/Jul/21
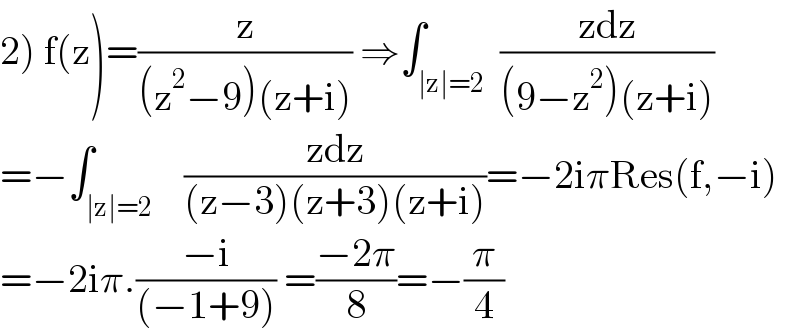
$$\left.\mathrm{2}\right)\:\mathrm{f}\left(\mathrm{z}\right)=\frac{\mathrm{z}}{\left(\mathrm{z}^{\mathrm{2}} −\mathrm{9}\right)\left(\mathrm{z}+\mathrm{i}\right)}\:\Rightarrow\int_{\mid\mathrm{z}\mid=\mathrm{2}} \:\frac{\mathrm{zdz}}{\left(\mathrm{9}−\mathrm{z}^{\mathrm{2}} \right)\left(\mathrm{z}+\mathrm{i}\right)} \\ $$$$=−\int_{\mid\mathrm{z}\mid=\mathrm{2}} \:\:\:\frac{\mathrm{zdz}}{\left(\mathrm{z}−\mathrm{3}\right)\left(\mathrm{z}+\mathrm{3}\right)\left(\mathrm{z}+\mathrm{i}\right)}=−\mathrm{2i}\pi\mathrm{Res}\left(\mathrm{f},−\mathrm{i}\right) \\ $$$$=−\mathrm{2i}\pi.\frac{−\mathrm{i}}{\left(−\mathrm{1}+\mathrm{9}\right)}\:=\frac{−\mathrm{2}\pi}{\mathrm{8}}=−\frac{\pi}{\mathrm{4}} \\ $$
Commented by Mrsof last updated on 13/Jul/21
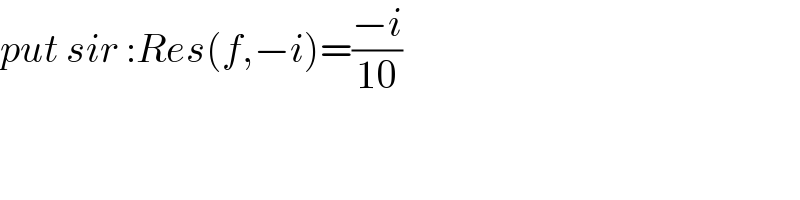
$${put}\:{sir}\::{Res}\left({f},−{i}\right)=\frac{−{i}}{\mathrm{10}} \\ $$
Answered by mathmax by abdo last updated on 13/Jul/21
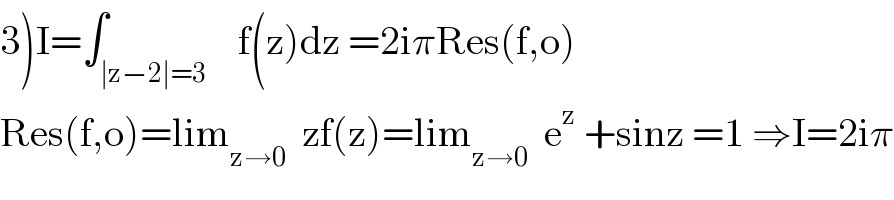
$$\left.\mathrm{3}\right)\mathrm{I}=\int_{\mid\mathrm{z}−\mathrm{2}\mid=\mathrm{3}} \:\:\:\mathrm{f}\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\mathrm{Res}\left(\mathrm{f},\mathrm{o}\right) \\ $$$$\mathrm{Res}\left(\mathrm{f},\mathrm{o}\right)=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{0}} \:\:\mathrm{zf}\left(\mathrm{z}\right)=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{0}} \:\:\mathrm{e}^{\mathrm{z}} \:+\mathrm{sinz}\:=\mathrm{1}\:\Rightarrow\mathrm{I}=\mathrm{2i}\pi \\ $$
