Question Number 146667 by puissant last updated on 14/Jul/21

Answered by Olaf_Thorendsen last updated on 14/Jul/21
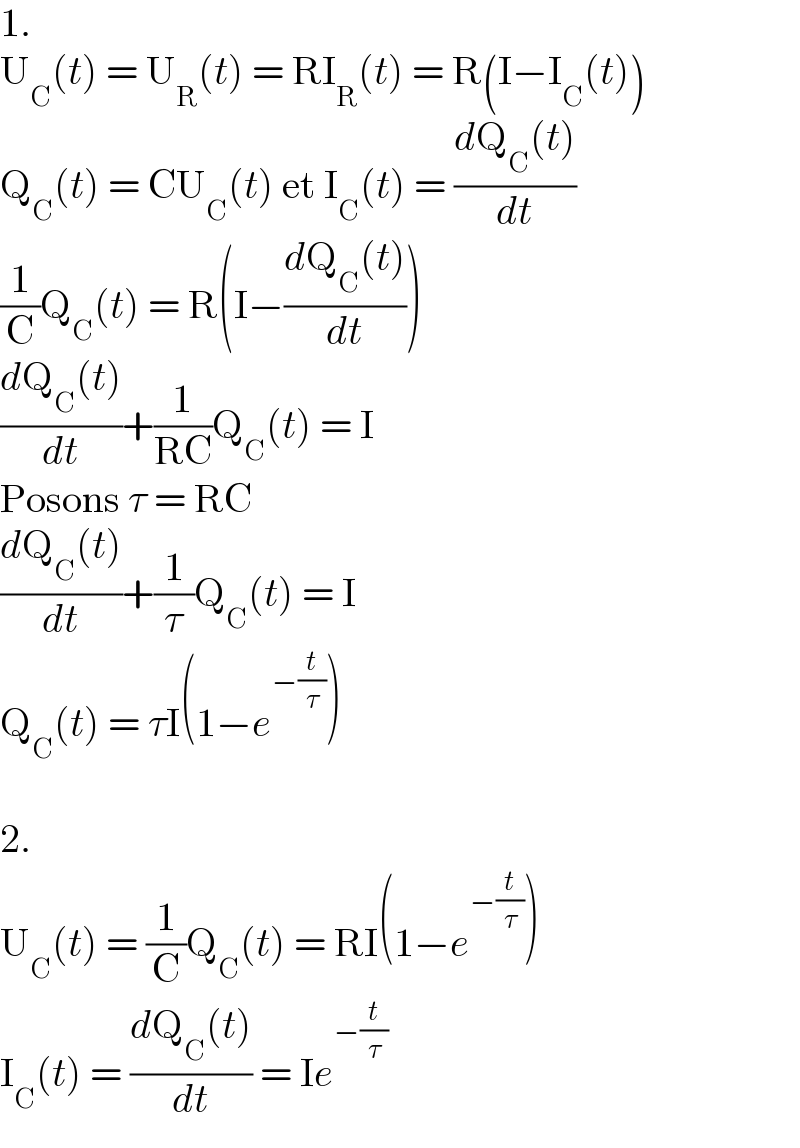
$$\mathrm{1}. \\ $$$$\mathrm{U}_{\mathrm{C}} \left({t}\right)\:=\:\mathrm{U}_{\mathrm{R}} \left({t}\right)\:=\:\mathrm{RI}_{\mathrm{R}} \left({t}\right)\:=\:\mathrm{R}\left(\mathrm{I}−\mathrm{I}_{\mathrm{C}} \left({t}\right)\right) \\ $$$$\mathrm{Q}_{\mathrm{C}} \left({t}\right)\:=\:\mathrm{CU}_{\mathrm{C}} \left({t}\right)\:\mathrm{et}\:\mathrm{I}_{\mathrm{C}} \left({t}\right)\:=\:\frac{{d}\mathrm{Q}_{\mathrm{C}} \left({t}\right)}{{dt}} \\ $$$$\frac{\mathrm{1}}{\mathrm{C}}\mathrm{Q}_{\mathrm{C}} \left({t}\right)\:=\:\mathrm{R}\left(\mathrm{I}−\frac{{d}\mathrm{Q}_{\mathrm{C}} \left({t}\right)}{{dt}}\right) \\ $$$$\frac{{d}\mathrm{Q}_{\mathrm{C}} \left({t}\right)}{{dt}}+\frac{\mathrm{1}}{\mathrm{RC}}\mathrm{Q}_{\mathrm{C}} \left({t}\right)\:=\:\mathrm{I} \\ $$$$\mathrm{Posons}\:\tau\:=\:\mathrm{RC} \\ $$$$\frac{{d}\mathrm{Q}_{\mathrm{C}} \left({t}\right)}{{dt}}+\frac{\mathrm{1}}{\tau}\mathrm{Q}_{\mathrm{C}} \left({t}\right)\:=\:\mathrm{I} \\ $$$$\mathrm{Q}_{\mathrm{C}} \left({t}\right)\:=\:\tau\mathrm{I}\left(\mathrm{1}−{e}^{−\frac{{t}}{\tau}} \right) \\ $$$$ \\ $$$$\mathrm{2}. \\ $$$$\mathrm{U}_{\mathrm{C}} \left({t}\right)\:=\:\frac{\mathrm{1}}{\mathrm{C}}\mathrm{Q}_{\mathrm{C}} \left({t}\right)\:=\:\mathrm{RI}\left(\mathrm{1}−{e}^{−\frac{{t}}{\tau}} \right) \\ $$$$\mathrm{I}_{\mathrm{C}} \left({t}\right)\:=\:\frac{{d}\mathrm{Q}_{\mathrm{C}} \left({t}\right)}{{dt}}\:=\:\mathrm{I}{e}^{−\frac{{t}}{\tau}} \\ $$
Commented by puissant last updated on 15/Jul/21

$$\mathrm{merci}\:\mathrm{monsieur} \\ $$
