Menu Close

Question-14667

Tinku Tara 0 Comments
Pin




Question Number 14667 by Umar math last updated on 03/Jun/17
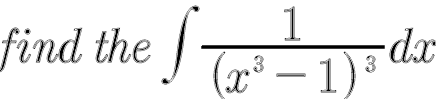
Commented by prakash jain last updated on 03/Jun/17
(1/((x^3 −1)^3 ))=(1/((x−1)^3 (x^2 +x+1)^3 )) =(A/(x−1))+(B/((x−1)^2 ))+(C/((x−1)^3 )) =((Dx+E)/(x^2 +x+1))+((Fx+G)/((x^2 +x+1)^2 ))+((Hx+I)/((x^2 +x+1)^3 )) computing (5/(27(x−1)))−(1/(9(x−1)^2 ))+(1/(27(x−1)^3 )) +((−2x−1)/(9(x^2 +x+1)^3 ))+((−7x−8)/(27(x^2 +x+1)^2 ))+((−5x−7)/(27(x^2 +x+1))) Each of the term in the partial fraction can be integrated easily. However this is a lengthy procedure.
1(x3−1)3=1(x−1)3(x2+x+1)3=Ax−1+B(x−1)2+C(x−1)3=Dx+Ex2+x+1+Fx+G(x2+x+1)2+Hx+I(x2+x+1)3computing527(x−1)−19(x−1)2+127(x−1)3+−2x−19(x2+x+1)3+−7x−827(x2+x+1)2+−5x−727(x2+x+1)Eachoftheterminthepartialfractioncanbeintegratedeasily.Howeverthisisalengthyprocedure.
Commented by Umar math last updated on 04/Jul/17
thanks sir.
thankssir.
Answered by Umar math last updated on 04/Jun/17
thank u sir
thankusir

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *