Question-146672

Question Number 146672 by mathdanisur last updated on 14/Jul/21

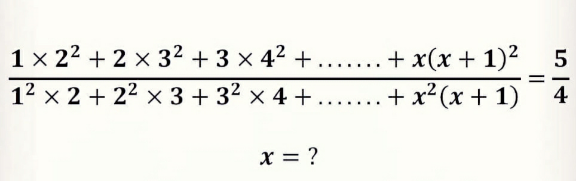
Answered by Olaf_Thorendsen last updated on 15/Jul/21

S = ((Σ_(n=1) ^x n(n+1)^2 )/(Σ_(n=1) ^x n^2 (n+1))) S = ((Σ_(n=1) ^x n^3 +2n^2 +n)/(Σ_(n=1) ^x n^3 +n^2 )) S = ((((x^2 (x+1)^2 )/4)+2.((x(x+1)(2x+1))/6)+((x(x+1))/2))/(((x^2 (x+1)^2 )/4)+((x(x+1)(2x+1))/6))) S = ((((x(x+1))/4)+(((2x+1))/3)+(1/2))/(((x(x+1))/4)+(((2x+1))/6))) S = ((3x(x+1)+4(2x+1)+6)/(3x(x+1)+2(2x+1))) S = ((3x^2 +11x+10)/(3x^2 +7x+2)) = (5/4) 12x^2 +44x+40 = 15x^2 +35x+10 3x^2 −9x−30 = 0 3(x+2)(x−5) = 0 ⇒ x = 5

$$\mathrm{S}\:=\:\frac{\underset{{n}=\mathrm{1}} {\overset{{x}} {\sum}}{n}\left({n}+\mathrm{1}\right)^{\mathrm{2}} }{\underset{{n}=\mathrm{1}} {\overset{{x}} {\sum}}{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)} \\ $$$$\mathrm{S}\:=\:\frac{\underset{{n}=\mathrm{1}} {\overset{{x}} {\sum}}{n}^{\mathrm{3}} +\mathrm{2}{n}^{\mathrm{2}} +{n}}{\underset{{n}=\mathrm{1}} {\overset{{x}} {\sum}}{n}^{\mathrm{3}} +{n}^{\mathrm{2}} } \\ $$$$\mathrm{S}\:=\:\frac{\frac{{x}^{\mathrm{2}} \left({x}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{4}}+\mathrm{2}.\frac{{x}\left({x}+\mathrm{1}\right)\left(\mathrm{2}{x}+\mathrm{1}\right)}{\mathrm{6}}+\frac{{x}\left({x}+\mathrm{1}\right)}{\mathrm{2}}}{\frac{{x}^{\mathrm{2}} \left({x}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{4}}+\frac{{x}\left({x}+\mathrm{1}\right)\left(\mathrm{2}{x}+\mathrm{1}\right)}{\mathrm{6}}} \\ $$$$\mathrm{S}\:=\:\frac{\frac{{x}\left({x}+\mathrm{1}\right)}{\mathrm{4}}+\frac{\left(\mathrm{2}{x}+\mathrm{1}\right)}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{2}}}{\frac{{x}\left({x}+\mathrm{1}\right)}{\mathrm{4}}+\frac{\left(\mathrm{2}{x}+\mathrm{1}\right)}{\mathrm{6}}} \\ $$$$\mathrm{S}\:=\:\frac{\mathrm{3}{x}\left({x}+\mathrm{1}\right)+\mathrm{4}\left(\mathrm{2}{x}+\mathrm{1}\right)+\mathrm{6}}{\mathrm{3}{x}\left({x}+\mathrm{1}\right)+\mathrm{2}\left(\mathrm{2}{x}+\mathrm{1}\right)} \\ $$$$\mathrm{S}\:=\:\frac{\mathrm{3}{x}^{\mathrm{2}} +\mathrm{11}{x}+\mathrm{10}}{\mathrm{3}{x}^{\mathrm{2}} +\mathrm{7}{x}+\mathrm{2}}\:=\:\frac{\mathrm{5}}{\mathrm{4}} \\ $$$$\mathrm{12}{x}^{\mathrm{2}} +\mathrm{44}{x}+\mathrm{40}\:=\:\mathrm{15}{x}^{\mathrm{2}} +\mathrm{35}{x}+\mathrm{10} \\ $$$$\mathrm{3}{x}^{\mathrm{2}} −\mathrm{9}{x}−\mathrm{30}\:=\:\mathrm{0} \\ $$$$\mathrm{3}\left({x}+\mathrm{2}\right)\left({x}−\mathrm{5}\right)\:=\:\mathrm{0}\:\Rightarrow\:{x}\:=\:\mathrm{5} \\ $$

Commented by mathdanisur last updated on 15/Jul/21

$${Ser},\:{ture}.? \\ $$

Commented by mathdanisur last updated on 14/Jul/21

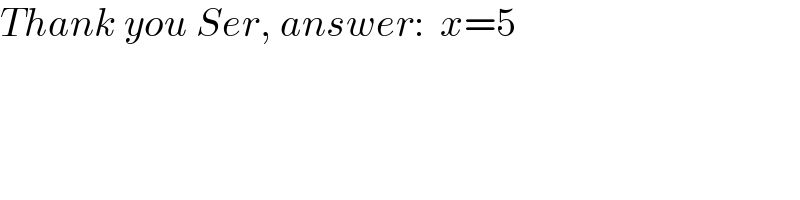
$${Thank}\:{you}\:{Ser},\:{answer}:\:\:{x}=\mathrm{5} \\ $$

Commented by bramlexs22 last updated on 15/Jul/21

$$\mathrm{your}\:\mathrm{answer}\:\mathrm{x}=\mathrm{5}\:\mathrm{is}\:\mathrm{wrong} \\ $$

Commented by som(math1967) last updated on 15/Jul/21

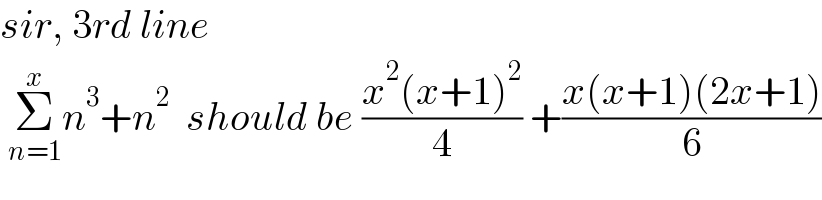
sir, 3rd line Σ_(n=1) ^x n^3 +n^2 should be ((x^2 (x+1)^2 )/4) +((x(x+1)(2x+1))/6)

$${sir},\:\mathrm{3}{rd}\:{line}\: \\ $$$$\:\underset{{n}=\mathrm{1}} {\overset{{x}} {\sum}}{n}^{\mathrm{3}} +{n}^{\mathrm{2}} \:\:{should}\:{be}\:\frac{{x}^{\mathrm{2}} \left({x}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{4}}\:+\frac{{x}\left({x}+\mathrm{1}\right)\left(\mathrm{2}{x}+\mathrm{1}\right)}{\mathrm{6}} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply